|
Bayesian Experimental Design
Bayesian experimental design provides a general probability-theoretical framework from which other theories on experimental design can be derived. It is based on Bayesian inference to interpret the observations/data acquired during the experiment. This allows accounting for both any prior knowledge on the parameters to be determined as well as uncertainties in observations. The theory of Bayesian experimental design is to a certain extent based on the theory for making optimal decisions under uncertainty. The aim when designing an experiment is to maximize the expected utility of the experiment outcome. The utility is most commonly defined in terms of a measure of the accuracy of the information provided by the experiment (e.g., the Shannon information or the negative of the variance) but may also involve factors such as the financial cost of performing the experiment. What will be the optimal experiment design depends on the particular utility criterion chosen. Relations to more ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Design Of Experiments
The design of experiments (DOE), also known as experiment design or experimental design, is the design of any task that aims to describe and explain the variation of information under conditions that are hypothesized to reflect the variation. The term is generally associated with experiments in which the design introduces conditions that directly affect the variation, but may also refer to the design of quasi-experiments, in which natural conditions that influence the variation are selected for observation. In its simplest form, an experiment aims at predicting the outcome by introducing a change of the preconditions, which is represented by one or more independent variables, also referred to as "input variables" or "predictor variables." The change in one or more independent variables is generally hypothesized to result in a change in one or more dependent variables, also referred to as "output variables" or "response variables." The experimental design may also identify ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
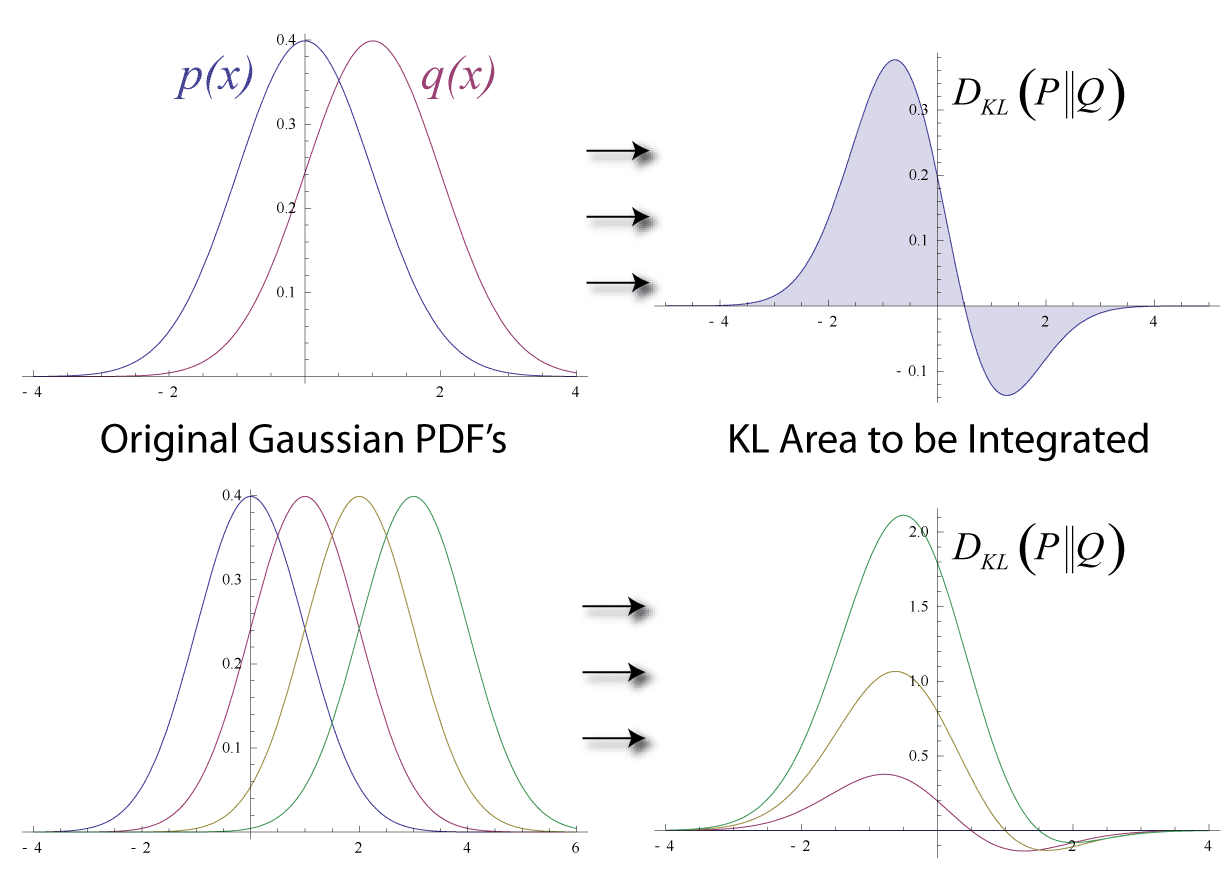
Kullback–Leibler Divergence
In mathematical statistics, the Kullback–Leibler (KL) divergence (also called relative entropy and I-divergence), denoted D_\text(P \parallel Q), is a type of statistical distance: a measure of how much a model probability distribution is different from a true probability distribution . Mathematically, it is defined as D_\text(P \parallel Q) = \sum_ P(x) \, \log \frac\text A simple interpretation of the KL divergence of from is the expected excess surprise from using as a model instead of when the actual distribution is . While it is a measure of how different two distributions are and is thus a distance in some sense, it is not actually a metric, which is the most familiar and formal type of distance. In particular, it is not symmetric in the two distributions (in contrast to variation of information), and does not satisfy the triangle inequality. Instead, in terms of information geometry, it is a type of divergence, a generalization of squared distance, and for cer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Optimal Decisions
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criteria, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries. In the more general approach, an optimization problem consists of maximizing or minimizing a real function by systematically choosing input values from within an allowed set and computing the value of the function. The generalization of optimization theory and techniques to other formulations constitutes a large area of applied mathematics. Optimization problems Optimization problems can be divided into two categories, depending on whether the variables ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Bayesian Statistics
Bayesian statistics ( or ) is a theory in the field of statistics based on the Bayesian interpretation of probability, where probability expresses a ''degree of belief'' in an event. The degree of belief may be based on prior knowledge about the event, such as the results of previous experiments, or on personal beliefs about the event. This differs from a number of other interpretations of probability, such as the frequentist interpretation, which views probability as the limit of the relative frequency of an event after many trials. More concretely, analysis in Bayesian methods codifies prior knowledge in the form of a prior distribution. Bayesian statistical methods use Bayes' theorem to compute and update probabilities after obtaining new data. Bayes' theorem describes the conditional probability of an event based on data as well as prior information or beliefs about the event or conditions related to the event. For example, in Bayesian inference, Bayes' theorem can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Calyampudi Radhakrishna Rao
Prof. Calyampudi Radhakrishna Rao (10 September 1920 – 22 August 2023) was an Indian-American mathematician and statistician. He was professor emeritus at Pennsylvania State University and research professor at the University at Buffalo. Rao was honoured by numerous colloquia, honorary degrees, and festschrifts and was awarded the US National Medal of Science in 2002. The American Statistical Association has described him as "a living legend" whose work has influenced not just statistics, but has had far reaching implications for fields as varied as economics, genetics, anthropology, geology, national planning, demography, biometry, and medicine." ''The Times of India'' listed Rao as one of the top 10 Indian scientists of all time. In 2023, Rao was awarded the International Prize in Statistics, an award often touted as the "statistics' equivalent of the Nobel Prize". Rao was also a Senior Policy and Statistics advisor for the Indian Heart Association non-profit focused on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |