|
Baker's Method
In transcendental number theory, a mathematical discipline, Baker's theorem gives a lower bound for the absolute value of linear combinations of logarithms of algebraic numbers. The result, proved by , subsumed many earlier results in transcendental number theory and solved a problem posed by Alexander Gelfond nearly fifteen years earlier. Baker used this to prove the transcendence of many numbers, to derive effective bounds for the solutions of some Diophantine equations, and to solve the class number problem of finding all imaginary quadratic fields with class number 1. History To simplify notation, let \mathbb be the set of logarithms to the base ''e'' of nonzero algebraic numbers, that is \mathbb = \left \, where \Complex denotes the set of complex numbers and \overline denotes the algebraic numbers (the algebraic completion of the rational numbers \Q). Using this notation, several results in transcendental number theory become much easier to state. For example the HermiteÔ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transcendental Number Theory
Transcendental number theory is a branch of number theory that investigates transcendental numbers (numbers that are not solutions of any polynomial equation with rational coefficients), in both qualitative and quantitative ways. Transcendence The fundamental theorem of algebra tells us that if we have a non-constant polynomial with rational coefficients (or equivalently, by clearing denominators, with integer coefficients) then that polynomial will have a root in the complex numbers. That is, for any non-constant polynomial P with rational coefficients there will be a complex number \alpha such that P(\alpha)=0. Transcendence theory is concerned with the converse question: given a complex number \alpha, is there a polynomial P with rational coefficients such that P(\alpha)=0? If no such polynomial exists then the number is called transcendental. More generally the theory deals with algebraic independence of numbers. A set of numbers is called algebraically independent o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gisbert W├╝stholz
Gisbert W├╝stholz (born June 4, 1948, in Tuttlingen, Germany) is a German mathematician internationally known for his fundamental contributions to number theory (in the field of transcendental number theory, Diophantine approximation) and arithmetic geometry. Education, Career and Research Gisbert W├╝stholz was born in 1948 in Tuttlingen (Baden-W├╝rttemberg) and studied from 1967 to 1973 at the University of Freiburg where he finished his PhD under the supervision of Theodor Schneider in 1978. On the invitation of Friedrich Hirzebruch he stayed for a year as a Postdoc at the University of Bonn and then he got a Postdoc position at the University of Wuppertal where he worked with Walter Borho from 1979 till 1984 and then moved to Bonn to become associate professor at the newly founded Max Planck Institute for Mathematics. From 1985 to 1987 he was full Professor for Mathematics at Wuppertal and in 1987 elected for a chair in Mathematics at ETH Zurich. He founded the Zurich Graduate S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leopoldt's Conjecture
In algebraic number theory, Leopoldt's conjecture, introduced by , states that the p-adic regulator of a number field does not vanish. The p-adic regulator is an analogue of the usual regulator defined using p-adic logarithms instead of the usual logarithms, introduced by . Leopoldt proposed a definition of a p-adic regulator ''R''''p'' attached to ''K'' and a prime number ''p''. The definition of ''R''''p'' uses an appropriate determinant with entries the p-adic logarithm of a generating set of units of ''K'' (up to torsion), in the manner of the usual regulator. The conjecture, which for general ''K'' is still open , then comes out as the statement that ''R''''p'' is not zero. Formulation Let ''K'' be a number field and for each prime ''P'' of ''K'' above some fixed rational prime ''p'', let ''U''''P'' denote the local units at ''P'' and let ''U''1,''P'' denote the subgroup of principal units in ''U''''P''. Set : U_1 = \prod_ U_. Then let ''E''1 denote the set of global ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
P-adic Exponential Function
In mathematics, the -adic number system for any prime number extends the ordinary arithmetic of the rational numbers in a different way from the extension of the rational number system to the real and complex number systems. The extension is achieved by an alternative interpretation of the concept of "closeness" or absolute value. In particular, two -adic numbers are considered to be close when their difference is divisible by a high power of : the higher the power, the closer they are. This property enables -adic numbers to encode congruence information in a way that turns out to have powerful applications in number theory ÔÇô including, for example, in the famous proof of Fermat's Last Theorem by Andrew Wiles. These numbers were first described by Kurt Hensel in 1897, though, with hindsight, some of Ernst Kummer's earlier work can be interpreted as implicitly using -adic numbers.Translator's introductionpage 35 "Indeed, with hindsight it becomes apparent that a discret ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
P-adic
In mathematics, the -adic number system for any prime number extends the ordinary arithmetic of the rational numbers in a different way from the extension of the rational number system to the real and complex number systems. The extension is achieved by an alternative interpretation of the concept of "closeness" or absolute value. In particular, two -adic numbers are considered to be close when their difference is divisible by a high power of : the higher the power, the closer they are. This property enables -adic numbers to encode congruence information in a way that turns out to have powerful applications in number theory ÔÇô including, for example, in the famous proof of Fermat's Last Theorem by Andrew Wiles. These numbers were first described by Kurt Hensel in 1897, though, with hindsight, some of Ernst Kummer's earlier work can be interpreted as implicitly using -adic numbers.Translator's introductionpage 35 "Indeed, with hindsight it becomes apparent that a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homogeneous Polynomial
In mathematics, a homogeneous polynomial, sometimes called quantic in older texts, is a polynomial whose nonzero terms all have the same degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial of degree 5, in two variables; the sum of the exponents in each term is always 5. The polynomial x^3 + 3 x^2 y + z^7 is not homogeneous, because the sum of exponents does not match from term to term. The function defined by a homogeneous polynomial is always a homogeneous function. An algebraic form, or simply form, is a function defined by a homogeneous polynomial. A binary form is a form in two variables. A ''form'' is also a function defined on a vector space, which may be expressed as a homogeneous function of the coordinates over any basis. A polynomial of degree 0 is always homogeneous; it is simply an element of the field or ring of the coefficients, usually called a constant or a scalar. A form of degree 1 is a linear form. A form of degree 2 is a quadra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Independence
In abstract algebra, a subset S of a field L is algebraically independent over a subfield K if the elements of S do not satisfy any non-trivial polynomial equation with coefficients in K. In particular, a one element set \ is algebraically independent over K if and only if \alpha is transcendental over K. In general, all the elements of an algebraically independent set S over K are by necessity transcendental over K, and over all of the field extensions over K generated by the remaining elements of S. Example The two real numbers \sqrt and 2\pi+1 are each transcendental numbers: they are not the roots of any nontrivial polynomial whose coefficients are rational numbers. Thus, each of the two singleton sets \ and \ are algebraically independent over the field \mathbb of rational numbers. However, the set \ is ''not'' algebraically independent over the rational numbers, because the nontrivial polynomial :P(x,y)=2x^2-y+1 is zero when x=\sqrt and y=2\pi+1. Algebraic independenc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
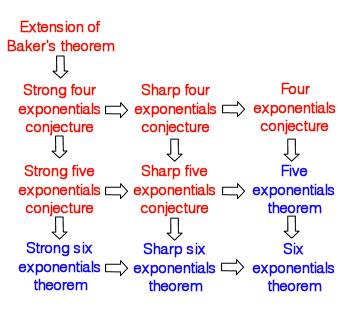
Four Exponentials Conjecture
In mathematics, specifically the field of transcendental number theory, the four exponentials conjecture is a conjecture which, given the right conditions on the exponents, would guarantee the transcendence of at least one of four exponentials. The conjecture, along with two related, stronger conjectures, is at the top of a hierarchy of conjectures and theorems concerning the arithmetic nature of a certain number of values of the exponential function. Statement If ''x''1, ''x''2 and ''y''1, ''y''2 are two pairs of complex numbers, with each pair being linearly independent over the rational numbers, then at least one of the following four numbers is transcendental: :e^, e^, e^, e^. An alternative way of stating the conjecture in terms of logarithms is the following. For 1 ≤ ''i'', ''j'' ≤ 2 let ╬╗''ij'' be complex numbers such that exp(╬╗''ij'') are all algebraic. Suppose ╬╗11 and ╬╗12 are linearly independent over the rational numbers, and ╬╗11 and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Six Exponentials Theorem
In mathematics, specifically transcendental number theory, the six exponentials theorem is a result that, given the right conditions on the exponents, guarantees the transcendence of at least one of a set of exponentials. Statement If ''x''1, ''x''2, ..., ''x''''d'' are ''d'' complex numbers that are linearly independent over the rational numbers, and ''y''1, ''y''2, ..., ''y''''l'' are ''l'' complex numbers that are also linearly independent over the rational numbers, and if ''dl'' > ''d'' + ''l'', then at least one of the following ''dl'' numbers is transcendental: :\exp(x_i y_j),\quad (1 \leq i \leq d,\ 1 \leq j \leq l). The most interesting case is when ''d'' = 3 and ''l'' = 2, in which case there are six exponentials, hence the name of the result. The theorem is weaker than the related but thus far unproved four exponentials conjecture, whereby the strict inequality ''dl'' > ''d'' + ''l'' is replaced with ''dl' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schanuel's Conjecture
In mathematics, specifically transcendental number theory, Schanuel's conjecture is a conjecture made by Stephen Schanuel in the 1960s concerning the transcendence degree of certain field extensions of the rational numbers. Statement The conjecture is as follows: :Given any complex numbers that are linearly independent over the rational numbers \mathbb, the field extension \mathbb(''z''1, ..., ''z''''n'', ''e''''z''1, ..., ''e''''z''''n'') has transcendence degree at least over \mathbb. The conjecture can be found in Lang (1966). Consequences The conjecture, if proven, would generalize most known results in transcendental number theory. The special case where the numbers ''z''1,...,''z''''n'' are all algebraic is the LindemannÔÇôWeierstrass theorem. If, on the other hand, the numbers are chosen so as to make exp(''z''1),...,exp(''z''''n'') all algebraic then one would prove that linearly independent logarithms of algebraic numbers are algebraically independent, a st ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vandermonde Matrix
In linear algebra, a Vandermonde matrix, named after Alexandre-Th├ęophile Vandermonde, is a matrix with the terms of a geometric progression in each row: an matrix :V=\begin 1 & x_1 & x_1^2 & \dots & x_1^\\ 1 & x_2 & x_2^2 & \dots & x_2^\\ 1 & x_3 & x_3^2 & \dots & x_3^\\ \vdots & \vdots & \vdots & \ddots &\vdots \\ 1 & x_m & x_m^2 & \dots & x_m^ \end, or :V_ = x_i^ \, for all indices and . Some authors define the Vandermonde matrix as the transpose of the above matrix. The determinant of a square Vandermonde matrix is called a '' Vandermonde polynomial'' or ''Vandermonde determinant''. Its value is the polynomial :\det(V) = \prod_ (x_j - x_i) which is non-zero if and only if all x_i are distinct. The Vandermonde determinant was sometimes called the ''discriminant'', although, presently, the discriminant of a polynomial is the square of the Vandermonde determinant of the roots of the polynomial. The Vandermonde determinant is an alternating form in the x_i, meaning that excha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Siegel's Lemma
In mathematics, specifically in transcendental number theory and Diophantine approximation, Siegel's lemma refers to bounds on the solutions of linear equations obtained by the construction of auxiliary functions. The existence of these polynomials was proven by Axel Thue; Thue's proof used Dirichlet's box principle. Carl Ludwig Siegel published his lemma in 1929. It is a pure existence theorem for a system of linear equations. Siegel's lemma has been refined in recent years to produce sharper bounds on the estimates given by the lemma. Statement Suppose we are given a system of ''M'' linear equations in ''N'' unknowns such that ''N'' > ''M'', say :a_ X_1 + \cdots+ a_ X_N = 0 :\cdots :a_ X_1 +\cdots+ a_ X_N = 0 where the coefficients are rational integers, not all 0, and bounded by ''B''. The system then has a solution :(X_1, X_2, \dots, X_N) with the ''X''s all rational integers, not all 0, and bounded by :(NB)^. Lemma D.4.1, page 316. gave the following sharper bound fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |