Four Exponentials Conjecture on:
[Wikipedia]
[Google]
[Amazon]
In mathematics, specifically the field of
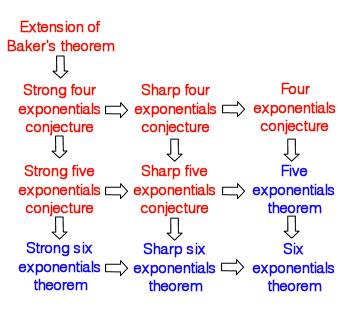 The strongest result that has been conjectured in this circle of problems is the strong four exponentials conjecture. This result would imply both aforementioned conjectures concerning four exponentials as well as all the five and six exponentials conjectures and theorems, as illustrated to the right, and all the three exponentials conjectures detailed below. The statement of this conjecture deals with the
The strongest result that has been conjectured in this circle of problems is the strong four exponentials conjecture. This result would imply both aforementioned conjectures concerning four exponentials as well as all the five and six exponentials conjectures and theorems, as illustrated to the right, and all the three exponentials conjectures detailed below. The statement of this conjecture deals with the
transcendental number theory
Transcendental number theory is a branch of number theory that investigates transcendental numbers (numbers that are not solutions of any polynomial equation with rational coefficients), in both qualitative and quantitative ways.
Transcendence
...
, the four exponentials conjecture is a conjecture
In mathematics, a conjecture is a conclusion or a proposition that is proffered on a tentative basis without proof. Some conjectures, such as the Riemann hypothesis (still a conjecture) or Fermat's Last Theorem (a conjecture until proven in 1 ...
which, given the right conditions on the exponents, would guarantee the transcendence
Transcendence, transcendent, or transcendental may refer to:
Mathematics
* Transcendental number, a number that is not the root of any polynomial with rational coefficients
* Algebraic element or transcendental element, an element of a field exten ...
of at least one of four exponentials. The conjecture, along with two related, stronger conjectures, is at the top of a hierarchy of conjectures and theorems concerning the arithmetic nature of a certain number of values of the exponential function
The exponential function is a mathematical function denoted by f(x)=\exp(x) or e^x (where the argument is written as an exponent). Unless otherwise specified, the term generally refers to the positive-valued function of a real variable, ...
.
Statement
If ''x''1, ''x''2 and ''y''1, ''y''2 are two pairs ofcomplex numbers
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
, with each pair being linearly independent
In the theory of vector spaces, a set of vectors is said to be if there is a nontrivial linear combination of the vectors that equals the zero vector. If no such linear combination exists, then the vectors are said to be . These concepts ...
over the rational numbers
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (e.g. ). The set of all r ...
, then at least one of the following four numbers is transcendental
Transcendence, transcendent, or transcendental may refer to:
Mathematics
* Transcendental number, a number that is not the root of any polynomial with rational coefficients
* Algebraic element or transcendental element, an element of a field exten ...
:
:
An alternative way of stating the conjecture in terms of logarithms is the following. For 1 ≤ ''i'', ''j'' ≤ 2 let λ''ij'' be complex numbers such that exp(λ''ij'') are all algebraic. Suppose λ11 and λ12 are linearly independent over the rational numbers, and λ11 and λ21 are also linearly independent over the rational numbers, then
:
An equivalent formulation in terms of linear algebra
Linear algebra is the branch of mathematics concerning linear equations such as:
:a_1x_1+\cdots +a_nx_n=b,
linear maps such as:
:(x_1, \ldots, x_n) \mapsto a_1x_1+\cdots +a_nx_n,
and their representations in vector spaces and through matric ...
is the following. Let ''M'' be the 2×2 matrix
Matrix most commonly refers to:
* ''The Matrix'' (franchise), an American media franchise
** '' The Matrix'', a 1999 science-fiction action film
** "The Matrix", a fictional setting, a virtual reality environment, within ''The Matrix'' (franchi ...
:
where exp(λ''ij'') is algebraic for 1 ≤ ''i'', ''j'' ≤ 2. Suppose the two rows of ''M'' are linearly independent over the rational numbers, and the two columns of ''M'' are linearly independent over the rational numbers. Then the rank
Rank is the relative position, value, worth, complexity, power, importance, authority, level, etc. of a person or object within a ranking, such as:
Level or position in a hierarchical organization
* Academic rank
* Diplomatic rank
* Hierarchy
* H ...
of ''M'' is 2.
While a 2×2 matrix having linearly independent rows and columns usually means it has rank 2, in this case we require linear independence over a smaller field so the rank isn't forced to be 2. For example, the matrix
:
has rows and columns that are linearly independent over the rational numbers, since ''π'' is irrational
Irrationality is cognition, thinking, talking, or acting without inclusion of rationality. It is more specifically described as an action or opinion given through inadequate use of reason, or through emotional distress or cognitive deficiency. ...
. But the rank of the matrix is 1. So in this case the conjecture would imply that at least one of ''e'', ''e''''π'', and ''e''''π''2 is transcendental (which in this case is already known since ''e'' is transcendental).
History
The conjecture was considered in the early 1940s byAtle Selberg
Atle Selberg (14 June 1917 – 6 August 2007) was a Norwegian mathematician known for his work in analytic number theory and the theory of automorphic forms, and in particular for bringing them into relation with spectral theory. He was awarded ...
who never formally stated the conjecture. A special case of the conjecture is mentioned in a 1944 paper of Leonidas Alaoglu
Leonidas (''Leon'') Alaoglu ( el, Λεωνίδας Αλάογλου; March 19, 1914 – August 1981) was a mathematician, known for his result, called Alaoglu's theorem on the weak-star compactness of the closed unit ball in the dual of a n ...
and Paul Erdős who suggest that it had been considered by Carl Ludwig Siegel
Carl Ludwig Siegel (31 December 1896 – 4 April 1981) was a German mathematician specialising in analytic number theory. He is known for, amongst other things, his contributions to the Thue–Siegel–Roth theorem in Diophantine approximation ...
. An equivalent statement was first mentioned in print by Theodor Schneider __NOTOC__
Theodor Schneider (7 May 1911, Frankfurt am Main – 31 October 1988, Freiburg im Breisgau) was a German mathematician, best known for providing proof of what is now known as the Gelfond–Schneider theorem.
Schneider studied from 19 ...
who set it as the first of eight important, open problems in transcendental number theory in 1957.
The related six exponentials theorem
In mathematics, specifically transcendental number theory, the six exponentials theorem is a result that, given the right conditions on the exponents, guarantees the transcendence of at least one of a set of exponentials.
Statement
If ''x''1, '' ...
was first explicitly mentioned in the 1960s by Serge Lang
Serge Lang (; May 19, 1927 – September 12, 2005) was a French-American mathematician and activist who taught at Yale University for most of his career. He is known for his work in number theory and for his mathematics textbooks, including the i ...
and Kanakanahalli Ramachandra
Kanakanahalli Ramachandra (18 August 1933 – 17 January 2011) was an Indian mathematician working in both analytic number theory and algebraic number theory.
Early career
After his father's death at age 13, he had to look for a job. Ramachan ...
, and both also explicitly conjecture the above result. Indeed, after proving the six exponentials theorem Lang mentions the difficulty in dropping the number of exponents from six to four — the proof used for six exponentials "just misses" when one tries to apply it to four.
Corollaries
UsingEuler's identity
In mathematics, Euler's identity (also known as Euler's equation) is the equality
e^ + 1 = 0
where
: is Euler's number, the base of natural logarithms,
: is the imaginary unit, which by definition satisfies , and
: is pi, the ratio of the circ ...
this conjecture implies the transcendence of many numbers involving ''e'' and π. For example, taking ''x''1 = 1, ''x''2 = , ''y''1 = ''iπ'', and ''y''2 = ''iπ'', the conjecture—if true—implies that one of the following four numbers is transcendental:
:
The first of these is just −1, and the fourth is 1, so the conjecture implies that ''e''''iπ'' is transcendental (which is already known, by consequence of the Gelfond–Schneider theorem
In mathematics, the Gelfond–Schneider theorem establishes the transcendence of a large class of numbers.
History
It was originally proved independently in 1934 by Aleksandr Gelfond and Theodor Schneider.
Statement
: If ''a'' and ''b'' ar ...
).
An open problem in number theory
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and integer-valued functions. German mathematician Carl Friedrich Gauss (1777–1855) said, "Math ...
settled by the conjecture is the question of whether there exists a non-integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign ( −1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language ...
real number
In mathematics, a real number is a number that can be used to measurement, measure a ''continuous'' one-dimensional quantity such as a distance, time, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small var ...
''t'' such that both 2''t'' and 3''t'' are integers, or indeed such that ''a''''t'' and ''b''''t'' are both integers for some pair of integers ''a'' and ''b'' that are multiplicatively independent over the integers. Values of ''t'' such that 2''t'' is an integer are all of the form ''t'' = log2''m'' for some integer ''m'', while for 3''t'' to be an integer, ''t'' must be of the form ''t'' = log3''n'' for some integer ''n''. By setting ''x''1 = 1, ''x''2 = ''t'', ''y''1 = log(2), and ''y''2 = log(3), the four exponentials conjecture implies that if ''t'' is irrational then one of the following four numbers is transcendental:
:
So if 2''t'' and 3''t'' are both integers then the conjecture implies that ''t'' must be a rational number. Since the only rational numbers ''t'' for which 2''t'' is also rational are the integers, this implies that there are no non-integer real numbers ''t'' such that both 2''t'' and 3''t'' are integers. It is this consequence, for any two primes
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways ...
(not just 2 and 3), that Alaoglu and Erdős desired in their paper as it would imply the conjecture that the quotient of two consecutive colossally abundant number
In mathematics, a colossally abundant number (sometimes abbreviated as CA) is a natural number that, in a particular, rigorous sense, has many divisors. Formally, a number ''n'' is said to be colossally abundant if there is an ε > 0 s ...
s is prime, extending Ramanujan's results on the quotients of consecutive superior highly composite number
In mathematics, a superior highly composite number is a natural number which has the highest ratio of its number of divisors to ''some'' positive power of itself than any other number. It is a stronger restriction than that of a highly composit ...
.
Sharp four exponentials conjecture
The four exponentials conjecture reduces the pair and triplet of complex numbers in the hypotheses of the six exponentials theorem to two pairs. It is conjectured that this is also possible with the sharp six exponentials theorem, and this is the sharp four exponentials conjecture. Specifically, this conjecture claims that if ''x''1, ''x''2, and ''y''1, ''y''2 are two pairs of complex numbers with each pair being linearly independent over the rational numbers, and if β''ij'' are four algebraic numbers for 1 ≤ ''i'', ''j'' ≤ 2 such that the following four numbers are algebraic: : then ''x''''i'' ''y''''j'' = β''ij'' for 1 ≤ ''i'', ''j'' ≤ 2. So all four exponentials are in fact 1. This conjecture implies both the sharp six exponentials theorem, which requires a third ''x'' value, and the as yet unproven sharp five exponentials conjecture that requires a further exponential to be algebraic in its hypotheses.Strong four exponentials conjecture
 The strongest result that has been conjectured in this circle of problems is the strong four exponentials conjecture. This result would imply both aforementioned conjectures concerning four exponentials as well as all the five and six exponentials conjectures and theorems, as illustrated to the right, and all the three exponentials conjectures detailed below. The statement of this conjecture deals with the
The strongest result that has been conjectured in this circle of problems is the strong four exponentials conjecture. This result would imply both aforementioned conjectures concerning four exponentials as well as all the five and six exponentials conjectures and theorems, as illustrated to the right, and all the three exponentials conjectures detailed below. The statement of this conjecture deals with the vector space
In mathematics and physics, a vector space (also called a linear space) is a set whose elements, often called '' vectors'', may be added together and multiplied ("scaled") by numbers called '' scalars''. Scalars are often real numbers, but ...
over the algebraic numbers generated by 1 and all logarithms of non-zero algebraic numbers, denoted here as ''L''∗. So ''L''∗ is the set of all complex numbers of the form
:
for some ''n'' ≥ 0, where all the β''i'' and α''i'' are algebraic and every branch of the logarithm is considered. The statement of the strong four exponentials conjecture is then as follows. Let ''x''1, ''x''2, and ''y''1, ''y''2 be two pairs of complex numbers with each pair being linearly independent over the algebraic numbers, then at least one of the four numbers ''x''''i'' ''y''''j'' for 1 ≤ ''i'', ''j'' ≤ 2 is not in ''L''∗.
Three exponentials conjecture
The four exponentials conjecture rules out a special case of non-trivial,homogeneous
Homogeneity and heterogeneity are concepts often used in the sciences and statistics relating to the uniformity of a substance or organism. A material or image that is homogeneous is uniform in composition or character (i.e. color, shape, siz ...
, quadratic relations between logarithms of algebraic numbers. But a conjectural extension of Baker's theorem
In transcendental number theory, a mathematical discipline, Baker's theorem gives a lower bound for the absolute value of linear combinations of logarithms of algebraic numbers. The result, proved by , subsumed many earlier results in transcendenta ...
implies that there should be no non-trivial algebraic relations between logarithms of algebraic numbers at all, homogeneous or not. One case of non-homogeneous quadratic relations is covered by the still open three exponentials conjecture. In its logarithmic form it is the following conjecture. Let λ1, λ2, and λ3 be any three logarithms of algebraic numbers and γ be a non-zero algebraic number, and suppose that λ1λ2 = γλ3. Then λ1λ2 = γλ3 = 0.
The exponential form of this conjecture is the following. Let ''x''1, ''x''2, and ''y'' be non-zero complex numbers and let γ be a non-zero algebraic number. Then at least one of the following three numbers is transcendental:
:
There is also a sharp three exponentials conjecture which claims that if ''x''1, ''x''2, and ''y'' are non-zero complex numbers and α, β1, β2, and γ are algebraic numbers such that the following three numbers are algebraic
:
then either ''x''2''y'' = β2 or γ''x''1 = α''x''2.
The strong three exponentials conjecture meanwhile states that if ''x''1, ''x''2, and ''y'' are non-zero complex numbers with ''x''1''y'', ''x''2''y'', and ''x''1/''x''2 all transcendental, then at least one of the three numbers ''x''1''y'', ''x''2''y'', ''x''1/''x''2 is not in ''L''∗.
As with the other results in this family, the strong three exponentials conjecture implies the sharp three exponentials conjecture which implies the three exponentials conjecture. However, the strong and sharp three exponentials conjectures are implied by their four exponentials counterparts, bucking the usual trend. And the three exponentials conjecture is neither implied by nor implies the four exponentials conjecture.
The three exponentials conjecture, like the sharp five exponentials conjecture, would imply the transcendence of ''e''π2 by letting (in the logarithmic version) λ1 = ''i''π, λ2 = −''i''π, and γ = 1.
Bertrand's conjecture
Many of the theorems and results in transcendental number theory concerning the exponential function have analogues involving the modular function ''j''. Writing ''q'' = ''e''2π''i'' for the nome and ''j''() = ''J''(''q''), Daniel Bertrand conjectured that if ''q''1 and ''q''2 are non-zero algebraic numbers in the complexunit disc
In mathematics, the open unit disk (or disc) around ''P'' (where ''P'' is a given point in the plane), is the set of points whose distance from ''P'' is less than 1:
:D_1(P) = \.\,
The closed unit disk around ''P'' is the set of points whose ...
that are multiplicatively independent, then ''J''(''q''1) and ''J''(''q''2) are algebraically independent over the rational numbers. Although not obviously related to the four exponentials conjecture, Bertrand's conjecture in fact implies a special case known as the weak four exponentials conjecture.Diaz, (2001), section 4. This conjecture states that if ''x''1 and ''x''2 are two positive real algebraic numbers, neither of them equal to 1, then π2 and the product are linearly independent over the rational numbers. This corresponds to the special case of the four exponentials conjecture whereby ''y''1 = ''i''π, ''y''2 = −''i''π, and ''x''1 and ''x''2 are real. Perhaps surprisingly, though, it is also a corollary of Bertrand's conjecture, suggesting there may be an approach to the full four exponentials conjecture via the modular function ''j''.
Notes
References
* * * * * * * * * * *External links
* *{{MathWorld, urlname=FourExponentialsConjecture, title=Four Exponentials Conjecture Conjectures Transcendental numbers Exponentials Unsolved problems in number theory