|
Brillouin's Theorem
In quantum chemistry, Brillouin's theorem, proposed by the French physicist Léon Brillouin in 1934, relates to Hartree–Fock wavefunctions. Hartree–Fock, or the self-consistent field method, is a non- relativistic method of generating approximate wavefunctions for a many-bodied quantum system, based on the assumption that each electron is exposed to an average of the positions of all other electrons, and that the solution is a linear combination of pre-specified basis functions. The theorem states that given a self-consistent optimized Hartree–Fock wavefunction , \psi_0\rangle, the matrix element of the Hamiltonian between the ground state and a single excited determinant (i.e. one where an occupied orbital ''a'' is replaced by a virtual orbital ''r'') must be zero. \langle \psi_0, \hat , \psi_a^r \rangle =0 This theorem is important in constructing a configuration interaction method, among other applications. Another interpretation of the theorem is that the ground elect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Chemistry
Quantum chemistry, also called molecular quantum mechanics, is a branch of physical chemistry focused on the application of quantum mechanics to chemical systems, particularly towards the quantum-mechanical calculation of electronic contributions to physical and chemical properties of Molecule, molecules, Material, materials, and solutions at the atomic level. These calculations include systematically applied approximations intended to make calculations computationally feasible while still capturing as much information about important contributions to the computed Wave function, wave functions as well as to observable properties such as structures, spectra, and Thermodynamics, thermodynamic properties. Quantum chemistry is also concerned with the computation of quantum effects on molecular dynamics and chemical kinetics. Chemists rely heavily on spectroscopy through which information regarding the Quantization (physics), quantization of energy on a molecular scale can be obtained ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electron Correlation
Electronic correlation is the interaction between electrons in the electronic structure of a quantum system. The correlation energy is a measure of how much the movement of one electron is influenced by the presence of all other electrons. Atomic and molecular systems Within the Hartree–Fock method of quantum chemistry, the antisymmetric wave function is approximated by a single Slater determinant. Exact wave functions, however, cannot generally be expressed as single determinants. The single-determinant approximation does not take into account Coulomb correlation, leading to a total electronic energy different from the exact solution of the non-relativistic Schrödinger equation within the Born–Oppenheimer approximation. Therefore, the Hartree–Fock limit is always above this exact energy. The difference is called the ''correlation energy'', a term coined by Löwdin. The concept of the correlation energy was studied earlier by Wigner. A certain amount of electr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variational Principle
A variational principle is a mathematical procedure that renders a physical problem solvable by the calculus of variations, which concerns finding functions that optimize the values of quantities that depend on those functions. For example, the problem of determining the shape of a hanging chain suspended at both ends—a catenary—can be solved using variational calculus, and in this case, the variational principle is the following: The solution is a function that minimizes the gravitational potential energy of the chain. History Physics The history of the variational principle in classical mechanics started with Maupertuis's principle in the 18th century. Math Felix Klein's 1872 Erlangen program attempted to identify invariants under a group of transformations. Examples In mathematics * Ekeland's variational principle in mathematical optimization * The finite element method * The variation principle relating topological entropy and Kolmogorov-Sinai entropy. In physics * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Self Consistent Field
In philosophy, the self is an individual's own being, knowledge, and values, and the relationship between these attributes. The first-person perspective distinguishes selfhood from personal identity. Whereas "identity" is (literally) sameness and may involve categorization and labeling, selfhood implies a first-person perspective and suggests potential uniqueness. Conversely, "person" is used as a third-person reference. Personal identity can be impaired in late-stage Alzheimer's disease and in other neurodegenerative diseases. Finally, the self is distinguishable from "others". Including the distinction between sameness and otherness, the self versus other is a research topic in contemporary philosophy and contemporary phenomenology (see also psychological phenomenology), psychology, psychiatry, neurology, and neuroscience. Although subjective experience is central to selfhood, the privacy of this experience is only one of many problems in the philosophy of self and scie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fock Matrix
The Fock matrix is defined by the Fock operator. In its general form the Fock operator writes: :\hat F(i) = \hat h(i)+\sum_^ hat J_j(i)-\hat K_j(i)/math> Where ''i'' runs over the total ''N'' spin orbitals. In the closed-shell case, it can be simplified by considering only the spatial orbitals. Noting that the \hat J terms are duplicated and the exchange terms are null between different spins. For the restricted case which assumes closed-shell orbitals and single- determinantal wavefunctions, the Fock operator for the ''i''-th electron is given by:Levine, I.N. (1991) ''Quantum Chemistry'' (4th ed., Prentice-Hall), p.403 :\hat F(i) = \hat h(i)+\sum_^ \hat J_j(i)-\hat K_j(i)/math> where: :\hat F(i) is the Fock operator for the ''i''-th electron in the system, :(i) is the one-electron Hamiltonian Hamiltonian may refer to: * Hamiltonian mechanics, a function that represents the total energy of a system * Hamiltonian (quantum mechanics), an operator corresponding to the total ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
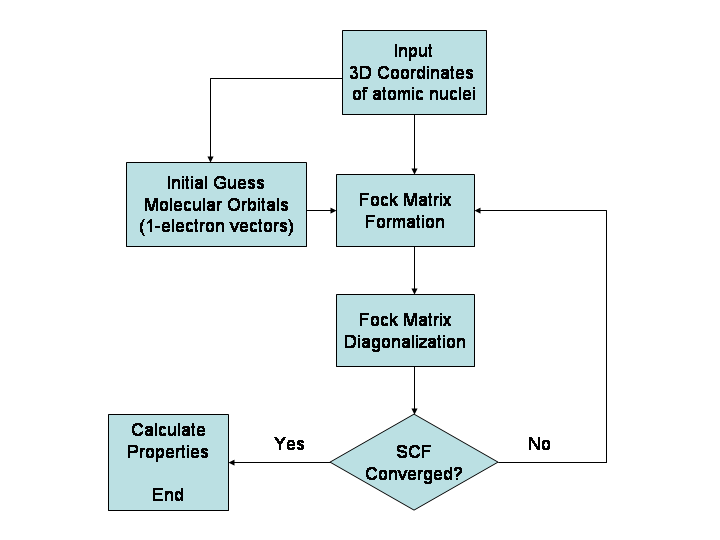
Hartree–Fock Method
In computational physics and chemistry, the Hartree–Fock (HF) method is a method of approximation for the determination of the wave function and the energy of a quantum many-body system in a stationary state. The method is named after Douglas Hartree and Vladimir Fock. The Hartree–Fock method often assumes that the exact ''N''-body wave function of the system can be approximated by a single Slater determinant (in the case where the particles are fermions) or by a single permanent (in the case of bosons) of ''N'' spin-orbitals. By invoking the variational method, one can derive a set of ''N''-coupled equations for the ''N'' spin orbitals. A solution of these equations yields the Hartree–Fock wave function and energy of the system. Hartree–Fock approximation is an instance of mean-field theory, where neglecting higher-order fluctuations in order parameter allows interaction terms to be replaced with quadratic terms, obtaining exactly solvable Hamiltonians. Especially ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Møller–Plesset Perturbation Theory
Møller–Plesset perturbation theory (MP) is one of several quantum chemistry post-Hartree–Fock ab initio methods in the field of computational chemistry. It improves on the Hartree–Fock method by adding electron correlation effects by means of Rayleigh–Schrödinger perturbation theory (RS-PT), usually to second (MP2), third (MP3) or fourth (MP4) order. Its main idea was published as early as 1934 by Christian Møller and Milton S. Plesset. Rayleigh–Schrödinger perturbation theory The MP perturbation theory is a special case of RS perturbation theory. In RS theory one considers an unperturbed Hamiltonian operator \hat_, to which a small (often external) perturbation \hat is added: :\hat = \hat_ + \lambda \hat. Here, ''λ'' is an arbitrary real parameter that controls the size of the perturbation. In MP theory the zeroth-order wave function is an exact eigenfunction of the Fock operator, which thus serves as the unperturbed operator. The perturbation is the c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Slater Determinant
In quantum mechanics, a Slater determinant is an expression that describes the wave function of a multi-fermionic system. It satisfies anti-symmetry requirements, and consequently the Pauli principle, by changing sign upon exchange of two fermions.Molecular Quantum Mechanics Parts I and II: An Introduction to QUANTUM CHEMISTRY (Volume 1), P. W. Atkins, Oxford University Press, 1977, . Only a small subset of all possible many-body fermionic wave functions can be written as a single Slater determinant, but those form an important and useful subset because of their simplicity. The Slater determinant arises from the consideration of a wave function for a collection of electrons, each with a wave function known as the spin-orbital \chi(\mathbf), where \mathbf denotes the position and spin of a single electron. A Slater determinant containing two electrons with the same spin orbital would correspond to a wave function that is zero everywhere. The Slater determinant is named for John ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coulomb Interaction
Coulomb's inverse-square law, or simply Coulomb's law, is an experimental law of physics that calculates the amount of force between two electrically charged particles at rest. This electric force is conventionally called the ''electrostatic force'' or Coulomb force. Although the law was known earlier, it was first published in 1785 by French physicist Charles-Augustin de Coulomb. Coulomb's law was essential to the development of the theory of electromagnetism and maybe even its starting point, as it allowed meaningful discussions of the amount of electric charge in a particle. The law states that the magnitude, or absolute value, of the attractive or repulsive electrostatic force between two point charges is directly proportional to the product of the magnitudes of their charges and inversely proportional to the square of the distance between them. Coulomb discovered that bodies with like electrical charges repel: Coulomb also showed that oppositely charged bodies attract ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Léon Brillouin
Léon Nicolas Brillouin (; August 7, 1889 – October 4, 1969) was a French physicist. He made contributions to quantum mechanics, radio wave propagation in the atmosphere, solid-state physics, and information theory. Early life Brillouin was born in Sèvres, near Paris, France. His father, Marcel Brillouin, grandfather, Éleuthère Mascart, and great-grandfather, Charles Briot, were physicists as well. Education From 1908 to 1912, Brillouin studied physics at the École Normale Supérieure, in Paris. From 1911 he studied under Jean Perrin until he left for the Ludwig Maximilian University of Munich (LMU), in 1912. At LMU, he studied theoretical physics with Arnold Sommerfeld. Just a few months before Brillouin's arrival at LMU, Max von Laue had conducted his experiment showing X-ray diffraction in a crystal lattice. In 1913, he went back to France to study at the University of Paris and it was in this year that Niels Bohr submitted his first paper on the Bohr model of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electronic Hamiltonian
In atomic, molecular, and optical physics and quantum chemistry, the molecular Hamiltonian is the Hamiltonian operator representing the energy of the electrons and nuclei in a molecule. This operator and the associated Schrödinger equation play a central role in computational chemistry and physics for computing properties of molecules and aggregates of molecules, such as thermal conductivity, specific heat, electrical conductivity, optical, and magnetic properties, and reactivity. The elementary parts of a molecule are the nuclei, characterized by their atomic numbers, ''Z'', and the electrons, which have negative elementary charge, −''e''. Their interaction gives a nuclear charge of ''Z'' + ''q'', where , with ''N'' equal to the number of electrons. Electrons and nuclei are, to a very good approximation, point charges and point masses. The molecular Hamiltonian is a sum of several terms: its major terms are the kinetic energies of the electrons and the Coulomb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |