|
Breit Equation
The Breit equation is a relativistic wave equation derived by Gregory Breit in 1929 based on the Dirac equation, which formally describes two or more massive spin-1/2 particles (electrons, for example) interacting electromagnetically to the first order in perturbation theory. It accounts for magnetic interactions and retardation effects to the order of ''1/c2''. When other quantum electrodynamic effects are negligible, this equation has been shown to give results in good agreement with experiment. It was originally derived from the Darwin Lagrangian but later vindicated by the Wheeler–Feynman absorber theory and eventually quantum electrodynamics. Introduction The Breit equation is not only an approximation in terms of quantum mechanics, but also in terms of relativity theory as it is not completely invariant with respect to the Lorentz transformation. Just as does the Dirac equation, it treats nuclei as point sources of an external field for the particles it describes. For ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theory Of Relativity
The theory of relativity usually encompasses two interrelated theories by Albert Einstein: special relativity and general relativity, proposed and published in 1905 and 1915, respectively. Special relativity applies to all physical phenomena in the absence of gravity. General relativity explains the law of gravitation and its relation to the forces of nature. It applies to the cosmological and astrophysical realm, including astronomy. The theory transformed theoretical physics and astronomy during the 20th century, superseding a 200-year-old theory of mechanics created primarily by Isaac Newton. It introduced concepts including 4-dimensional spacetime as a unified entity of space and time, relativity of simultaneity, kinematic and gravitational time dilation, and length contraction. In the field of physics, relativity improved the science of elementary particles and their fundamental interactions, along with ushering in the nuclear age. With relativity, cosmology and astro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
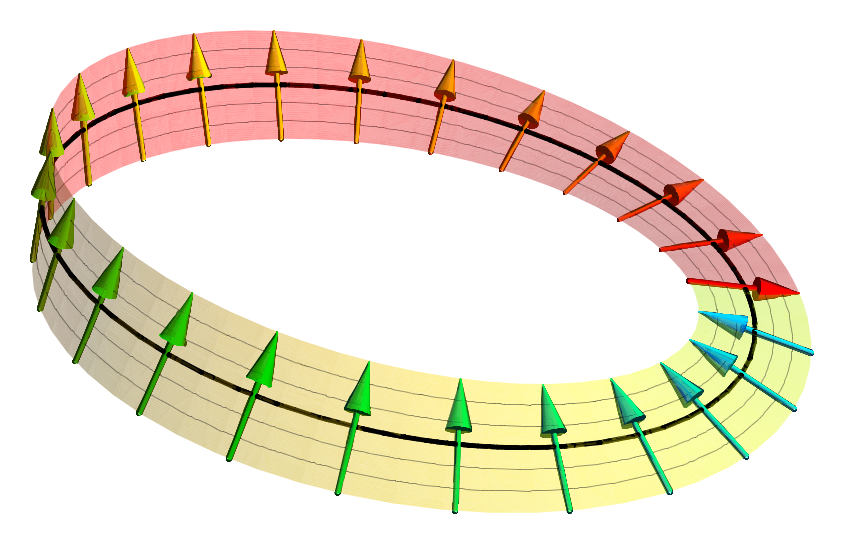
Spinor
In geometry and physics, spinors are elements of a complex vector space that can be associated with Euclidean space. Like geometric vectors and more general tensors, spinors transform linearly when the Euclidean space is subjected to a slight ( infinitesimal) rotation. Unlike vectors and tensors, a spinor transforms to its negative when the space is continuously rotated through a complete turn from 0° to 360° (see picture). This property characterizes spinors: spinors can be viewed as the "square roots" of vectors (although this is inaccurate and may be misleading; they are better viewed as "square roots" of sections of vector bundles – in the case of the exterior algebra bundle of the cotangent bundle, they thus become "square roots" of differential forms). It is also possible to associate a substantially similar notion of spinor to Minkowski space, in which case the Lorentz transformations of special relativity play the role of rotations. Spinors were introduced in ge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positronium
Positronium (Ps) is a system consisting of an electron and its anti-particle, a positron, bound together into an exotic atom, specifically an onium. Unlike hydrogen, the system has no protons. The system is unstable: the two particles annihilate each other to predominantly produce two or three gamma-rays, depending on the relative spin states. The energy levels of the two particles are similar to that of the hydrogen atom (which is a bound state of a proton and an electron). However, because of the reduced mass, the frequencies of the spectral lines are less than half of those for the corresponding hydrogen lines. States The mass of positronium is 1.022 MeV, which is twice the electron mass minus the binding energy of a few eV. The lowest energy orbital state of positronium is 1S, and like with hydrogen, it has a hyperfine structure arising from the relative orientations of the spins of the electron and the positron. The ''singlet'' state, , with antiparallel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Two-body Dirac Equations
In quantum field theory, and in the significant subfields of quantum electrodynamics (QED) and quantum chromodynamics (QCD), the two-body Dirac equations (TBDE) of constraint dynamics provide a three-dimensional yet manifestly covariant reformulation of the Bethe–Salpeter equation for two spin-1/2 particles. Such a reformulation is necessary since without it, as shown by Nakanishi, the Bethe–Salpeter equation possesses negative-norm solutions arising from the presence of an essentially relativistic degree of freedom, the relative time. These "ghost" states have spoiled the naive interpretation of the Bethe–Salpeter equation as a quantum mechanical wave equation. The two-body Dirac equations of constraint dynamics rectify this flaw. The forms of these equations can not only be derived from quantum field theory they can also be derived purely in the context of Dirac's constraint dynamics P.A.M. Dirac, Lectures on Quantum Mechanics (Yeshiva University, New York, 1964) and relativ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bethe–Salpeter Equation
The Bethe–Salpeter equation (named after Hans Bethe and Edwin Salpeter) describes the bound states of a two-body (particles) quantum field theoretical system in a relativistically covariant formalism. The equation was actually first published in 1950 at the end of a paper by Yoichiro Nambu, but without derivation. Due to its generality and its application in many branches of theoretical physics, the Bethe–Salpeter equation appears in many different forms. One form, that is quite often used in high energy physics is : \Gamma(P,p) =\int\!\frac \; K(P,p,k)\, S(k-\tfrac) \,\Gamma(P,k)\, S(k+\tfrac) where ''Γ'' is the Bethe–Salpeter amplitude, ''K'' the interaction and ''S'' the propagators of the two participating particles. In quantum theory, bound states are objects with lifetimes that are much longer than the time-scale of the interaction ruling their structure (otherwise they are called resonances). Thus the constituents interact essentially infinitely many times ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bohr Magneton
In atomic physics, the Bohr magneton (symbol ) is a physical constant and the natural unit for expressing the magnetic moment of an electron caused by its orbital or spin angular momentum. The Bohr magneton, in SI units is defined as \mu_\mathrm = \frac , And in Gaussian CGS units: \mu_\mathrm = \frac , where * is the elementary charge, * is the reduced Planck constant, * is the electron rest mass, * is the speed of light. History The idea of elementary magnets is due to Walther Ritz (1907) and Pierre Weiss. Already before the Rutherford model of atomic structure, several theorists commented that the magneton should involve the Planck constant ''h''. By postulating that the ratio of electron kinetic energy to orbital frequency should be equal to ''h'', Richard Gans computed a value that was twice as large as the Bohr magneton in September 1911. At the First Solvay Conference in November that year, Paul Langevin obtained a e\hbar/(12m_\mathrm). Langevin assumed that the attr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermi Contact Interaction
The Fermi contact interaction is the magnetic interaction between an electron and an atomic nucleus. Its major manifestation is in electron paramagnetic resonance and nuclear magnetic resonance spectroscopies, where it is responsible for the appearance of isotropic hyperfine coupling. This requires that the electron occupy an s-orbital. The interaction is described with the parameter ''A'', which takes the units megahertz. The magnitude of ''A'' is given by this relationships : A = -\frac \pi \left \langle \boldsymbol_n \cdot \boldsymbol_e \right \rangle , \Psi (0), ^2\qquad \mbox and : A = -\frac \mu_0 \left \langle \boldsymbol_n \cdot \boldsymbol_e \right \rangle , \Psi(0), ^2, \qquad \mbox where ''A'' is the energy of the interaction, ''μ''''n'' is the nuclear magnetic moment, ''μ''''e'' is the electron magnetic dipole moment, Ψ(0) is the value of the electron wavefunction at the nucleus, and \left\langle \cdots \right\rangle denotes the quantum mechanical spin coupling. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fine Structure
In atomic physics, the fine structure describes the splitting of the spectral lines of atoms due to electron spin and relativistic corrections to the non-relativistic Schrödinger equation. It was first measured precisely for the hydrogen atom by Albert A. Michelson and Edward W. Morley in 1887, laying the basis for the theoretical treatment by Arnold Sommerfeld, introducing the fine-structure constant. Background Gross structure The ''gross structure'' of line spectra is the line spectra predicted by the quantum mechanics of non-relativistic electrons with no spin. For a hydrogenic atom, the gross structure energy levels only depend on the principal quantum number ''n''. However, a more accurate model takes into account relativistic and spin effects, which break the degeneracy of the energy levels and split the spectral lines. The scale of the fine structure splitting relative to the gross structure energies is on the order of (''Zα'')2, where ''Z'' is the atomic number and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin–orbit Interaction
In quantum physics, the spin–orbit interaction (also called spin–orbit effect or spin–orbit coupling) is a relativistic interaction of a particle's spin with its motion inside a potential. A key example of this phenomenon is the spin–orbit interaction leading to shifts in an electron's atomic energy levels, due to electromagnetic interaction between the electron's magnetic dipole, its orbital motion, and the electrostatic field of the positively charged nucleus. This phenomenon is detectable as a splitting of spectral lines, which can be thought of as a Zeeman effect product of two relativistic effects: the apparent magnetic field seen from the electron perspective and the magnetic moment of the electron associated with its intrinsic spin. A similar effect, due to the relationship between angular momentum and the strong nuclear force, occurs for protons and neutrons moving inside the nucleus, leading to a shift in their energy levels in the nucleus shell model. In the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nuclear Magnetic Resonance
Nuclear magnetic resonance (NMR) is a physical phenomenon in which nuclei in a strong constant magnetic field are perturbed by a weak oscillating magnetic field (in the near field) and respond by producing an electromagnetic signal with a frequency characteristic of the magnetic field at the nucleus. This process occurs near resonance, when the oscillation frequency matches the intrinsic frequency of the nuclei, which depends on the strength of the static magnetic field, the chemical environment, and the magnetic properties of the isotope involved; in practical applications with static magnetic fields up to ca. 20 tesla, the frequency is similar to VHF and UHF television broadcasts (60–1000 MHz). NMR results from specific magnetic properties of certain atomic nuclei. Nuclear magnetic resonance spectroscopy is widely used to determine the structure of organic molecules in solution and study molecular physics and crystals as well as non-crystalline materials. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bispinor
In physics, and specifically in quantum field theory, a bispinor, is a mathematical construction that is used to describe some of the fundamental particles of nature, including quarks and electrons. It is a specific embodiment of a spinor, specifically constructed so that it is consistent with the requirements of special relativity. Bispinors transform in a certain "spinorial" fashion under the action of the Lorentz group, which describes the symmetries of Minkowski spacetime. They occur in the relativistic Spin-1/2, spin- wave function solutions to the Dirac equation. Bispinors are so called because they are constructed out of two simpler component spinors, the Weyl spinors. Each of the two component spinors transform differently under the two distinct complex-conjugate spin-1/2 Representation (mathematics), representations of the Lorentz group. This pairing is of fundamental importance, as it allows the represented particle to have a mass, carry a charge (physics), charge, and r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lorentz Transformation
In physics, the Lorentz transformations are a six-parameter family of linear transformations from a coordinate frame in spacetime to another frame that moves at a constant velocity relative to the former. The respective inverse transformation is then parameterized by the negative of this velocity. The transformations are named after the Dutch physicist Hendrik Lorentz. The most common form of the transformation, parametrized by the real constant v, representing a velocity confined to the -direction, is expressed as \begin t' &= \gamma \left( t - \frac \right) \\ x' &= \gamma \left( x - v t \right)\\ y' &= y \\ z' &= z \end where and are the coordinates of an event in two frames with the origins coinciding at 0, where the primed frame is seen from the unprimed frame as moving with speed along the -axis, where is the speed of light, and \gamma = \left ( \sqrt\right )^ is the Lorentz factor. When speed is much smaller than , the Lorentz factor is negligibly different from ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |