|
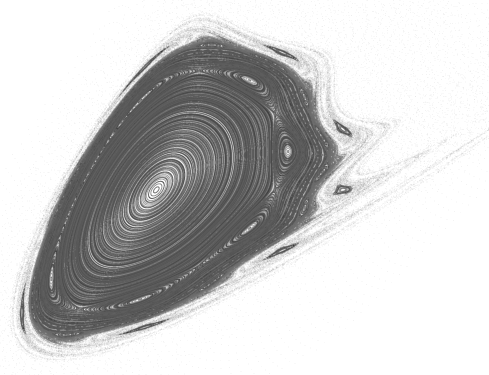
Bogdanov Map
In dynamical systems theory, the Bogdanov map is a chaotic 2D map related to the Bogdanov–Takens bifurcation. It is given by the transformation: : \begin x_ = x_n + y_\\ y_ = y_n + \epsilon y_n + k x_n (x_n - 1) + \mu x_n y_n \end The Bogdanov map is named after Rifkat Bogdanov. See also * List of chaotic maps References * DK Arrowsmith, CM Place, An introduction to dynamical systems, Cambridge University Press, 1990. * Arrowsmith, D. K.; Cartwright, J. H. E.; Lansbury, A. N.; and Place, C. M. "The Bogdanov Map: Bifurcations, Mode Locking, and Chaos in a Dissipative System." Int. J. Bifurcation Chaos 3, 803–842, 1993. * Bogdanov, R. "Bifurcations of a Limit Cycle for a Family of Vector Fields on the Plane." Selecta Math. Soviet 1, 373–388, 1981. External linksBogdanov mapat MathWorld ''MathWorld'' is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partial ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Dynamical Systems Theory
Dynamical systems theory is an area of mathematics used to describe the behavior of complex systems, complex dynamical systems, usually by employing differential equations by nature of the ergodic theory, ergodicity of dynamic systems. When differential equations are employed, the theory is called continuous time, ''continuous dynamical systems''. From a physical point of view, continuous dynamical systems is a generalization of classical mechanics, a generalization where the equations of motion are postulated directly and are not constrained to be Euler–Lagrange equations of a Principle of least action, least action principle. When difference equations are employed, the theory is called discrete time, ''discrete dynamical systems''. When the time variable runs over a set that is discrete over some intervals and continuous over other intervals or is any arbitrary time-set such as a Cantor set, one gets dynamic equations on time scales. Some situations may also be modeled by mixed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Chaos Theory
Chaos theory is an interdisciplinary area of Scientific method, scientific study and branch of mathematics. It focuses on underlying patterns and Deterministic system, deterministic Scientific law, laws of dynamical systems that are highly sensitive to initial conditions. These were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state (meaning there is sensitive dependence on initial conditions). A metaphor for this behavior is that a butterfly flapping its wings in Brazil can cause or prevent a tornado in Texas. Text was copied from this source, which is avai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Map (mathematics)
In mathematics, a map or mapping is a function (mathematics), function in its general sense. These terms may have originated as from the process of making a map, geographical map: ''mapping'' the Earth surface to a sheet of paper. The term ''map'' may be used to distinguish some special types of functions, such as homomorphisms. For example, a linear map is a homomorphism of vector spaces, while the term linear function may have this meaning or it may mean a linear polynomial. In category theory, a map may refer to a morphism. The term ''transformation'' can be used interchangeably, but ''transformation (function), transformation'' often refers to a function from a set to itself. There are also a few less common uses in logic and graph theory. Maps as functions In many branches of mathematics, the term ''map'' is used to mean a Function (mathematics), function, sometimes with a specific property of particular importance to that branch. For instance, a "map" is a "continuous f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Rifkat Bogdanov
Rifkat Ibragimovich Bogdanov (; June 13, 1950 – November 3, 2013) was a Soviet and Russian mathematician known for contributions to nonlinear dynamical systems, bifurcation theory, and differential geometry. He was an ethnic Tatar. In his work on bifurcations of limit cycles and versal deformations of singular points of vector fields (1975–76), he described a bifurcation of co-dimension 2, which has become known in the literature as the Bogdanov–Takens bifurcation. Born in the village of Mamykovo in Tatarstan, Bogdanov had a doctorate under the supervision of Vladimir Arnoldhttps://mathgenealogy.org/id.php?id=79232 in physico-mathematical sciences and was a professor in two Russian research organizations: the Skobeltsyn Institute of Nuclear Physics at Lomonosov Moscow State University and the Department of Higher Mathematics at MATI — the Tsiolkovskii State Technological University. See also * Bogdanov–Takens bifurcation Selected publications * R. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
List Of Chaotic Maps
In mathematics, a chaotic map is a map (mathematics), map (an Discrete-time dynamical system, evolution function) that exhibits some sort of chaotic behavior. Maps may be parameterized by a discrete-time or a continuous-time parameter. Discrete maps usually take the form of iterated functions. Chaotic maps often occur in the study of dynamical systems. Chaotic maps and Iterated function, iterated functions often generate fractals. Some fractals are studied as objects themselves, as set (mathematics), sets rather than in terms of the maps that generate them. This is often because there are several different iterative procedures that generate the same fractal. See also Universality (dynamical systems). List of chaotic maps List of fractals * Cantor set * de Rham curve * Gravity set, or Mitchell-Green gravity set * Julia set - derived from complex quadratic map * Koch snowflake - special case of de Rham curve * Lyapunov fractal * Mandelbrot set - derived from complex quadratic ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Julyan Cartwright
Julyan Cartwright is an interdisciplinary physicist working in Granada, Spain at the Andalusian Earth Sciences Institute of the CSIC (Spanish National Research Council) and affiliated with the Carlos I Institute of Theoretical and Computational Physics at the University of Granada. He is known for his research on how form and pattern emerge in nature, the dynamics of natural systems, across disciplinary boundaries, including his studies of the dynamics of passive scalars in chaotic advection of fluids, bailout embeddings, the Bogdanov map, the influence of fluid mechanics on the development of vertebrate left-right asymmetry, self-organization of biomineralization structures of mollusc shell including mother of pearl (nacre) and cuttlebone, excitable media, and chemobrionics: self-assembling porous precipitate structures, such as chemical gardens, brinicles, and submarine hydrothermal vents. He is among the researchers in the Stanford list of the World's top 2% most cited ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
MathWorld
''MathWorld'' is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at Urbana–Champaign. History Eric W. Weisstein, the creator of the site, was a physics and astronomy student who got into the habit of writing notes on his mathematical readings. In 1995 he put his notes online and called it "Eric's Treasure Trove of Mathematics." It contained hundreds of pages/articles, covering a wide range of mathematical topics. The site became popular as an extensive single resource on mathematics on the web. In 1998, he made a contract with CRC Press and the contents of the site were published in print and CD-ROM form, titled ''CRC Concise Encyclopedia of Mathematics''. The free online version became only partially accessible to the public. In 1999 Weisstein we ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Chaotic Maps
Chaotic was originally a Danish trading card game. It expanded to an online game in America which then became a television program based on the game. The program aired on 4Kids TV (Fox affiliates, nationwide), Jetix, The CW4Kids, Cartoon Network and Disney XD. It was brought over to the United States from Denmark by Bryan C. Gannon and Chaotic USA Entertainment Group, and produced by Chaotic USA Entertainment Group, 4Kids Productions and Bardel Entertainment. The trading card game came out 6 September 2006 in the U.S. and Canada. Each card comes with a unique code which the owner can upload onto the Chaotic website. This allows the owner to trade and play online using their own card collection. The game was well known to be the only game with a TV show, an online game, and a TCG that were all integrated. However, the online game is currently closed. The rights have since defaulted to Bryan C. Gannon, who's leading an effort to revive the game for modern audiences by licensing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Exactly Solvable Models
Exact may refer to: * Exaction, a concept in real property law * ''Ex'Act'', 2016 studio album by Exo * Schooner Exact, the ship which carried the founders of Seattle Companies * Exact (company), a Dutch software company * Exact Change, an American independent book publishing company * Exact Editions, a content management platform Mathematics * Exact differentials, in multivariate calculus * Exact algorithms, in computer science and operations research * Exact colorings, in graph theory * Exact couples, a general source of spectral sequences * Exact sequences, in homological algebra * Exact functor, a function which preserves exact sequences See also * *Exactor (other) *XACT (other) *EXACTO, a sniper rifle {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |