|
Bivariate Von Mises Distribution
In probability theory and statistics, the bivariate von Mises distribution is a probability distribution describing values on a torus. It may be thought of as an analogue on the torus of the bivariate normal distribution. The distribution belongs to the field of directional statistics. The general bivariate von Mises distribution was first proposed by Kanti Mardia in 1975. One of its variants is today used in the field of bioinformatics to formulate a probabilistic model of protein structure in atomic detail, such as backbone-dependent rotamer libraries. Definition The bivariate von Mises distribution is a probability distribution defined on the torus, S^1 \times S^1 in \mathbb^3. The probability density function of the general bivariate von Mises distribution for the angles \phi, \psi \in , 2\pi/math> is given by : f(\phi, \psi) \propto \exp \kappa_1 \cos(\phi - \mu) + \kappa_2 \cos(\psi - \nu) + (\cos(\phi-\mu), \sin(\phi-\mu)) \mathbf (\cos(\psi - \nu), \sin(\psi - ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bivariate Von Mises Distribution Cosine Samples
{{disambiguation ...
Bivariate may refer to: Mathematics * Bivariate function, a function of two variables * Bivariate polynomial, a polynomial of two indeterminates Statistics * Bivariate data, that shows the relationship between two variables * Bivariate analysis, statistical analysis of two variables * Bivariate distribution, a joint probability distribution for two variables Other * Bivariate map, a single map that displays two variables See also * Two-dimensional curve * Multivariate (other) Multivariate may refer to: In mathematics * Multivariable calculus * Multivariate function * Multivariate polynomial In computing * Multivariate cryptography * Multivariate division algorithm * Multivariate interpolation * Multivariate optical c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Theory
Probability theory is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms of probability, axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure (mathematics), measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event (probability theory), event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of determinism, non-deterministic or uncertain processes or measured Quantity, quantities that may either be single occurrences or evolve over time in a random fashion). Although it is not possible to perfectly p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Distribution
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon in terms of its sample space and the probabilities of events (subsets of the sample space). For instance, if is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of would take the value 0.5 (1 in 2 or 1/2) for , and 0.5 for (assuming that the coin is fair). Examples of random phenomena include the weather conditions at some future date, the height of a randomly selected person, the fraction of male students in a school, the results of a survey to be conducted, etc. Introduction A probability distribution is a mathematical description of the probabilities of events, subsets of the sample space. The sample space, often denoted by \Omega, is the set of all possible outcomes of a ra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torus
In geometry, a torus (plural tori, colloquially donut or doughnut) is a surface of revolution generated by revolving a circle in three-dimensional space about an axis that is coplanar with the circle. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a spindle torus. If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a '' toroid'', as in a square toroid. Real-world objects that approximate a torus of revolution include swim rings, inner tubes and ringette rings. Eyeglass lenses that combine spherical and cylindrical correction are toric lenses. A torus should not be confused with a ''solid torus'', which is form ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multivariate Normal Distribution
In probability theory and statistics, the multivariate normal distribution, multivariate Gaussian distribution, or joint normal distribution is a generalization of the one-dimensional ( univariate) normal distribution to higher dimensions. One definition is that a random vector is said to be ''k''-variate normally distributed if every linear combination of its ''k'' components has a univariate normal distribution. Its importance derives mainly from the multivariate central limit theorem. The multivariate normal distribution is often used to describe, at least approximately, any set of (possibly) correlated real-valued random variables each of which clusters around a mean value. Definitions Notation and parameterization The multivariate normal distribution of a ''k''-dimensional random vector \mathbf = (X_1,\ldots,X_k)^ can be written in the following notation: : \mathbf\ \sim\ \mathcal(\boldsymbol\mu,\, \boldsymbol\Sigma), or to make it explicitly known that ''X ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Directional Statistics
Directional statistics (also circular statistics or spherical statistics) is the subdiscipline of statistics that deals with directions (unit vectors in Euclidean space, R''n''), axes ( lines through the origin in R''n'') or rotations in R''n''. More generally, directional statistics deals with observations on compact Riemannian manifolds including the Stiefel manifold. The fact that 0 degrees and 360 degrees are identical angles, so that for example 180 degrees is not a sensible mean of 2 degrees and 358 degrees, provides one illustration that special statistical methods are required for the analysis of some types of data (in this case, angular data). Other examples of data that may be regarded as directional include statistics involving temporal periods (e.g. time of day, week, month, year, etc.), compass directions, dihedral angles in molecules, orientations, rotations and so on. Circular distributions Any probability density function (pdf) \ p(x) on the line can be "wra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kanti Mardia
Kantilal Vardichand "Kanti" Mardia (born 1935) is an Indian-British statistician specialising in directional statistics, multivariate analysis, geostatistics, statistical bioinformatics and statistical shape analysis. He was born in Sirohi, Rajasthan, India in a Jain family and now resides and works in Leeds. He is known for his series of tests of multivariate normality based measures of multivariate skewness and kurtosis as well as work on the statistical measures of shape. Life and career Mardia was educated at the Ismail Yusuf College at the University of Bombay (BSc 1955, MSc in statistics 1957), the University of Poona (MSc in pure mathematics 1961), the University of Rajasthan (PhD 1965) and the University of Newcastle Upon Tyne (PhD 1967, DSc 1973). He held academic positions at the Institute of Science, Mumbai and the University of Hull. Mardia was appointed professor of applied statistics and head of the Department of Statistics in the School of Mathematics at the Un ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bioinformatics
Bioinformatics () is an interdisciplinary field that develops methods and software tools for understanding biological data, in particular when the data sets are large and complex. As an interdisciplinary field of science, bioinformatics combines biology, chemistry, physics, computer science, information engineering, mathematics and statistics to analyze and interpret the biological data. Bioinformatics has been used for '' in silico'' analyses of biological queries using computational and statistical techniques. Bioinformatics includes biological studies that use computer programming as part of their methodology, as well as specific analysis "pipelines" that are repeatedly used, particularly in the field of genomics. Common uses of bioinformatics include the identification of candidates genes and single nucleotide polymorphisms ( SNPs). Often, such identification is made with the aim to better understand the genetic basis of disease, unique adaptations, desirable propertie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
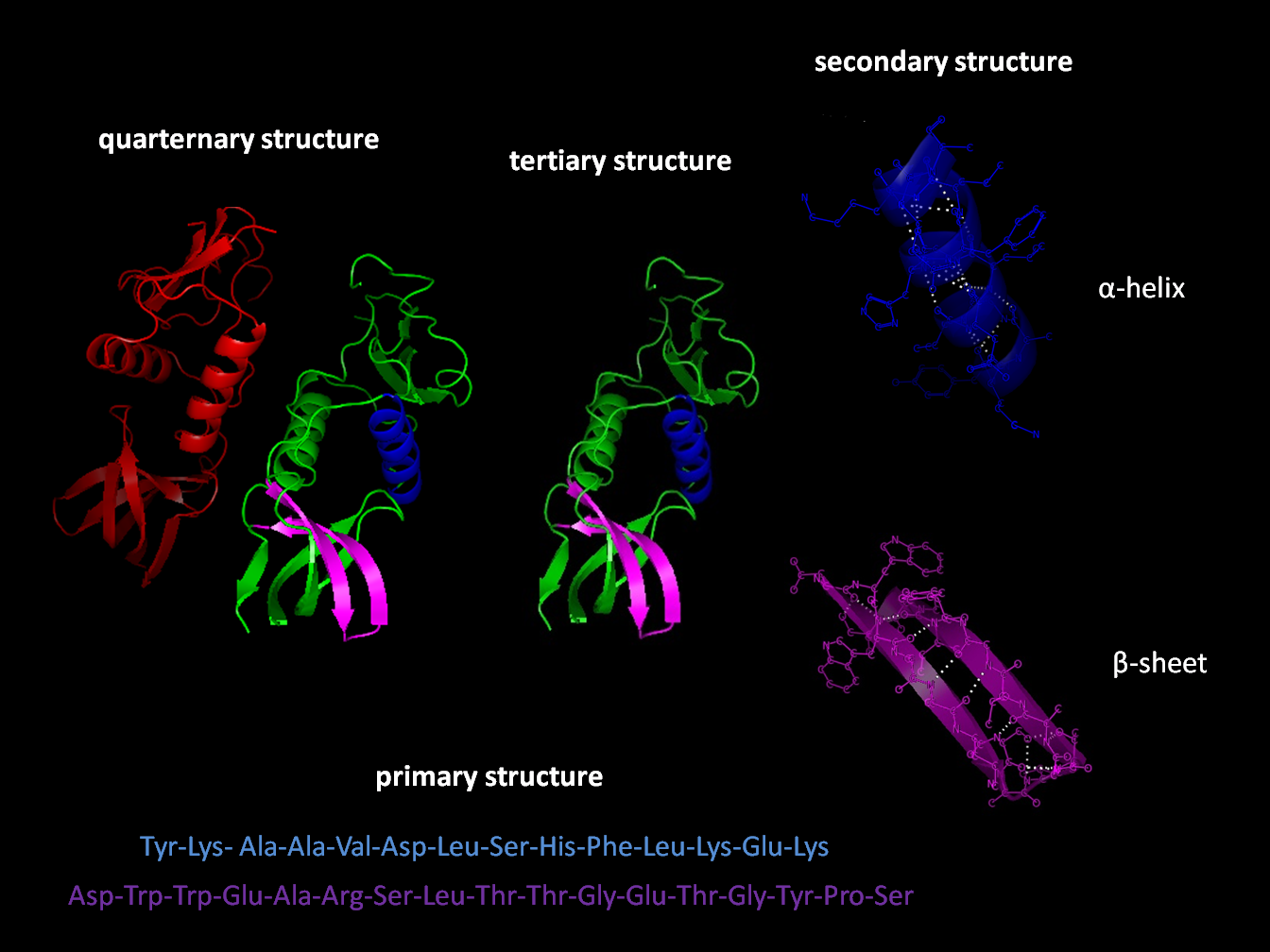
Protein Structure
Protein structure is the molecular geometry, three-dimensional arrangement of atoms in an amino acid-chain molecule. Proteins are polymers specifically polypeptides formed from sequences of amino acids, the monomers of the polymer. A single amino acid monomer may also be called a ''residue'' indicating a repeating unit of a polymer. Proteins form by amino acids undergoing condensation reactions, in which the amino acids lose one water molecule per chemical reaction, reaction in order to attach to one another with a peptide bond. By convention, a chain under 30 amino acids is often identified as a peptide, rather than a protein. To be able to perform their biological function, proteins fold into one or more specific spatial conformations driven by a number of non-covalent interactions such as hydrogen bonding, ionic interactions, Van der Waals forces, and hydrophobic packing. To understand the functions of proteins at a molecular level, it is often necessary to determine their Pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Backbone-dependent Rotamer Library
In biochemistry, a backbone-dependent rotamer library provides the frequencies, mean dihedral angles, and standard deviations of the discrete conformations (known as rotamers) of the amino acid side chains in proteins as a function of the backbone dihedral angles φ and ψ of the Ramachandran map. By contrast, backbone-independent rotamer libraries express the frequencies and mean dihedral angles for all side chains in proteins, regardless of the backbone conformation of each residue type. Backbone-dependent rotamer libraries have been shown to have significant advantages over backbone-independent rotamer libraries, principally when used as an energy term, by speeding up search times of side-chain packing algorithms used in protein structure prediction and protein design. History The first backbone-dependent rotamer library was developed in 1993 by Roland Dunbrack and Martin Karplus to assist the prediction of the Cartesian coordinates of a protein's side chains given the expe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Von Mises Distribution
In probability theory and directional statistics, the von Mises distribution (also known as the circular normal distribution or Tikhonov distribution) is a continuous probability distribution on the circle. It is a close approximation to the wrapped normal distribution, which is the circular analogue of the normal distribution. A freely diffusing angle \theta on a circle is a wrapped normally distributed random variable with an unwrapped variance that grows linearly in time. On the other hand, the von Mises distribution is the stationary distribution of a drift and diffusion process on the circle in a harmonic potential, i.e. with a preferred orientation. The von Mises distribution is the maximum entropy distribution for circular data when the real and imaginary parts of the first circular moment are specified. The von Mises distribution is a special case of the von Mises–Fisher distribution on the ''N''-dimensional sphere. Definition The von Mises probability density fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |