|
Bayesian Statistic
Bayesian statistics is a theory in the field of statistics based on the Bayesian probability, Bayesian interpretation of probability where probability expresses a ''degree of belief'' in an Event (probability theory), event. The degree of belief may be based on prior knowledge about the event, such as the results of previous experiments, or on personal beliefs about the event. This differs from a number of other Probability interpretations, interpretations of probability, such as the Frequentist probability, frequentist interpretation that views probability as the Limit of a sequence, limit of the relative frequency of an event after many trials. Bayesian statistical methods use Bayes' theorem to compute and update probabilities after obtaining new data. Bayes' theorem describes the conditional probability of an event based on data as well as prior information or beliefs about the event or conditions related to the event. For example, in Bayesian inference, Bayes' theorem can be u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bayesian Inference
Bayesian inference is a method of statistical inference in which Bayes' theorem is used to update the probability for a hypothesis as more evidence or information becomes available. Bayesian inference is an important technique in statistics, and especially in mathematical statistics. Bayesian updating is particularly important in the dynamic analysis of a sequence of data. Bayesian inference has found application in a wide range of activities, including science, engineering, philosophy, medicine, sport, and law. In the philosophy of decision theory, Bayesian inference is closely related to subjective probability, often called "Bayesian probability". Introduction to Bayes' rule Formal explanation Bayesian inference derives the posterior probability as a consequence of two antecedents: a prior probability and a "likelihood function" derived from a statistical model for the observed data. Bayesian inference computes the posterior probability according to Bayes' theorem: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ''wikt:Statistik#German, Statistik'', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Theory
Probability theory is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of non-deterministic or uncertain processes or measured quantities that may either be single occurrences or evolve over time in a random fashion). Although it is not possible to perfectly predict random events, much can be said about their behavior. Two major results in probability ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variational Bayesian Methods
Variational Bayesian methods are a family of techniques for approximating intractable integrals arising in Bayesian inference and machine learning. They are typically used in complex statistical models consisting of observed variables (usually termed "data") as well as unknown parameters and latent variables, with various sorts of relationships among the three types of random variables, as might be described by a graphical model. As typical in Bayesian inference, the parameters and latent variables are grouped together as "unobserved variables". Variational Bayesian methods are primarily used for two purposes: #To provide an analytical approximation to the posterior probability of the unobserved variables, in order to do statistical inference over these variables. #To derive a lower bound for the marginal likelihood (sometimes called the ''evidence'') of the observed data (i.e. the marginal probability of the data given the model, with marginalization performed over unobserved v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems of sorts arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries. In the more general approach, an optimization problem consists of maxima and minima, maximizing or minimizing a Function of a real variable, real function by systematically choosing Argument of a function, input values from within an allowed set and computing the Value (mathematics), value of the function. The generalization of optimization theory and techniques to other formulations constitutes a large area of applied mathematics. More generally, opti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mode (statistics)
The mode is the value that appears most often in a set of data values. If is a discrete random variable, the mode is the value (i.e, ) at which the probability mass function takes its maximum value. In other words, it is the value that is most likely to be sampled. Like the statistical mean and median, the mode is a way of expressing, in a (usually) single number, important information about a random variable or a population. The numerical value of the mode is the same as that of the mean and median in a normal distribution, and it may be very different in highly skewed distributions. The mode is not necessarily unique to a given discrete distribution, since the probability mass function may take the same maximum value at several points , , etc. The most extreme case occurs in uniform distributions, where all values occur equally frequently. When the probability density function of a continuous distribution has multiple local maxima it is common to refer to all of the local ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maximum A Posteriori
In Bayesian statistics, a maximum a posteriori probability (MAP) estimate is an estimate of an unknown quantity, that equals the mode of the posterior distribution. The MAP can be used to obtain a point estimate of an unobserved quantity on the basis of empirical data. It is closely related to the method of maximum likelihood (ML) estimation, but employs an augmented optimization objective which incorporates a prior distribution (that quantifies the additional information available through prior knowledge of a related event) over the quantity one wants to estimate. MAP estimation can therefore be seen as a regularization of maximum likelihood estimation. Description Assume that we want to estimate an unobserved population parameter \theta on the basis of observations x. Let f be the sampling distribution of x, so that f(x\mid\theta) is the probability of x when the underlying population parameter is \theta. Then the function: :\theta \mapsto f(x \mid \theta) \! is known as th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral
In mathematics Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ..., an integral assigns numbers to functions in a way that describes Displacement (geometry), displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along with Derivative, differentiation, integration is a fundamental, essential operation of calculus,Integral calculus is a very well established mathematical discipline for which there are many sources. See and , for example. and serves as a tool to solve problems in mathematics and physics involving the area of an arbitrary shape, the length of a curve, and the volume of a solid, among others. The integrals enumerated here are those termed definite integrals, which can be int ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Outcome (probability)
In probability theory, an outcome is a possible result of an experiment or trial. Each possible outcome of a particular experiment is unique, and different outcomes are mutually exclusive (only one outcome will occur on each trial of the experiment). All of the possible outcomes of an experiment form the elements of a sample space. For the experiment where we flip a coin twice, the four possible ''outcomes'' that make up our ''sample space'' are (H, T), (T, H), (T, T) and (H, H), where "H" represents a "heads", and "T" represents a "tails". Outcomes should not be confused with ''events'', which are (or informally, "groups") of outcomes. For comparison, we could define an event to occur when "at least one 'heads'" is flipped in the experiment - that is, when the outcome contains at least one 'heads'. This event would contain all outcomes in the sample space except the element (T, T). Sets of outcomes: events Since individual outcomes may be of little practical interest, or becaus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sample Space
In probability theory, the sample space (also called sample description space, possibility space, or outcome space) of an experiment or random trial is the set of all possible outcomes or results of that experiment. A sample space is usually denoted using set notation, and the possible ordered outcomes, or sample points, are listed as elements in the set. It is common to refer to a sample space by the labels ''S'', Ω, or ''U'' (for "universal set"). The elements of a sample space may be numbers, words, letters, or symbols. They can also be finite, countably infinite, or uncountably infinite. A subset of the sample space is an event, denoted by E. If the outcome of an experiment is included in E, then event E has occurred. For example, if the experiment is tossing a single coin, the sample space is the set \, where the outcome H means that the coin is heads and the outcome T means that the coin is tails. The possible events are E=\, E = \, and E = \. For tossing two coins, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partition Of A Set
In mathematics, a partition of a set is a grouping of its elements into non-empty subsets, in such a way that every element is included in exactly one subset. Every equivalence relation on a set defines a partition of this set, and every partition defines an equivalence relation. A set equipped with an equivalence relation or a partition is sometimes called a setoid, typically in type theory and proof theory. Definition and Notation A partition of a set ''X'' is a set of non-empty subsets of ''X'' such that every element ''x'' in ''X'' is in exactly one of these subsets (i.e., ''X'' is a disjoint union of the subsets). Equivalently, a family of sets ''P'' is a partition of ''X'' if and only if all of the following conditions hold: *The family ''P'' does not contain the empty set (that is \emptyset \notin P). *The union of the sets in ''P'' is equal to ''X'' (that is \textstyle\bigcup_ A = X). The sets in ''P'' are said to exhaust or cover ''X''. See also collectively exhaus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
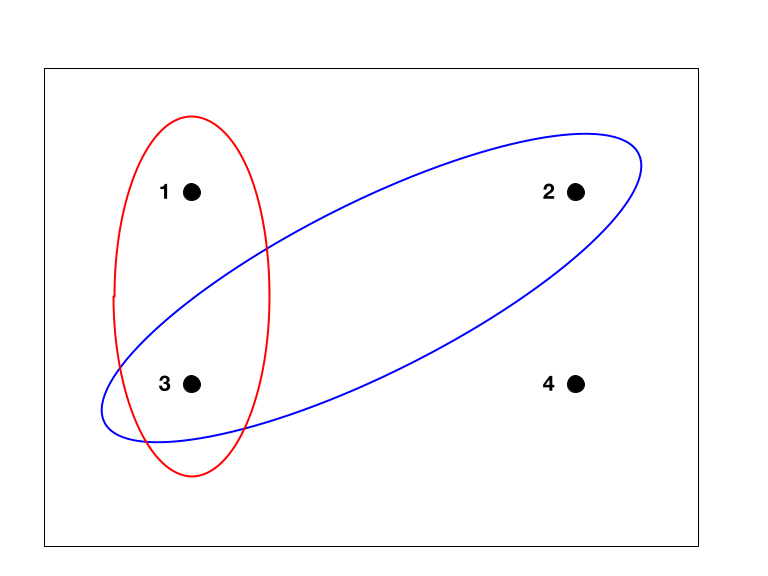
Law Of Total Probability
In probability theory, the law (or formula) of total probability is a fundamental rule relating marginal probabilities to conditional probabilities. It expresses the total probability of an outcome which can be realized via several distinct events, hence the name. Statement The law of total probability isZwillinger, D., Kokoska, S. (2000) ''CRC Standard Probability and Statistics Tables and Formulae'', CRC Press. page 31. a theorem that states, in its discrete case, if \left\ is a finite or countably infinite partition of a sample space (in other words, a set of pairwise disjoint events whose union is the entire sample space) and each event B_n is measurable, then for any event A of the same probability space: :P(A)=\sum_n P(A\cap B_n) or, alternatively, :P(A)=\sum_n P(A\mid B_n)P(B_n), where, for any n for which P(B_n) = 0 these terms are simply omitted from the summation, because P(A\mid B_n) is finite. The summation can be interpreted as a weighted average, and consequ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.svg "Click for more on -> Probability Theory")
