|
Argument Form
In logic, logical form of a statement is a precisely-specified semantic version of that statement in a formal system. Informally, the logical form attempts to formalize a possibly ambiguous statement into a statement with a precise, unambiguous logical interpretation with respect to a formal system. In an ideal formal language, the meaning of a logical form can be determined unambiguously from syntax alone. Logical forms are semantic, not syntactic constructs; therefore, there may be more than one string that represents the same logical form in a given language. The logical form of an argument is called the argument form of the argument. History The importance of the concept of form to logic was already recognized in ancient times. Aristotle, in the ''Prior Analytics'', was probably the first to employ variable letters to represent valid inferences. Therefore, Jan Łukasiewicz claims that the introduction of variables was "one of Aristotle's greatest inventions." According ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modus Ponens Logical Form
Modus may refer to: * Modus, the Latin name for grammatical mood, in linguistics * Modus, the Latin name for mode (statistics) * Modus (company), an Alberta-based company * Modus (medieval music), a term used in several different technical meanings in medieval music theory * The Renault Modus, a small car * Modus (band), a pop music band in former Czechoslovakia ** Modus (album), ''Modus'' (album), 1979, or the title track * Short for ''modus decimandi'', a type of payment made in lieu of a tithe * Modus FX, a visual effects company based in Sainte-Thérèse, Quebec, Canada * Modus (TV series), ''Modus'' (TV series), a Swedish television series, 2015 * "Modus", a song by Joji from his 2020 album ''Nectar (Joji album), Nectar'' See also * ''Modus operandi'' * Modus operandi (other) * ''Modus vivendi'' {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Validity (logic)
In logic, specifically in deductive reasoning, an argument is valid if and only if it takes a form that makes it impossible for the premises to be true and the conclusion nevertheless to be false. It is not required for a valid argument to have premises that are actually true, but to have premises that, if they were true, would guarantee the truth of the argument's conclusion. Valid arguments must be clearly expressed by means of sentences called well-formed formulas (also called ''wffs'' or simply ''formulas''). The validity of an argument can be tested, proved or disproved, and depends on its logical form. Arguments In logic, an argument is a set of statements expressing the ''premises'' (whatever consists of empirical evidences and axiomatic truths) and an ''evidence-based conclusion.'' An argument is ''valid'' if and only if it would be contradictory for the conclusion to be false if all of the premises are true. Validity doesn't require the truth of the premises, inst ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
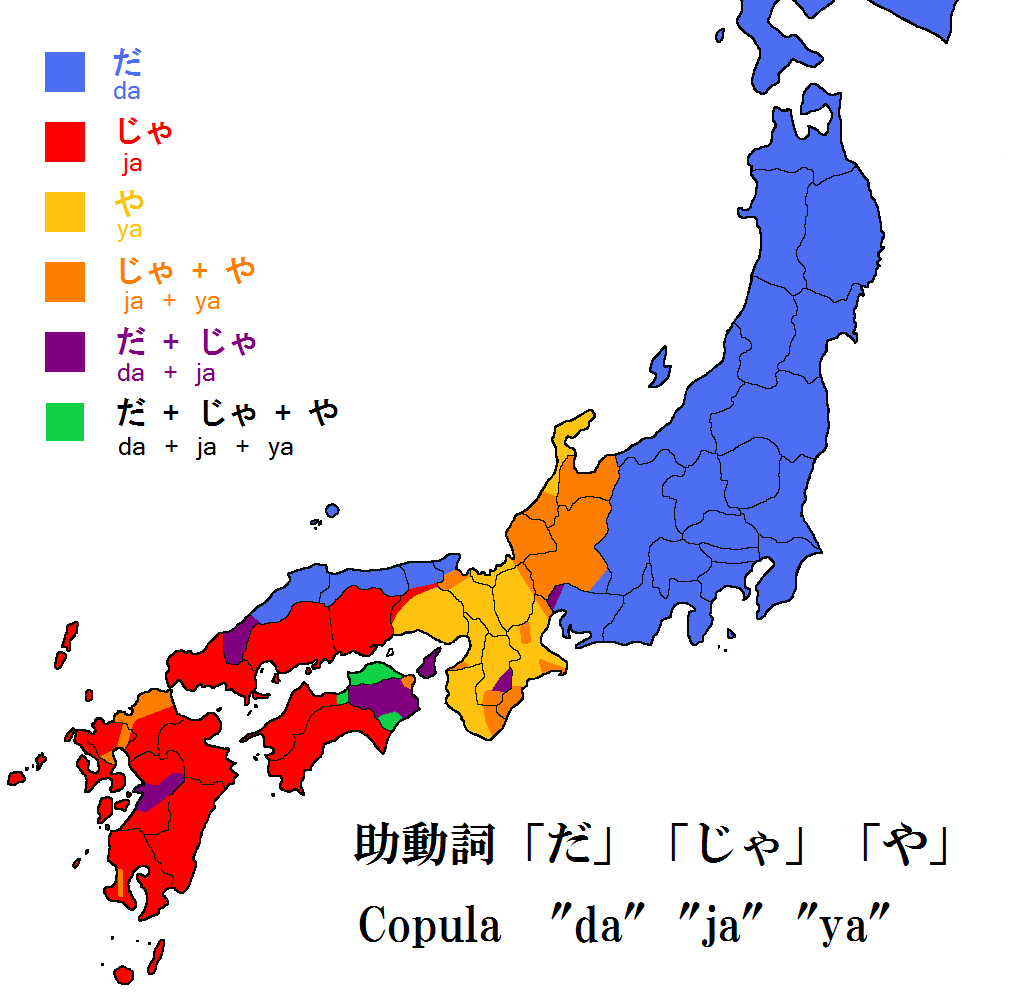
Copula (linguistics)
In linguistics, a copula (plural: copulas or copulae; abbreviated ) is a word or phrase that links the subject of a sentence to a subject complement, such as the word ''is'' in the sentence "The sky is blue" or the phrase ''was not being'' in the sentence "It was not being co-operative." The word ''copula'' derives from the Latin noun for a "link" or "tie" that connects two different things. A copula is often a verb or a verb-like word, though this is not universally the case. A verb that is a copula is sometimes called a copulative or copular verb. In English primary education grammar courses, a copula is often called a linking verb. In other languages, copulas show more resemblances to pronouns, as in Classical Chinese and Guarani, or may take the form of suffixes attached to a noun, as in Korean, Beja, and Inuit languages. Most languages have one main copula, although some (like Spanish, Portuguese and Thai) have more than one, while others have none. In the case of Eng ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schematic Variable
In logic, a metavariable (also metalinguistic variable or syntactical variable) is a symbol or symbol string which belongs to a metalanguage and stands for elements of some object language. For instance, in the sentence :''Let A and B be two sentences of a language ℒ'' the symbols A and B are part of the metalanguage in which the statement about the object language ℒ is formulated. John Corcoran considers this terminology unfortunate because it obscures the use of schemata and because such "variables" do not actually range over a domain. The convention is that a metavariable is to be uniformly substituted with the same instance in all its appearances in a given schema. This is in contrast with nonterminal symbols in formal grammars where the nonterminals on the right of a production can be substituted by different instances.. Attempts to formalize the notion of metavariable result in some kind of type theory.Masahiko Sato, Takafumi Sakurai, Yukiyoshi Kameyama, and Atsushi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Informal Logic
Informal logic encompasses the principles of logic and logical thought outside of a formal setting (characterized by the usage of particular statements). However, the precise definition of "informal logic" is a matter of some dispute. Ralph H. Johnson and J. Anthony Blair define informal logic as "a branch of logic whose task is to develop non-formal standards, criteria, procedures for the analysis, interpretation, evaluation, criticism and construction of argumentation."Johnson, Ralph H., and Blair, J. Anthony (1987), "The Current State of Informal Logic", ''Informal Logic'', 9(2–3), 147–151. Johnson & Blair added "... in everyday discourse" but in (2000), modified their definition, and broadened the focus now to include the sorts of argument that occurs not just in everyday discourse but also disciplined inquiry—what Weinstein (1990) calls "stylized discourse." This definition reflects what had been implicit in their practice and what others were doing in their informal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Argumentation Theory
Argumentation theory, or argumentation, is the interdisciplinary study of how conclusions can be supported or undermined by premises through logical reasoning. With historical origins in logic, dialectic, and rhetoric, argumentation theory, includes the arts and sciences of civil debate, dialogue, conversation, and persuasion. It studies rules of inference, logic, and procedural rules in both artificial and real-world settings. Argumentation includes various forms of dialogue such as deliberation and negotiation which are concerned with collaborative decision-making procedures. It also encompasses eristic dialog, the branch of social debate in which victory over an opponent is the primary goal, and didactic dialogue used for teaching. This discipline also studies the means by which people can express and rationally resolve or at least manage their disagreements. Argumentation is a daily occurrence, such as in public debate, science, and law. For example in law, in courts by the ju ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schema (logic)
In logic, logical form of a statement is a precisely-specified semantic version of that statement in a formal system. Informally, the logical form attempts to formalize a possibly ambiguous statement into a statement with a precise, unambiguous logical interpretation with respect to a formal system. In an ideal formal language, the meaning of a logical form can be determined unambiguously from syntax alone. Logical forms are semantic, not syntactic constructs; therefore, there may be more than one string that represents the same logical form in a given language. The logical form of an argument is called the argument form of the argument. History The importance of the concept of form to logic was already recognized in ancient times. Aristotle, in the '' Prior Analytics'', was probably the first to employ variable letters to represent valid inferences. Therefore, Jan Łukasiewicz claims that the introduction of variables was "one of Aristotle's greatest inventions." According ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compositionality
In semantics, mathematical logic and related disciplines, the principle of compositionality is the principle that the meaning of a complex expression is determined by the meanings of its constituent expressions and the rules used to combine them. This principle is also called Frege's principle, because Gottlob Frege is widely credited for the first modern formulation of it. The principle was never explicitly stated by Frege, and it was arguably already assumed by George Boole decades before Frege's work. The principle of compositionality is highly debated in linguistics, and among its most challenging problems there are the issues of contextuality, the non-compositionality of idiomatic expressions, and the non-compositionality of quotations. History Discussion of compositionality started to appear at the beginning of the 19th century, during which it was debated whether what was most fundamental in language was compositionality or contextuality, and compositionality was usuall ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ordered Set
In mathematics, especially order theory, a partially ordered set (also poset) formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation indicating that, for certain pairs of elements in the set, one of the elements precedes the other in the ordering. The relation itself is called a "partial order." The word ''partial'' in the names "partial order" and "partially ordered set" is used as an indication that not every pair of elements needs to be comparable. That is, there may be pairs of elements for which neither element precedes the other in the poset. Partial orders thus generalize total orders, in which every pair is comparable. Informal definition A partial order defines a notion of comparison. Two elements ''x'' and ''y'' may stand in any of four mutually exclusive relationships to each other: either ''x'' ''y'', or ''x'' and ''y'' are ''incompar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Denying The Antecedent
Denying the antecedent, sometimes also called inverse error or fallacy of the inverse, is a formal fallacy of inferring the inverse from the original statement. It is committed by reasoning in the form: :If ''P'', then ''Q''. :Therefore, if not ''P'', then not ''Q''. which may also be phrased as :P \rightarrow Q (P implies Q) :\therefore \neg P \rightarrow \neg Q (therefore, not-P implies not-Q) Arguments of this form are invalid. Informally, this means that arguments of this form do not give good reason to establish their conclusions, even if their premises are true. In this example, a valid conclusion would be: ~P or Q. The name ''denying the antecedent'' derives from the premise "not ''P''", which denies the "if" clause of the conditional premise. One way to demonstrate the invalidity of this argument form is with an example that has true premises but an obviously false conclusion. For example: :If you are a ski instructor, then you have a job. :You are not a ski ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Affirming The Consequent
Affirming the consequent, sometimes called converse error, fallacy of the converse, or confusion of necessity and sufficiency, is a formal fallacy of taking a true conditional statement (e.g., "If the lamp were broken, then the room would be dark"), and invalidly inferring its converse ("The room is dark, so the lamp is broken"), even though that statement may not be true. This arises when a consequent ("the room would be dark") has other possible antecedents (for example, "the lamp is in working order, but is switched off" or "there is no lamp in the room"). Converse errors are common in everyday thinking and communication and can result from, among other causes, communication issues, misconceptions about logic, and failure to consider other causes. The opposite statement, denying the consequent, ''is'' a valid form of argument (modus tollens). Formal description Affirming the consequent is the action of taking a true statement P \to Q and invalidly concluding its converse Q \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modus Tollens
In propositional logic, ''modus tollens'' () (MT), also known as ''modus tollendo tollens'' (Latin for "method of removing by taking away") and denying the consequent, is a deductive argument form and a rule of inference. ''Modus tollens'' takes the form of "If P, then Q. Not Q. Therefore, not P." It is an application of the general truth that if a statement is true, then so is its contrapositive. The form shows that inference from ''P implies Q'' to ''the negation of Q implies the negation of P'' is a valid argument. The history of the inference rule ''modus tollens'' goes back to antiquity. The first to explicitly describe the argument form ''modus tollens'' was Theophrastus. ''Modus tollens'' is closely related to '' modus ponens''. There are two similar, but invalid, forms of argument: affirming the consequent and denying the antecedent. See also contraposition and proof by contrapositive. Explanation The form of a ''modus tollens'' argument resembles a syllog ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |