|
Alternative Hypothesis
In statistical hypothesis testing, the alternative hypothesis is one of the proposed proposition in the hypothesis test. In general the goal of hypothesis test is to demonstrate that in the given condition, there is sufficient evidence supporting the credibility of alternative hypothesis instead of the exclusive proposition in the test (null hypothesis). It is usually consistent with the research hypothesis because it is constructed from literature review, previous studies, etc. However, the research hypothesis is sometimes consistent with the null hypothesis. In statistics, alternative hypothesis is often denoted as Ha or H1. Hypotheses are formulated to compare in a statistical hypothesis test. In the domain of inferential statistics two rival hypotheses can be compared by explanatory power and predictive power. Basic definition The ''alternative hypothesis'' and ''null hypothesis'' are types of conjectures used in statistical tests, which are formal methods of reaching ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Hypothesis Testing
A statistical hypothesis test is a method of statistical inference used to decide whether the data at hand sufficiently support a particular hypothesis. Hypothesis testing allows us to make probabilistic statements about population parameters. History Early use While hypothesis testing was popularized early in the 20th century, early forms were used in the 1700s. The first use is credited to John Arbuthnot (1710), followed by Pierre-Simon Laplace (1770s), in analyzing the human sex ratio at birth; see . Modern origins and early controversy Modern significance testing is largely the product of Karl Pearson ( ''p''-value, Pearson's chi-squared test), William Sealy Gosset (Student's t-distribution), and Ronald Fisher ("null hypothesis", analysis of variance, " significance test"), while hypothesis testing was developed by Jerzy Neyman and Egon Pearson (son of Karl). Ronald Fisher began his life in statistics as a Bayesian (Zabell 1992), but Fisher soon grew disenchanted with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Realization (probability)
In probability and statistics, a realization, observation, or observed value, of a random variable is the value that is actually observed (what actually happened). The random variable itself is the process dictating how the observation comes about. Statistical quantities computed from realizations without deploying a statistical model are often called "empirical", as in empirical distribution function or empirical probability. Conventionally, to avoid confusion, upper case letters denote random variables; the corresponding lower case letters denote their realizations. Formal definition In more formal probability theory, a random variable is a function ''X'' defined from a sample space Ω to a measurable space called the state space. If an element in Ω is mapped to an element in state space by ''X'', then that element in state space is a realization. Elements of the sample space can be thought of as all the different possibilities that ''could'' happen; while a rea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Null Hypothesis
In scientific research, the null hypothesis (often denoted ''H''0) is the claim that no difference or relationship exists between two sets of data or variables being analyzed. The null hypothesis is that any experimentally observed difference is due to chance alone, and an underlying causative relationship does not exist, hence the term "null". In addition to the null hypothesis, an alternative hypothesis is also developed, which claims that a relationship does exist between two variables. Basic definitions The ''null hypothesis'' and the ''alternative hypothesis'' are types of conjectures used in statistical tests, which are formal methods of reaching conclusions or making decisions on the basis of data. The hypotheses are conjectures about a statistical model of the population, which are based on a sample of the population. The tests are core elements of statistical inference, heavily used in the interpretation of scientific experimental data, to separate scientific claims ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antithesis
Antithesis ( Greek for "setting opposite", from "against" and "placing") is used in writing or speech either as a proposition that contrasts with or reverses some previously mentioned proposition, or when two opposites are introduced together for contrasting effect. This is based on the logical phrase or term. Antithesis can be defined as "a figure of speech involving a seeming contradiction of ideas, words, clauses, or sentences within a balanced grammatical structure. Parallelism of expression serves to emphasize opposition of ideas". An antithesis must always contain two ideas within one statement. The ideas may not be structurally opposite, but they serve to be functionally opposite when comparing two ideas for emphasis. According to Aristotle, the use of an antithesis makes the audience better understand the point the speaker is trying to make. Further explained, the comparison of two situations or ideas makes choosing the correct one simpler. Aristotle states that anti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Inference
Statistical inference is the process of using data analysis to infer properties of an underlying distribution of probability.Upton, G., Cook, I. (2008) ''Oxford Dictionary of Statistics'', OUP. . Inferential statistical analysis infers properties of a population, for example by testing hypotheses and deriving estimates. It is assumed that the observed data set is sampled from a larger population. Inferential statistics can be contrasted with descriptive statistics. Descriptive statistics is solely concerned with properties of the observed data, and it does not rest on the assumption that the data come from a larger population. In machine learning, the term ''inference'' is sometimes used instead to mean "make a prediction, by evaluating an already trained model"; in this context inferring properties of the model is referred to as ''training'' or ''learning'' (rather than ''inference''), and using a model for prediction is referred to as ''inference'' (instead of ''prediction' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ronald Fisher
Sir Ronald Aylmer Fisher (17 February 1890 – 29 July 1962) was a British polymath who was active as a mathematician, statistician, biologist, geneticist, and academic. For his work in statistics, he has been described as "a genius who almost single-handedly created the foundations for modern statistical science" and "the single most important figure in 20th century statistics". In genetics, his work used mathematics to combine Mendelian genetics and natural selection; this contributed to the revival of Darwinism in the early 20th-century revision of the theory of evolution known as the modern synthesis. For his contributions to biology, Fisher has been called "the greatest of Darwin’s successors". Fisher held strong views on race and eugenics, insisting on racial differences. Although he was clearly a eugenist and advocated for the legalization of voluntary sterilization of those with heritable mental disabilities, there is some debate as to whether Fisher supported ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neyman–Pearson Lemma
In statistics, the Neyman–Pearson lemma was introduced by Jerzy Neyman and Egon Pearson in a paper in 1933. The Neyman-Pearson lemma is part of the Neyman-Pearson theory of statistical testing, which introduced concepts like errors of the second kind, power function, and inductive behavior.The Fisher, Neyman-Pearson Theories of Testing Hypotheses: One Theory or Two?: Journal of the American Statistical Association: Vol 88, No 424The Fisher, Neyman-Pearson Theories of Testing Hypotheses: One Theory or Two?: Journal of the American Statistical Association: Vol 88, No 424/ref>Wald: Chapter II: The Neyman-Pearson Theory of Testing a Statistical HypothesisWald: Chapter II: The Neyman-Pearson Theory of Testing a Statistical Hypothesis/ref>The Empire of ChanceThe Empire of Chance/ref> The previous Fisherian theory of significance testing postulated only one hypothesis. By introducing a competing hypothesis, the Neyman-Pearsonian flavor of statistical testing allows investigating the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Egon Pearson
Egon Sharpe Pearson (11 August 1895 – 12 June 1980) was one of three children of Karl Pearson and Maria, née Sharpe, and, like his father, a leading British statistician. Career He was educated at Winchester College and Trinity College, Cambridge, and succeeded his father as professor of statistics at University College London and as editor of the journal ''Biometrika''. Pearson is best known for development of the Neyman–Pearson lemma of statistical hypothesis testing. He was elected a Fellow of the Econometric Society in 1948. He was President of the Royal Statistical Society in 1955–56, and was awarded its Guy Medal in gold in 1955. He was appointed a CBE in 1946. He was elected a Fellow of the Royal Society in March 1966. His candidacy citation read: Family life Pearson married Eileen Jolly in 1934 and the couple had two daughters, Judith and Sarah. Eileen died of pneumonia in 1949. Pearson subsequently married Margaret Theodosia Scott in 1967 and the coup ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jerzy Neyman
Jerzy Neyman (April 16, 1894 – August 5, 1981; born Jerzy Spława-Neyman; ) was a Polish mathematician and statistician who spent the first part of his professional career at various institutions in Warsaw, Poland and then at University College London, and the second part at the University of California, Berkeley. Neyman first introduced the modern concept of a confidence interval into statistical hypothesis testing and co-revised Ronald Fisher's null hypothesis testing (in collaboration with Egon Pearson). Life and career He was born into a Polish family in Bendery, in the Bessarabia Governorate of the Russian Empire, the fourth of four children of Czesław Spława-Neyman and Kazimiera Lutosławska. His family was Roman Catholic and Neyman served as an altar boy during his early childhood. Later, Neyman would become an agnostic. Neyman's family descended from a long line of Polish nobles and military heroes. He graduated from the Kamieniec Podolski gubernial gymnasium for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
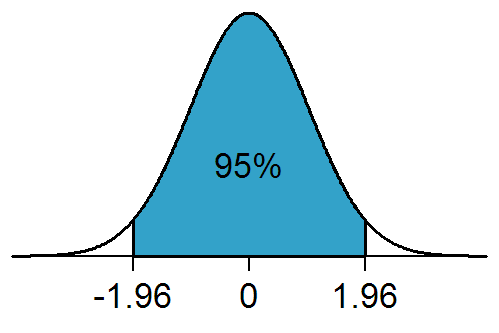
Significance Level
In statistical hypothesis testing, a result has statistical significance when it is very unlikely to have occurred given the null hypothesis (simply by chance alone). More precisely, a study's defined significance level, denoted by \alpha, is the probability of the study rejecting the null hypothesis, given that the null hypothesis is true; and the ''p''-value of a result, ''p'', is the probability of obtaining a result at least as extreme, given that the null hypothesis is true. The result is statistically significant, by the standards of the study, when p \le \alpha. The significance level for a study is chosen before data collection, and is typically set to 5% or much lower—depending on the field of study. In any experiment or observation that involves drawing a sample from a population, there is always the possibility that an observed effect would have occurred due to sampling error alone. But if the ''p''-value of an observed effect is less than (or equal to) the significan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
P-value
In null-hypothesis significance testing, the ''p''-value is the probability of obtaining test results at least as extreme as the result actually observed, under the assumption that the null hypothesis is correct. A very small ''p''-value means that such an extreme observed outcome would be very unlikely under the null hypothesis. Reporting ''p''-values of statistical tests is common practice in academic publications of many quantitative fields. Since the precise meaning of ''p''-value is hard to grasp, misuse is widespread and has been a major topic in metascience. Basic concepts In statistics, every conjecture concerning the unknown probability distribution of a collection of random variables representing the observed data X in some study is called a ''statistical hypothesis''. If we state one hypothesis only and the aim of the statistical test is to see whether this hypothesis is tenable, but not to investigate other specific hypotheses, then such a test is called a null ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
T Distribution .
{{disambig ...
The phrase "T distribution" may refer to * Student's t-distribution in univariate probability theory, * Hotelling's T-square distribution in multivariate statistics. * Multivariate Student distribution In statistics, the multivariate ''t''-distribution (or multivariate Student distribution) is a multivariate probability distribution. It is a generalization to random vectors of the Student's t-distribution, Student's ''t''-distribution, which i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
