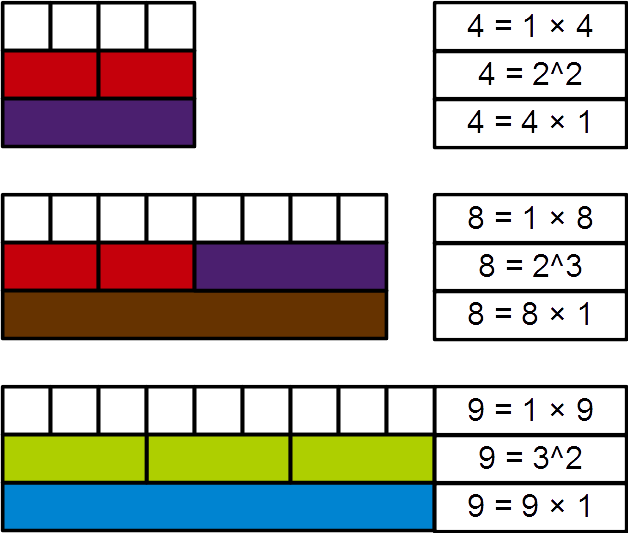
|
Achilles Number
An Achilles number is a number that is powerful but not a perfect power. A positive integer is a powerful number if, for every prime factor of , is also a divisor. In other words, every prime factor appears at least squared in the factorization. All Achilles numbers are powerful. However, not all powerful numbers are Achilles numbers: only those that cannot be represented as , where and are positive integers greater than 1. Achilles numbers were named by Henry Bottomley after Achilles, a hero of the Trojan war, who was also powerful but imperfect. ''Strong Achilles numbers'' are Achilles numbers whose Euler totients are also Achilles numbers. Sequence of Achilles numbers A number is powerful if . If in addition the number is an Achilles number. The Achilles numbers up to 5000 are: :72, 108, 200, 288, 392, 432, 500, 648, 675, 800, 864, 968, 972, 1125, 1152, 1323, 1352, 1372, 1568, 1800, 1944, 2000, 2312, 2592, 2700, 2888, 3087, 3200, 3267, 3456, 3528, 3872, 3888, 40 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Achilles Number Cuisenaire Rods 72
In Greek mythology, Achilles ( ) or Achilleus ( grc-gre, Ἀχιλλεύς) was a hero of the Trojan War, the greatest of all the Greek warriors, and the central character of Homer's ''Iliad''. He was the son of the Nereid Thetis and Peleus, king of Phthia. Achilles' most notable feat during the Trojan War was the slaying of the Trojan prince Hector outside the gates of Troy. Although the death of Achilles is not presented in the ''Iliad'', other sources concur that he was killed near the end of the Trojan War by Paris, who shot him with an arrow. Later legends (beginning with Statius' unfinished epic ''Achilleid'', written in the 1st century AD) state that Achilles was invulnerable in all of his body except for one heel, because when his mother Thetis dipped him in the river Styx as an infant, she held him by one of his heels. Alluding to these legends, the term "Achilles' heel" has come to mean a point of weakness, especially in someone or something with an otherwise strong c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Powerful Number
A powerful number is a positive integer ''m'' such that for every prime number ''p'' dividing ''m'', ''p''2 also divides ''m''. Equivalently, a powerful number is the product of a square and a cube, that is, a number ''m'' of the form ''m'' = ''a''2''b''3, where ''a'' and ''b'' are positive integers. Powerful numbers are also known as squareful, square-full, or 2-full. Paul Erdős and George Szekeres studied such numbers and Solomon W. Golomb named such numbers ''powerful''. The following is a list of all powerful numbers between 1 and 1000: :1, 4, 8, 9, 16, 25, 27, 32, 36, 49, 64, 72, 81, 100, 108, 121, 125, 128, 144, 169, 196, 200, 216, 225, 243, 256, 288, 289, 324, 343, 361, 392, 400, 432, 441, 484, 500, 512, 529, 576, 625, 648, 675, 676, 729, 784, 800, 841, 864, 900, 961, 968, 972, 1000, ... . Equivalence of the two definitions If ''m'' = ''a''2''b''3, then every prime in the prime factorization of ''a'' appears in the prime factorization of ''m'' with an exponent of at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perfect Power
In mathematics, a perfect power is a natural number that is a product of equal natural factors, or, in other words, an integer that can be expressed as a square or a higher integer power of another integer greater than one. More formally, ''n'' is a perfect power if there exist natural numbers ''m'' > 1, and ''k'' > 1 such that ''mk'' = ''n''. In this case, ''n'' may be called a perfect ''k''th power. If ''k'' = 2 or ''k'' = 3, then ''n'' is called a perfect square or perfect cube, respectively. Sometimes 0 and 1 are also considered perfect powers (0''k'' = 0 for any ''k'' > 0, 1''k'' = 1 for any ''k''). Examples and sums A sequence of perfect powers can be generated by iterating through the possible values for ''m'' and ''k''. The first few ascending perfect powers in numerical order (showing duplicate powers) are : : 2^2 = 4,\ 2^3 = 8,\ 3^2 = 9,\ 2^4 = 16,\ 4^2 = 16,\ 5^2 = 25,\ 3^3 = 27, 2^5 = 32,\ 6^2 = 36,\ 7^2 = 49,\ 2^6 = 64,\ 4^3 = 64,\ 8^2 = 64, \dots The sum of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Factor
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, or , involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order. The property of being prime is called primality. A simple but slow method of checking the primality of a given number n, called trial division, tests whether n is a multiple of any integer between 2 and \sqrt. Faster algorithms include the Miller–Rabin primality test, which is fast but has a small chance of error, and the AKS primality test, which alwa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer m that may be multiplied by some integer to produce n. In this case, one also says that n is a multiple of m. An integer n is divisible or evenly divisible by another integer m if m is a divisor of n; this implies dividing n by m leaves no remainder. Definition An integer is divisible by a nonzero integer if there exists an integer such that n=km. This is written as :m\mid n. Other ways of saying the same thing are that divides , is a divisor of , is a factor of , and is a multiple of . If does not divide , then the notation is m\not\mid n. Usually, is required to be nonzero, but is allowed to be zero. With this convention, m \mid 0 for every nonzero integer . Some definitions omit the requirement that m be nonzero. General Divisors can be negative as well as positive, although sometimes the term is restricted to positive divisors. For example, there are six divisors of 4; they a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Henry Bottomley
Henry may refer to: People *Henry (given name) *Henry (surname) * Henry Lau, Canadian singer and musician who performs under the mononym Henry Royalty * Portuguese royalty ** King-Cardinal Henry, King of Portugal ** Henry, Count of Portugal, Henry of Burgundy, Count of Portugal (father of Portugal's first king) ** Prince Henry the Navigator, Infante of Portugal ** Infante Henrique, Duke of Coimbra (born 1949), the sixth in line to Portuguese throne * King of Germany **Henry the Fowler (876–936), first king of Germany * King of Scots (in name, at least) ** Henry Stuart, Lord Darnley (1545/6–1567), consort of Mary, queen of Scots ** Henry Benedict Stuart, the 'Cardinal Duke of York', brother of Bonnie Prince Charlie, who was hailed by Jacobites as Henry IX * Four kings of Castile: ** Henry I of Castile ** Henry II of Castile **Henry III of Castile ** Henry IV of Castile * Five kings of France, spelt ''Henri'' in Modern French since the Renaissance to italianize the name ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Achilles
In Greek mythology, Achilles ( ) or Achilleus ( grc-gre, Ἀχιλλεύς) was a hero of the Trojan War, the greatest of all the Greek warriors, and the central character of Homer's '' Iliad''. He was the son of the Nereid Thetis and Peleus, king of Phthia. Achilles' most notable feat during the Trojan War was the slaying of the Trojan prince Hector outside the gates of Troy. Although the death of Achilles is not presented in the ''Iliad'', other sources concur that he was killed near the end of the Trojan War by Paris, who shot him with an arrow. Later legends (beginning with Statius' unfinished epic '' Achilleid'', written in the 1st century AD) state that Achilles was invulnerable in all of his body except for one heel, because when his mother Thetis dipped him in the river Styx as an infant, she held him by one of his heels. Alluding to these legends, the term "Achilles' heel" has come to mean a point of weakness, especially in someone or something with an other ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trojan War
In Greek mythology, the Trojan War was waged against the city of Troy by the Achaeans (Greeks) after Paris of Troy took Helen from her husband Menelaus, king of Sparta. The war is one of the most important events in Greek mythology and has been narrated through many works of Greek literature, most notably Homer's ''Iliad''. The core of the ''Iliad'' (Books II – XXIII) describes a period of four days and two nights in the tenth year of the decade-long siege of Troy; the '' Odyssey'' describes the journey home of Odysseus, one of the war's heroes. Other parts of the war are described in a cycle of epic poems, which have survived through fragments. Episodes from the war provided material for Greek tragedy and other works of Greek literature, and for Roman poets including Virgil and Ovid. The ancient Greeks believed that Troy was located near the Dardanelles and that the Trojan War was a historical event of the 13th or 12th century BC, but by the mid-19th century AD, both ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler Totient
In number theory, Euler's totient function counts the positive integers up to a given integer that are relatively prime to . It is written using the Greek letter phi as \varphi(n) or \phi(n), and may also be called Euler's phi function. In other words, it is the number of integers in the range for which the greatest common divisor is equal to 1. The integers of this form are sometimes referred to as totatives of . For example, the totatives of are the six numbers 1, 2, 4, 5, 7 and 8. They are all relatively prime to 9, but the other three numbers in this range, 3, 6, and 9 are not, since and . Therefore, . As another example, since for the only integer in the range from 1 to is 1 itself, and . Euler's totient function is a multiplicative function, meaning that if two numbers and are relatively prime, then . This function gives the order of the multiplicative group of integers modulo (the group of unit (ring theory), units of the ring (algebra), ring \Z/n\Z). It ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Powerful Number
A powerful number is a positive integer ''m'' such that for every prime number ''p'' dividing ''m'', ''p''2 also divides ''m''. Equivalently, a powerful number is the product of a square and a cube, that is, a number ''m'' of the form ''m'' = ''a''2''b''3, where ''a'' and ''b'' are positive integers. Powerful numbers are also known as squareful, square-full, or 2-full. Paul Erdős and George Szekeres studied such numbers and Solomon W. Golomb named such numbers ''powerful''. The following is a list of all powerful numbers between 1 and 1000: :1, 4, 8, 9, 16, 25, 27, 32, 36, 49, 64, 72, 81, 100, 108, 121, 125, 128, 144, 169, 196, 200, 216, 225, 243, 256, 288, 289, 324, 343, 361, 392, 400, 432, 441, 484, 500, 512, 529, 576, 625, 648, 675, 676, 729, 784, 800, 841, 864, 900, 961, 968, 972, 1000, ... . Equivalence of the two definitions If ''m'' = ''a''2''b''3, then every prime in the prime factorization of ''a'' appears in the prime factorization of ''m'' with an exponent of at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Greatest Common Divisor
In mathematics, the greatest common divisor (GCD) of two or more integers, which are not all zero, is the largest positive integer that divides each of the integers. For two integers ''x'', ''y'', the greatest common divisor of ''x'' and ''y'' is denoted \gcd (x,y). For example, the GCD of 8 and 12 is 4, that is, \gcd (8, 12) = 4. In the name "greatest common divisor", the adjective "greatest" may be replaced by "highest", and the word "divisor" may be replaced by "factor", so that other names include highest common factor (hcf), etc. Historically, other names for the same concept have included greatest common measure. This notion can be extended to polynomials (see Polynomial greatest common divisor) and other commutative rings (see below). Overview Definition The ''greatest common divisor'' (GCD) of two nonzero integers and is the greatest positive integer such that is a divisor of both and ; that is, there are integers and such that and , and is the larges ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Factorization
In number theory, integer factorization is the decomposition of a composite number into a product of smaller integers. If these factors are further restricted to prime numbers, the process is called prime factorization. When the numbers are sufficiently large, no efficient non-quantum integer factorization algorithm is known. However, it has not been proven that such an algorithm does not exist. The presumed difficulty of this problem is important for the algorithms used in cryptography such as RSA public-key encryption and the RSA digital signature. Many areas of mathematics and computer science have been brought to bear on the problem, including elliptic curves, algebraic number theory, and quantum computing. In 2019, Fabrice Boudot, Pierrick Gaudry, Aurore Guillevic, Nadia Heninger, Emmanuel Thomé and Paul Zimmermann factored a 240-digit (795-bit) number ( RSA-240) utilizing approximately 900 core-years of computing power. The researchers estimated that a 1024-bit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |