|
Asymptotic Dimension
In analytic geometry, an asymptote () of a curve is a line such that the distance between the curve and the line approaches zero as one or both of the ''x'' or ''y'' coordinates tends to infinity. In projective geometry and related contexts, an asymptote of a curve is a line which is tangent to the curve at a point at infinity. The word asymptote is derived from the Greek ἀσύμπτωτος (''asumptōtos'') which means "not falling together", from ἀ priv. + σύν "together" + πτωτ-ός "fallen". The term was introduced by Apollonius of Perga in his work on conic sections, but in contrast to its modern meaning, he used it to mean any line that does not intersect the given curve. There are three kinds of asymptotes: ''horizontal'', ''vertical'' and ''oblique''. For curves given by the graph of a function , horizontal asymptotes are horizontal lines that the graph of the function approaches as ''x'' tends to Vertical asymptotes are vertical lines near which th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Line (geometry)
In geometry, a straight line, usually abbreviated line, is an infinitely long object with no width, depth, or curvature, an idealization of such physical objects as a straightedge, a taut string, or a ray (optics), ray of light. Lines are space (mathematics), spaces of dimension one, which may be Embedding, embedded in spaces of dimension two, three, or higher. The word ''line'' may also refer, in everyday life, to a line segment, which is a part of a line delimited by two Point (geometry), points (its ''endpoints''). Euclid's Elements, Euclid's ''Elements'' defines a straight line as a "breadthless length" that "lies evenly with respect to the points on itself", and introduced several postulates as basic unprovable properties on which the rest of geometry was established. ''Euclidean line'' and ''Euclidean geometry'' are terms introduced to avoid confusion with generalizations introduced since the end of the 19th century, such as Non-Euclidean geometry, non-Euclidean, Project ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logistic Function
A logistic function or logistic curve is a common S-shaped curve ( sigmoid curve) with the equation f(x) = \frac where The logistic function has domain the real numbers, the limit as x \to -\infty is 0, and the limit as x \to +\infty is L. The exponential function with negated argument (e^ ) is used to define the standard logistic function, depicted at right, where L=1, k=1, x_0=0, which has the equation f(x) = \frac and is sometimes simply called the sigmoid. It is also sometimes called the expit, being the inverse function of the logit. The logistic function finds applications in a range of fields, including biology (especially ecology), biomathematics, chemistry, demography, economics, geoscience, mathematical psychology, probability, sociology, political science, linguistics, statistics, and artificial neural networks. There are various generalizations, depending on the field. History The logistic function was introduced in a series of three papers by Pier ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Error Function
In mathematics, the error function (also called the Gauss error function), often denoted by , is a function \mathrm: \mathbb \to \mathbb defined as: \operatorname z = \frac\int_0^z e^\,\mathrm dt. The integral here is a complex Contour integration, contour integral which is path-independent because \exp(-t^2) is Holomorphic function, holomorphic on the whole complex plane \mathbb. In many applications, the function argument is a real number, in which case the function value is also real. In some old texts, the error function is defined without the factor of \frac. This nonelementary integral is a sigmoid function, sigmoid function that occurs often in probability, statistics, and partial differential equations. In statistics, for non-negative real values of , the error function has the following interpretation: for a real random variable that is normal distribution, normally distributed with mean 0 and standard deviation \frac, is the probability that falls in the range . ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
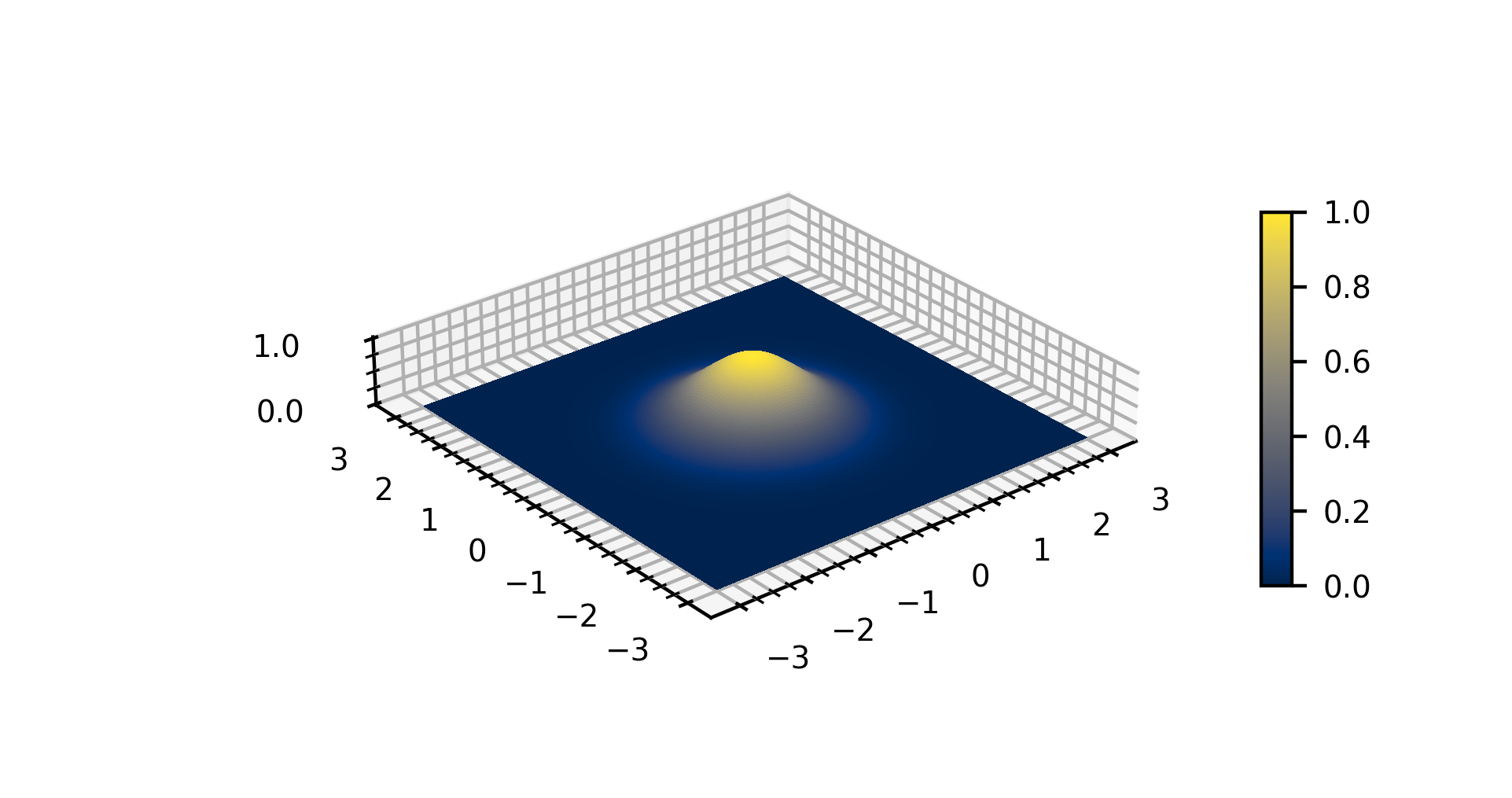
Gaussian Function
In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function (mathematics), function of the base form f(x) = \exp (-x^2) and with parametric extension f(x) = a \exp\left( -\frac \right) for arbitrary real number, real constants , and non-zero . It is named after the mathematician Carl Friedrich Gauss. The graph of a function, graph of a Gaussian is a characteristic symmetric "Normal distribution, bell curve" shape. The parameter is the height of the curve's peak, is the position of the center of the peak, and (the standard deviation, sometimes called the Gaussian Root mean square, RMS width) controls the width of the "bell". Gaussian functions are often used to represent the probability density function of a normal distribution, normally distributed random variable with expected value and variance . In this case, the Gaussian is of the form g(x) = \frac \exp\left( -\frac \frac \right). Gaussian functions are widely used in statistics to describ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbola
In mathematics, a hyperbola is a type of smooth function, smooth plane curve, curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected component (topology), connected components or branches, that are mirror images of each other and resemble two infinite bow (weapon), bows. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane (mathematics), plane and a double cone (geometry), cone. (The other conic sections are the parabola and the ellipse. A circle is a special case of an ellipse.) If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola. Besides being a conic section, a hyperbola can arise as the locus (mathematics), locus of points whose difference of distances to two fixed focus (geometry), foci is constant, as a curve for each point of which the rays to two fix ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arctangent
In mathematics, the inverse trigonometric functions (occasionally also called ''antitrigonometric'', ''cyclometric'', or ''arcus'' functions) are the inverse functions of the trigonometric functions, under suitably restricted domains. Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the angle's trigonometric ratios. Inverse trigonometric functions are widely used in engineering, navigation, physics, and geometry. Notation Several notations for the inverse trigonometric functions exist. The most common convention is to name inverse trigonometric functions using an arc- prefix: , , , etc. (This convention is used throughout this article.) This notation arises from the following geometric relationships: when measuring in radians, an angle of radians will correspond to an arc whose length is , where is the radius of the circle. Thus in the unit circle, the cosine of x f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Asymptote03
In analytic geometry, an asymptote () of a curve is a line such that the distance between the curve and the line approaches zero as one or both of the ''x'' or ''y'' coordinates tends to infinity. In projective geometry and related contexts, an asymptote of a curve is a line which is tangent to the curve at a point at infinity. The word asymptote is derived from the Greek ἀσύμπτωτος (''asumptōtos'') which means "not falling together", from ἀ priv. + σύν "together" + πτωτ-ός "fallen". The term was introduced by Apollonius of Perga in his work on conic sections, but in contrast to its modern meaning, he used it to mean any line that does not intersect the given curve. There are three kinds of asymptotes: ''horizontal'', ''vertical'' and ''oblique''. For curves given by the graph of a function , horizontal asymptotes are horizontal lines that the graph of the function approaches as ''x'' tends to Vertical asymptotes are vertical lines near which the fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
One-sided Limit
In calculus, a one-sided limit refers to either one of the two Limit of a function, limits of a Function (mathematics), function f(x) of a Real number, real variable x as x approaches a specified point either from the left or from the right. The limit as x decreases in value approaching a (x approaches a "from the right" or "from above") can be denoted: \lim_f(x) \quad \text \quad \lim_\,f(x) \quad \text \quad \lim_\,f(x) \quad \text \quad f(x+) The limit as x increases in value approaching a (x approaches a "from the left" or "from below") can be denoted: \lim_f(x) \quad \text \quad \lim_\, f(x) \quad \text \quad \lim_\,f(x) \quad \text \quad f(x-) If the limit of f(x) as x approaches a exists then the limits from the left and from the right both exist and are equal. In some cases in which the limit \lim_ f(x) does not exist, the two one-sided limits nonetheless exist. Consequently, the limit as x approaches a is sometimes called a "two-sided limit". It is possible for exa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Function
In mathematics, a continuous function is a function such that a small variation of the argument induces a small variation of the value of the function. This implies there are no abrupt changes in value, known as '' discontinuities''. More precisely, a function is continuous if arbitrarily small changes in its value can be assured by restricting to sufficiently small changes of its argument. A discontinuous function is a function that is . Until the 19th century, mathematicians largely relied on intuitive notions of continuity and considered only continuous functions. The epsilon–delta definition of a limit was introduced to formalize the definition of continuity. Continuity is one of the core concepts of calculus and mathematical analysis, where arguments and values of functions are real and complex numbers. The concept has been generalized to functions between metric spaces and between topological spaces. The latter are the most general continuous functions, and their d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertical Line Test
In mathematics, the vertical line test is a visual way to determine if a curve is a graph of a function or not. A function can only have one output, ''y'', for each unique input, ''x''. If a vertical line intersects a curve on an ''xy''-plane more than once then for one value of ''x'' the curve has more than one value of ''y'', and so, the curve does not represent a function. If all vertical lines intersect a curve at most once then the curve represents a function. See also *Horizontal line test In mathematics, the horizontal line test is a test used to determine whether a function is injective (i.e., one-to-one). In calculus A ''horizontal line'' is a straight, flat line that goes from left to right. Given a function f \colon \mathbb \t ... Notes {{Reflist Functions and mappings ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |