|
Astroid (manga)
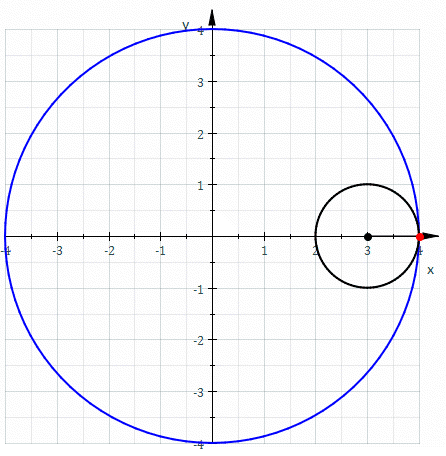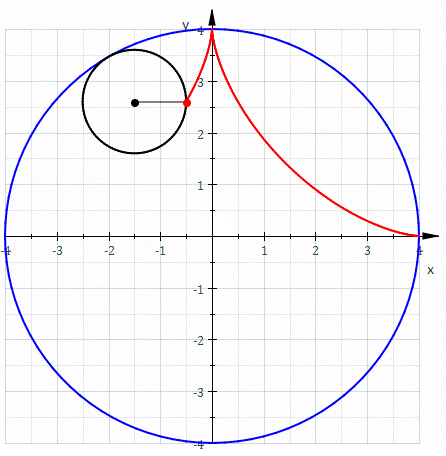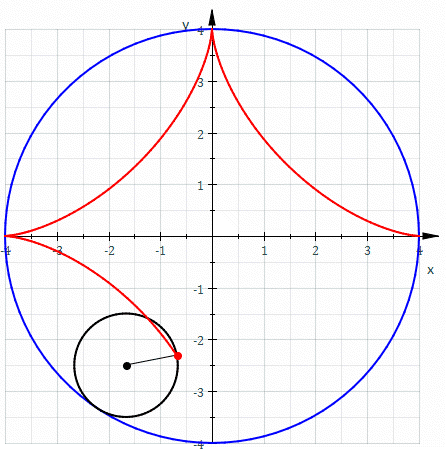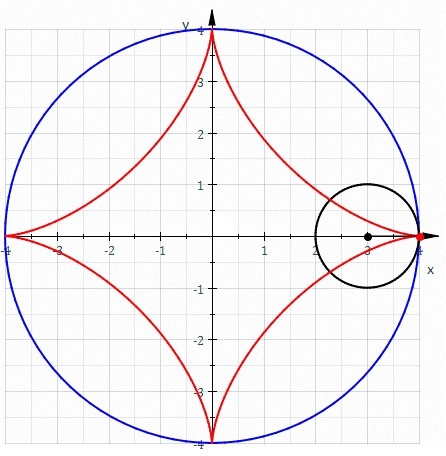
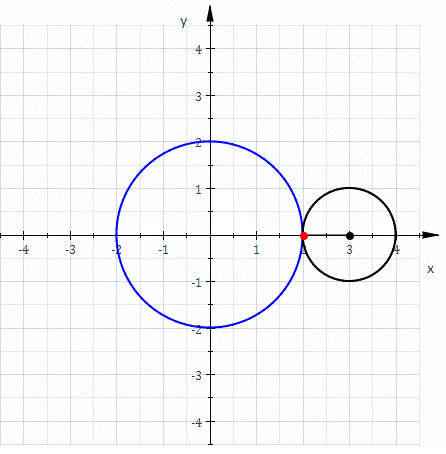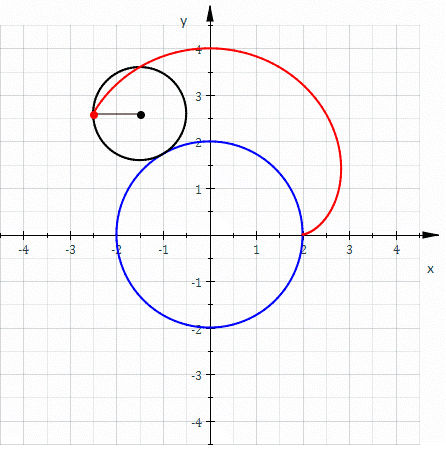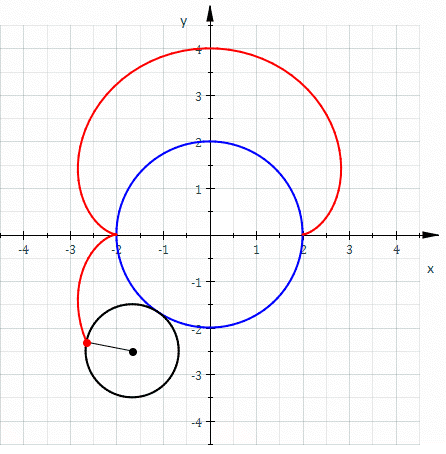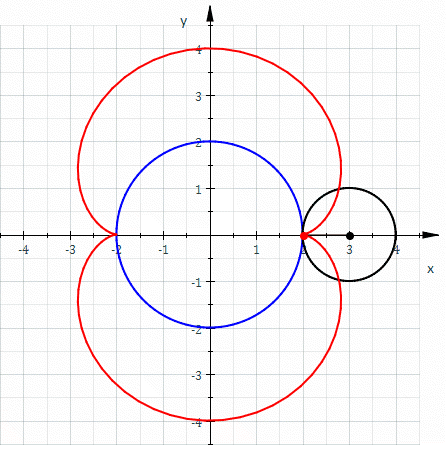
In mathematics, an astroid is a particular type of roulette curve: a hypocycloid with four cusps. Specifically, it is the locus of a point on a circle as it rolls inside a fixed circle with four times the radius. By double generation, it is also the locus of a point on a circle as it rolls inside a fixed circle with 4/3 times the radius. It can also be defined as the envelope of a line segment of fixed length that moves while keeping an end point on each of the axes. It is therefore the envelope of the moving bar in the Trammel of Archimedes. Its modern name comes from the Greek word for "star". It was proposed, originally in the form of "Astrois", by Joseph Johann von Littrow in 1838. The curve had a variety of names, including tetracuspid (still used), cubocycloid, and paracycle. It is nearly identical in form to the evolute of an ellipse. Equations If the radius of the fixed circle is ''a'' then the equation is given by x^ + y^ = a^. This implies that an astroid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Astroid
In mathematics, an astroid is a particular type of roulette curve: a hypocycloid with four cusps. Specifically, it is the locus of a point on a circle as it rolls inside a fixed circle with four times the radius. By double generation, it is also the locus of a point on a circle as it rolls inside a fixed circle with 4/3 times the radius. It can also be defined as the envelope of a line segment of fixed length that moves while keeping an end point on each of the axes. It is therefore the envelope of the moving bar in the Trammel of Archimedes. Its modern name comes from the Greek word for "star". It was proposed, originally in the form of "Astrois", by Joseph Johann von Littrow in 1838. The curve had a variety of names, including tetracuspid (still used), cubocycloid, and paracycle. It is nearly identical in form to the evolute of an ellipse. Equations If the radius of the fixed circle is ''a'' then the equation is given by :x^ + y^ = a^. \, This implies that an astroid is al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parametric Equation
In mathematics, a parametric equation defines a group of quantities as functions of one or more independent variables called parameters. Parametric equations are commonly used to express the coordinates of the points that make up a geometric object such as a curve or surface, in which case the equations are collectively called a parametric representation or parameterization (alternatively spelled as parametrisation) of the object. For example, the equations :\begin x &= \cos t \\ y &= \sin t \end form a parametric representation of the unit circle, where ''t'' is the parameter: A point (''x'', ''y'') is on the unit circle if and only if there is a value of ''t'' such that these two equations generate that point. Sometimes the parametric equations for the individual scalar output variables are combined into a single parametric equation in vectors: :(x, y)=(\cos t, \sin t). Parametric representations are generally nonunique (see the "Examples in two dimensions" section belo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Deltoid Curve
In geometry, a deltoid curve, also known as a tricuspoid curve or Steiner curve, is a hypocycloid of three cusps. In other words, it is the roulette created by a point on the circumference of a circle as it rolls without slipping along the inside of a circle with three or one-and-a-half times its radius. It is named after the capital Greek letter delta (Δ) which it resembles. More broadly, a ''deltoid'' can refer to any closed figure with three vertices connected by curves that are concave to the exterior, making the interior points a non-convex set. Equations A hypocycoid can be represented (up to rotation and translation) by the following parametric equations :x=(b-a)\cos(t)+a\cos\left(\fracat\right) \, :y=(b-a)\sin(t)-a\sin\left(\fracat\right) \, , where ''a'' is the radius of the rolling circle, ''b'' is the radius of the circle within which the aforementioned circle is rolling. (In the illustration above ''b = 3a'' tracing the deltoid.) In complex coordinates this bec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nephroid
In geometry, a nephroid () is a specific plane curve. It is a type of epicycloid in which the smaller circle's radius differs from the larger by a factor of one-half. Name Although the term ''nephroid'' was used to describe other curves, it was applied to the curve in this article by Richard A. Proctor in 1878. Strict definition A nephroid is * an algebraic curve of degree 6. * an epicycloid with two cusps * a plane simple closed curve = a Jordan curve Equations Parametric If the small circle has radius a, the fixed circle has midpoint (0,0) and radius 2a, the rolling angle of the small circle is 2\varphi and point (2a,0) the starting point (see diagram) then one gets the parametric representation: :x(\varphi) = 3a\cos\varphi- a\cos3\varphi=6a\cos\varphi-4a \cos^3\varphi \ , :y(\varphi) = 3a \sin\varphi - a\sin3\varphi =4a\sin^3\varphi\ , \qquad 0\le \varphi < 2\pi The complex map maps the unit circle to a nephroid [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cardioid
In geometry, a cardioid () is a plane curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. It can also be defined as an epicycloid having a single cusp. It is also a type of sinusoidal spiral, and an inverse curve of the parabola with the focus as the center of inversion. A cardioid can also be defined as the set of points of reflections of a fixed point on a circle through all tangents to the circle. The name was coined by de Castillon in 1741 but the cardioid had been the subject of study decades beforehand.Yates Named for its heart-like form, it is shaped more like the outline of the cross section of a round apple without the stalk. A cardioid microphone exhibits an acoustic pickup pattern that, when graphed in two dimensions, resembles a cardioid (any 2d plane containing the 3d straight line of the microphone body). In three dimensions, the cardioid is shaped like an apple centred around the microphone which is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hedgehog (geometry)
In differential geometry, a hedgehog or plane hedgehog is a type of plane curve, the envelope of a family of lines determined by a support function. More intuitively, sufficiently well-behaved hedgehogs are plane curves with one tangent line in each oriented direction. A projective hedgehog is a restricted type of hedgehog, defined from an anti-symmetric support function, and (again when sufficiently well-behaved) forms a curve with one tangent line in each direction, regardless of orientation. Every closed strictly convex curve, the envelope of its supporting lines. The astroid forms a non-convex hedgehog, and the deltoid curve forms a projective hedgehog. Hedgehogs can also be defined from support functions of hyperplanes in higher dimensions. Definitions Formally, a planar support function can be defined as a continuously differentiable function h from the unit circle in the plane to real numbers, or equivalently as a function f(\theta)=h\bigl((\cos\theta,\sin\theta)\bigr) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Evolute
In the differential geometry of curves, the evolute of a curve is the locus of all its centers of curvature. That is to say that when the center of curvature of each point on a curve is drawn, the resultant shape will be the evolute of that curve. The evolute of a circle is therefore a single point at its center. Equivalently, an evolute is the envelope of the normals to a curve. The evolute of a curve, a surface, or more generally a submanifold, is the caustic of the normal map. Let be a smooth, regular submanifold in . For each point in and each vector , based at and normal to , we associate the point . This defines a Lagrangian map, called the normal map. The caustic of the normal map is the evolute of . Evolutes are closely connected to involutes: A curve is the evolute of any of its involutes. History Apollonius ( 200 BC) discussed evolutes in Book V of his ''Conics''. However, Huygens is sometimes credited with being the first to study them (1673). Huygens ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cruciform Curve
In algebraic geometry, a quartic plane curve is a plane algebraic curve of the fourth degree of a polynomial, degree. It can be defined by a bivariate quartic equation: :Ax^4+By^4+Cx^3y+Dx^2y^2+Exy^3+Fx^3+Gy^3+Hx^2y+Ixy^2+Jx^2+Ky^2+Lxy+Mx+Ny+P=0, with at least one of not equal to zero. This equation has 15 constants. However, it can be multiplied by any non-zero constant without changing the curve; thus by the choice of an appropriate constant of multiplication, any one of the coefficients can be set to 1, leaving only 14 constants. Therefore, the space of quartic curves can be identified with the real projective space It also follows, from Cramer's theorem (algebraic curves), Cramer's theorem on algebraic curves, that there is exactly one quartic curve that passes through a set of 14 distinct points in general position, since a quartic has 14 Degrees of freedom (physics and chemistry), degrees of freedom. A quartic curve can have a maximum of: * Four connected components * Tw ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dual Curve
In projective geometry, a dual curve of a given plane curve is a curve in the dual projective plane consisting of the set of lines tangent to . There is a map from a curve to its dual, sending each point to the point dual to its tangent line. If is algebraic then so is its dual and the degree of the dual is known as the ''class'' of the original curve. The equation of the dual of , given in line coordinates, is known as the ''tangential equation'' of . Duality is an involution: the dual of the dual of is the original curve . The construction of the dual curve is the geometrical underpinning for the Legendre transformation in the context of Hamiltonian mechanics. Equations Let be the equation of a curve in homogeneous coordinates on the projective plane. Let be the equation of a line, with being designated its line coordinatesin a dual projective plane. The condition that the line is tangent to the curve can be expressed in the form which is the tangential equation of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometric Genus
In algebraic geometry, the geometric genus is a basic birational invariant of algebraic varieties and complex manifolds. Definition The geometric genus can be defined for non-singular complex projective varieties and more generally for complex manifolds as the Hodge number (equal to by Serre duality), that is, the dimension of the canonical linear system plus one. In other words for a variety of complex dimension it is the number of linearly independent holomorphic -forms to be found on .Danilov & Shokurov (1998), p. 53/ref> This definition, as the dimension of : then carries over to any base field, when is taken to be the sheaf of Kähler differentials and the power is the (top) exterior power, the canonical line bundle. The geometric genus is the first invariant of a sequence of invariants called the plurigenera. Case of curves In the case of complex varieties, (the complex loci of) non-singular curves are Riemann surfaces. The algebraic definition of genus agre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Curve
In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane curve can be completed in a projective algebraic plane curve by homogenizing its defining polynomial. Conversely, a projective algebraic plane curve of homogeneous equation can be restricted to the affine algebraic plane curve of equation . These two operations are each inverse to the other; therefore, the phrase algebraic plane curve is often used without specifying explicitly whether it is the affine or the projective case that is considered. More generally, an algebraic curve is an algebraic variety of dimension one. Equivalently, an algebraic curve is an algebraic variety that is birationally equivalent to an algebraic plane curve. If the curve is contained in an affine space or a projective space, one can take a projection for such a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polar Coordinate System
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The reference point (analogous to the origin of a Cartesian coordinate system) is called the ''pole'', and the ray from the pole in the reference direction is the ''polar axis''. The distance from the pole is called the ''radial coordinate'', ''radial distance'' or simply ''radius'', and the angle is called the ''angular coordinate'', ''polar angle'', or ''azimuth''. Angles in polar notation are generally expressed in either degrees or radians (2 rad being equal to 360°). Grégoire de Saint-Vincent and Bonaventura Cavalieri independently introduced the concepts in the mid-17th century, though the actual term "polar coordinates" has been attributed to Gregorio Fontana in the 18th century. The initial motivation for the introduction of the polar system was the study of circula ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |