|
Arc Elasticity
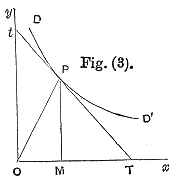
In mathematics and economics, the arc elasticity is the elasticity of one variable with respect to another between two given points. It is the ratio of the percentage change of one of the variables between the two points to the percentage change of the other variable. It contrasts with the ''point elasticity'', which is the limit of the arc elasticity as the distance between the two points approaches zero and which hence is defined at a single point rather than for a pair of points. Formula The ''y'' arc elasticity of ''x'' is defined as: :E_ = \frac where the percentage change in going from point 1 to point 2 is usually calculated relative to the midpoint: :\% \mbox x = \frac; :\% \mbox y = \frac. The use of the midpoint arc elasticity formula (with the midpoint used for the base of the change, rather than the initial point (''x''1, ''y''1) which is used in almost all other contexts for calculating percentages) was advocated by R. G. D. Allen for use when ''x'' refers to the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Economics
Economics () is a behavioral science that studies the Production (economics), production, distribution (economics), distribution, and Consumption (economics), consumption of goods and services. Economics focuses on the behaviour and interactions of Agent (economics), economic agents and how economy, economies work. Microeconomics analyses what is viewed as basic elements within economy, economies, including individual agents and market (economics), markets, their interactions, and the outcomes of interactions. Individual agents may include, for example, households, firms, buyers, and sellers. Macroeconomics analyses economies as systems where production, distribution, consumption, savings, and Expenditure, investment expenditure interact; and the factors of production affecting them, such as: Labour (human activity), labour, Capital (economics), capital, Land (economics), land, and Entrepreneurship, enterprise, inflation, economic growth, and public policies that impact gloss ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elasticity (mathematics)
In mathematics, the elasticity or point elasticity of a positive differentiable function ''f'' of a positive variable (positive input, positive output) at point ''a'' is defined as :Ef(a) = \fracf'(a) :=\lim_\frac\frac=\lim_\frac\frac=\lim_\frac\approx \frac or equivalently :Ef(x) = \frac. It is thus the ratio of the relative (percentage) change in the function's output f(x) with respect to the relative change in its input x, for infinitesimal changes from a point (a, f(a)). Equivalently, it is the ratio of the infinitesimal change of the logarithm of a function with respect to the infinitesimal change of the logarithm of the argument. Generalizations to multi-input–multi-output cases also exist in the literature. The elasticity of a function is a constant \alpha if and only if the function has the form f(x) = C x ^ \alpha for a constant C>0. The elasticity at a point is the limit of the arc elasticity between two points as the separation between those two points approaches zero ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Percentage Change
In any quantitative science, the terms relative change and relative difference are used to compare two quantities while taking into account the "sizes" of the things being compared, i.e. dividing by a ''standard'' or ''reference'' or ''starting'' value. The comparison is expressed as a ratio and is a unitless number. By multiplying these ratios by 100 they can be expressed as percentages so the terms percentage change, percent(age) difference, or relative percentage difference are also commonly used. The terms "change" and "difference" are used interchangeably. Relative change is often used as a quantitative indicator of quality assurance and quality control for repeated measurements where the outcomes are expected to be the same. A special case of percent change (relative change expressed as a percentage) called '' percent error'' occurs in measuring situations where the reference value is the accepted or actual value (perhaps theoretically determined) and the value being comp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Review Of Economic Studies
''The Review of Economic Studies'' (also known as ''REStud'') is a quarterly peer-reviewed academic journal covering economics. The journal is widely considered one of the top 5 journals in economics. It is managed by the editorial board currently chaired by Ruben Enikolopov. The current joint managing editors are Thomas Chaney at University of Southern California, Xavier D’Haultfoeuille at Center for Research in Economics and Statistics, Andrea Galeotti at London Business School, Bard Harstad at Stanford Graduate School of Business, Nir Jaimovich at University of California, San Diego, Katrine Loken at Norwegian School of Economics, Elias Papaioannou at London Business School, Vincent Sterk at University College London, and Noam Yuchtman at University of Oxford. According to the ''Journal Citation Reports'', the journal has a 2020 impact factor of 6.345. History The journal was founded in 1933 by a group of economists based in Britain and the United States. The original editori ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Price Elasticity Of Demand
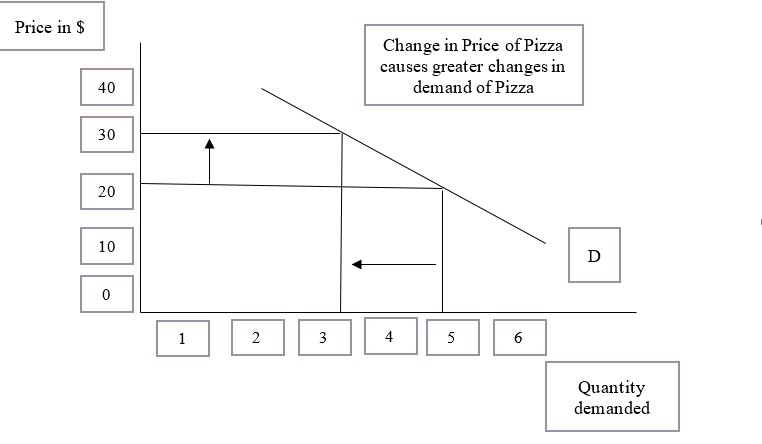
A good's price elasticity of demand (E_d, PED) is a measure of how sensitive the quantity demanded is to its price. When the price rises, quantity demanded falls for almost any good ( law of demand), but it falls more for some than for others. The price elasticity gives the percentage change in quantity demanded when there is a one percent increase in price, holding everything else constant. If the elasticity is −2, that means a one percent price rise leads to a two percent decline in quantity demanded. Other elasticities measure how the quantity demanded changes with other variables (e.g. the income elasticity of demand for consumer income changes). Price elasticities are negative except in special cases. If a good is said to have an elasticity of 2, it almost always means that the good has an elasticity of −2 according to the formal definition. The phrase "more elastic" means that a good's elasticity has greater magnitude, ignoring the sign. Veblen and Giffen goods are t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elasticity Of A Function
In mathematics, the elasticity or point elasticity of a positive differentiable function ''f'' of a positive variable (positive input, positive output) at point ''a'' is defined as :Ef(a) = \fracf'(a) :=\lim_\frac\frac=\lim_\frac\frac=\lim_\frac\approx \frac or equivalently :Ef(x) = \frac. It is thus the ratio of the relative (percentage) change in the function's output f(x) with respect to the relative change in its input x, for infinitesimal changes from a point (a, f(a)). Equivalently, it is the ratio of the infinitesimal change of the logarithm of a function with respect to the infinitesimal change of the logarithm of the argument. Generalizations to multi-input–multi-output cases also exist in the literature. The elasticity of a function is a constant \alpha if and only if the function has the form f(x) = C x ^ \alpha for a constant C>0. The elasticity at a point is the limit of the arc elasticity between two points as the separation between those two points approaches zer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elasticity (economics)
In economics, elasticity measures the responsiveness of one economic variable to a change in another. For example, if the price elasticity of the demand of a good is −2, then a 10% increase in price will cause the quantity demanded to fall by 20%. Elasticity in economics provides an understanding of changes in the behavior of the buyers and sellers with price changes. There are two types of elasticity for demand and supply, one is inelastic demand and supply and the other one is elastic demand and supply. Introduction The concept of price elasticity was first cited in an informal form in the book ''Principles of Economics (Marshall book), Principles of Economics'' published by the author Alfred Marshall in 1890. Subsequently, a major study of the price elasticity of supply and the price elasticity of demand for US products was undertaken by Joshua Levy and Trevor Pollock in the late 1960s. Elasticity is an important concept in neoclassical economic theory, and enables in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |