|
Anharmonicity
In classical mechanics, anharmonicity is the deviation of a system from being a harmonic oscillator. An oscillator that is not oscillating in harmonic motion is known as an anharmonic oscillator where the system can be approximated to a harmonic oscillator and the anharmonicity can be calculated using perturbation theory. If the anharmonicity is large, then other numerical techniques have to be used. In reality all oscillating systems are anharmonic, but most approximate the harmonic oscillator the smaller the amplitude of the oscillation is. As a result, oscillations with frequencies 2\omega and 3\omega etc., where \omega is the fundamental frequency of the oscillator, appear. Furthermore, the frequency \omega deviates from the frequency \omega_0 of the harmonic oscillations. See also intermodulation and combination tones. As a first approximation, the frequency shift \Delta \omega=\omega-\omega_0 is proportional to the square of the oscillation amplitude A: :\Delta \omeg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inharmonicity
In music, inharmonicity is the degree to which the frequency, frequencies of overtones (also known as Harmonic series (music)#Partial, partials or partial tones) depart from Integer, whole multiples of the fundamental frequency (harmonic series (music), harmonic series). Acoustically, a note perceived to have a single distinct pitch in fact contains a variety of additional overtones. Many percussion instruments, such as cymbals, tam-tams, and Tubular bells, chimes, create complex and inharmonic sounds. Music harmony and intonation depends strongly on the harmonicity of tones. An ideal, homogeneous, infinitesimally thin or infinitely flexible string or column of air has exact harmonic modes of vibration. In any real musical instrument, the resonant body that produces the music tone—typically a string, wire, or column of air—deviates from this ideal and has some small or large amount of inharmonicity. For instance, a very thick string behaves less as an ideal string and m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonlinear Resonance
In physics, nonlinear resonance is the occurrence of resonance in a nonlinear system. In nonlinear resonance the system behaviour – resonance frequency, resonance frequencies and normal mode, modes – depends on the amplitude of the oscillations, while for linear systems this is independent of amplitude. The mixing of modes in non-linear systems is termed resonant interaction. Description Generically two types of resonances have to be distinguished – linear and nonlinear. From the physical point of view, they are defined by whether or not external force coincides with the natural frequency, eigen-frequency of the system (linear and nonlinear resonance correspondingly). Vibrational modes can interact in a resonant interaction when both the energy and momentum of the interacting modes is conserved. The conservation of energy implies that the sum of the frequencies of the modes must sum to zero: : \omega_n=\omega_+ \omega_+ \cdots + \omega_, with possibly different \omega_i=\o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonic Oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force ''F'' proportional to the displacement ''x'': \vec F = -k \vec x, where ''k'' is a positive constant. The harmonic oscillator model is important in physics, because any mass subject to a force in stable equilibrium acts as a harmonic oscillator for small vibrations. Harmonic oscillators occur widely in nature and are exploited in many manmade devices, such as clocks and radio circuits. If ''F'' is the only force acting on the system, the system is called a simple harmonic oscillator, and it undergoes simple harmonic motion: sinusoidal oscillations about the equilibrium point, with a constant amplitude and a constant frequency (which does not depend on the amplitude). If a frictional force ( damping) proportional to the velocity is also present, the harmonic oscillator is described as a damped oscillator. Depending on the friction ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonic Oscillators
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force ''F'' proportional to the displacement ''x'': \vec F = -k \vec x, where ''k'' is a positive constant. The harmonic oscillator model is important in physics, because any mass subject to a force in stable equilibrium acts as a harmonic oscillator for small vibrations. Harmonic oscillators occur widely in nature and are exploited in many manmade devices, such as clocks and radio circuits. If ''F'' is the only force acting on the system, the system is called a simple harmonic oscillator, and it undergoes simple harmonic motion: sinusoidal oscillations about the equilibrium point, with a constant amplitude and a constant frequency (which does not depend on the amplitude). If a frictional force (damping) proportional to the velocity is also present, the harmonic oscillator is described as a damped oscillator. Depending on the friction coef ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Superharmonic
An overtone is any resonant frequency above the fundamental frequency of a sound. (An overtone may or may not be a harmonic) In other words, overtones are all pitches higher than the lowest pitch within an individual sound; the fundamental is the lowest pitch. While the fundamental is usually heard most prominently, overtones are actually present in any pitch except a true sine wave. The relative volume or amplitude of various overtone partials is one of the key identifying features of timbre, or the individual characteristic of a sound. Using the model of Fourier analysis, the fundamental and the overtones together are called partials. Harmonics, or more precisely, harmonic partials, are partials whose frequencies are numerical integer multiples of the fundamental (including the fundamental, which is 1 times itself). These overlapping terms are variously used when discussing the acoustic behavior of musical instruments. Alexander J. Ellis (translating Hermann von Helmholtz) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Møller–Plesset Perturbation Theory
Møller–Plesset perturbation theory (MP) is one of several quantum chemistry post-Hartree–Fock ab initio methods in the field of computational chemistry. It improves on the Hartree–Fock method by adding electron correlation effects by means of Rayleigh–Schrödinger perturbation theory (RS-PT), usually to second (MP2), third (MP3) or fourth (MP4) order. Its main idea was published as early as 1934 by Christian Møller and Milton S. Plesset. Rayleigh–Schrödinger perturbation theory The MP perturbation theory is a special case of RS perturbation theory. In RS theory one considers an unperturbed Hamiltonian operator \hat_, to which a small (often external) perturbation \hat is added: :\hat = \hat_ + \lambda \hat. Here, ''λ'' is an arbitrary real parameter that controls the size of the perturbation. In MP theory the zeroth-order wave function is an exact eigenfunction of the Fock operator, which thus serves as the unperturbed operator. The perturbation is the c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean-field Theory
In physics and probability theory, Mean-field theory (MFT) or Self-consistent field theory studies the behavior of high-dimensional random (stochastic) models by studying a simpler model that approximates the original by averaging over Degrees of freedom (statistics), degrees of freedom (the number of values in the final calculation of a statistic that are free to vary). Such models consider many individual components that interact with each other. The main idea of MFT is to replace all fundamental interaction, interactions to any one body with an average or effective interaction, sometimes called a ''molecular field''. This reduces any many-body problem into an effective one-body problem. The ease of solving MFT problems means that some insight into the behavior of the system can be obtained at a lower computational cost. MFT has since been applied to a wide range of fields outside of physics, including statistical inference, graphical models, neuroscience, artificial intelligenc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
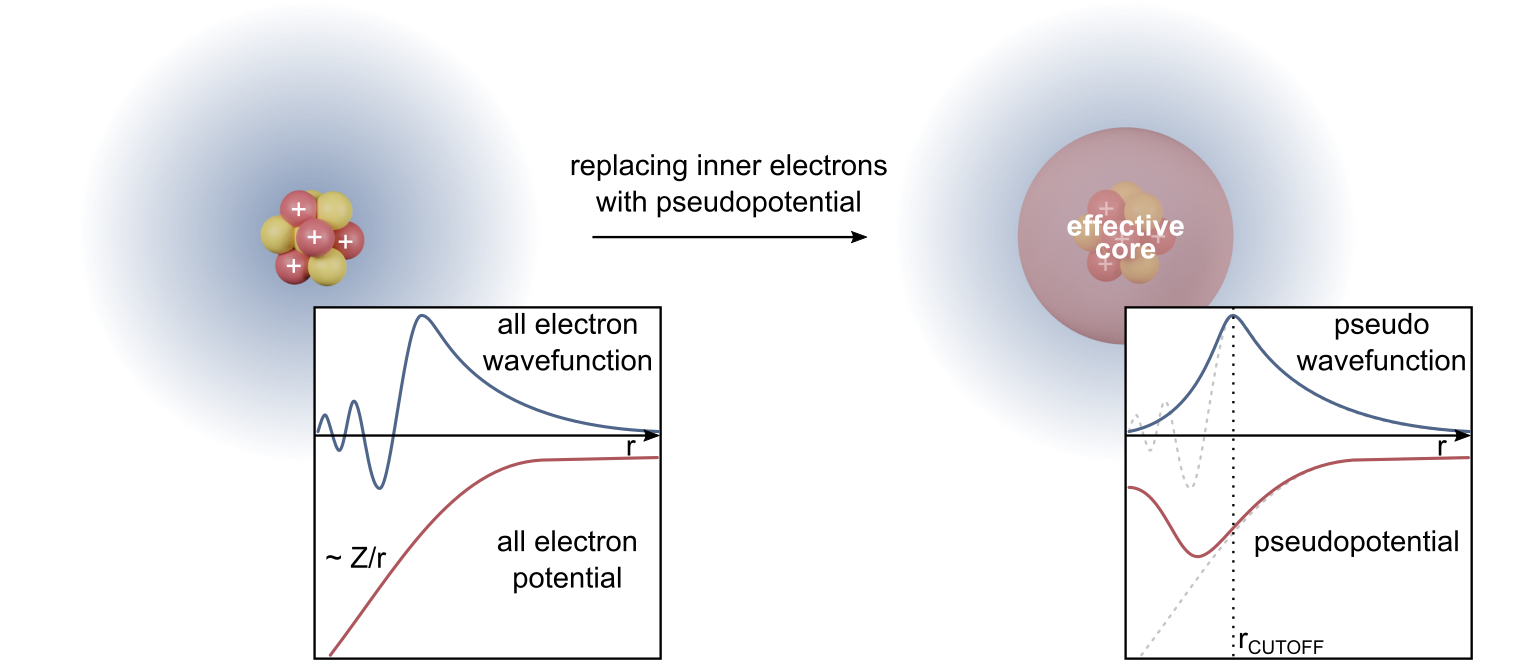
Density-functional Theory
Density functional theory (DFT) is a computational quantum mechanics, quantum mechanical modelling method used in physics, chemistry and materials science to investigate the electronic structure (or nuclear structure) (principally the ground state) of Many-body problem, many-body systems, in particular atoms, molecules, and the condensed phases. Using this theory, the properties of a many-electron system can be determined by using Functional (mathematics), functionals - that is, functions that accept a function as input and output a single real number. In the case of DFT, these are functionals of the spatially dependent electronic density, electron density. DFT is among the most popular and versatile methods available in condensed-matter physics, computational physics, and computational chemistry. DFT has been very popular for calculations in solid-state physics since the 1970s. However, DFT was not considered accurate enough for calculations in quantum chemistry until the 1990 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quasi-harmonic Approximation
The quasi-harmonic approximation is a phonon-based model of solid-state physics used to describe volume-dependent thermal effects, such as the thermal expansion. It is based on the assumption that the harmonic approximation holds for every value of the lattice constant, which is to be viewed as an adjustable parameter. Overview The quasi-harmonic approximation expands upon the harmonic phonon model of lattice dynamics. The harmonic phonon model states that all interatomic forces are purely harmonic, but such a model is inadequate to explain thermal expansion, as the equilibrium distance between atoms in such a model is independent of temperature. Thus in the quasi-harmonic model, from a phonon point of view, phonon frequencies become volume-dependent in the quasi-harmonic approximation, such that for each volume, the harmonic approximation holds. Thermodynamics For a lattice, the Helmholtz free energy ''F'' in the quasi-harmonic approximation is F(T,V) = E_(V) + U_(T,V) - T S ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Acoustics
Acoustics is a branch of physics that deals with the study of mechanical waves in gases, liquids, and solids including topics such as vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics technology may be called an Acoustical engineering, acoustical engineer. The application of acoustics is present in almost all aspects of modern society with the most obvious being the audio and noise control industries. Hearing (sense), Hearing is one of the most crucial means of survival in the animal world and speech is one of the most distinctive characteristics of human development and culture. Accordingly, the science of acoustics spreads across many facets of human society—music, medicine, architecture, industrial production, warfare and more. Likewise, animal species such as songbirds and frogs use sound and hearing as a key element of mating rituals or for marking territories. Art, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
String (music)
In music, strings are long flexible structures on string instruments that produce sound through vibration. Strings are held under tension so that they can vibrate freely. The pitch (frequency) at which a string will vibrate is primarily related to its vibrating length (also called speaking length), its tension, and its mass per unit of length. A vibrating string produces very little sound by itself. Therefore, most string instruments have a soundboard to amplify the sound. There are two main kinds of strings; plain and wound. "Plain" strings are simply one piece of long cylindrical material, commonly consisted of nylon or gut. "Wound" strings have a central core, with other material being tightly wound around the string . Prior to World War II, strings of many instruments (including violins and guitars) were composed of a material known as catgut, a type of cord made from refined natural fibers of animal intestines. During the mid-twentieth century however, steel and nylo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |