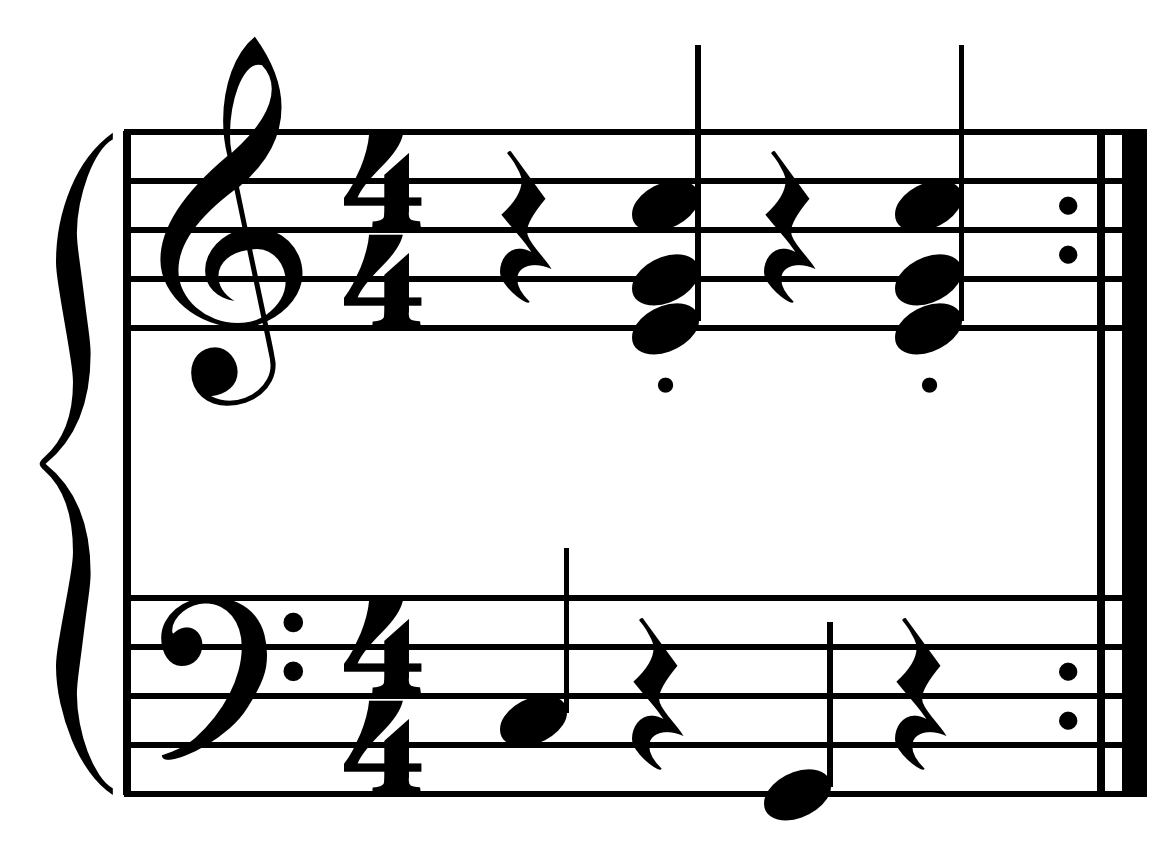|
Alternating Optimization
Alternating may refer to: Mathematics * Alternating algebra, an algebra in which odd-grade elements square to zero * Alternating form, a function formula in algebra * Alternating group, the group of even permutations of a finite set * Alternating knot, a knot or link diagram for which the crossings alternate under, over, under, over, as one travels along each component of the link * Alternating map, a multilinear map that is zero whenever any two of its arguments are equal * Alternating operator In mathematics, the exterior algebra, or Grassmann algebra, named after Hermann Grassmann, is an algebra that uses the exterior product or wedge product as its multiplication. In mathematics, the exterior product or wedge product of vectors is a ..., a multilinear map in algebra * Alternating permutation, a type of permutation studied in combinatorics * Alternating series, an infinite series in which the signs of the general terms alternate between positive and negative Elect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alternating Algebra
In mathematics, an alternating algebra is a -graded algebra for which for all nonzero homogeneous elements and (i.e. it is an anticommutative algebra) and has the further property that for every homogeneous element of odd degree. Examples * The differential forms on a differentiable manifold form an alternating algebra. * The exterior algebra is an alternating algebra. * The cohomology ring of a topological space is an alternating algebra. Properties * The algebra formed as the direct sum of the homogeneous subspaces of even degree of an anticommutative algebra is a subalgebra contained in the centre of , and is thus commutative. * An anticommutative algebra over a (commutative) base ring in which 2 is not a zero divisor is alternating. See also * Alternating multilinear map * Exterior algebra * Graded-symmetric algebra In algebra, given a commutative ring ''R'', the graded-symmetric algebra of a graded ''R''-module ''M'' is the quotient of the tensor algebra of ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alternating Form
In mathematics, the exterior algebra, or Grassmann algebra, named after Hermann Grassmann, is an algebra that uses the exterior product or wedge product as its multiplication. In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in geometry to study areas, volumes, and their higher-dimensional analogues. The exterior product of two vectors u and v, denoted by u \wedge v, is called a bivector and lives in a space called the ''exterior square'', a vector space that is distinct from the original space of vectors. The magnitude of u \wedge v can be interpreted as the area of the parallelogram with sides u and v, which in three dimensions can also be computed using the cross product of the two vectors. More generally, all parallel plane surfaces with the same orientation and area have the same bivector as a measure of their oriented area. Like the cross product, the exterior product is anticommutative, meaning tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alternating Group
In mathematics, an alternating group is the group of even permutations of a finite set. The alternating group on a set of elements is called the alternating group of degree , or the alternating group on letters and denoted by or Basic properties For , the group A''n'' is the commutator subgroup of the symmetric group S''n'' with index 2 and has therefore ''n''!/2 elements. It is the kernel of the signature group homomorphism explained under symmetric group. The group A''n'' is abelian if and only if and simple if and only if or . A5 is the smallest non-abelian simple group, having order 60, and the smallest non-solvable group. The group A4 has the Klein four-group V as a proper normal subgroup, namely the identity and the double transpositions , that is the kernel of the surjection of A4 onto . We have the exact sequence . In Galois theory, this map, or rather the corresponding map , corresponds to associating the Lagrange resolvent cubic to a quartic, which allow ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alternating Knot
In knot theory, a knot or link diagram is alternating if the crossings alternate under, over, under, over, as one travels along each component of the link. A link is alternating if it has an alternating diagram. Many of the knots with crossing number less than 10 are alternating. This fact and useful properties of alternating knots, such as the Tait conjectures, was what enabled early knot tabulators, such as Tait, to construct tables with relatively few mistakes or omissions. The simplest non-alternating prime knots have 8 crossings (and there are three such: 819, 820, 821). It is conjectured that as the crossing number increases, the percentage of knots that are alternating goes to 0 exponentially quickly. Alternating links end up having an important role in knot theory and 3-manifold theory, due to their complements having useful and interesting geometric and topological properties. This led Ralph Fox to ask, "What is an alternating knot?" By this he was asking what non-diag ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alternating Map
In mathematics, more specifically in multilinear algebra, an alternating multilinear map is a multilinear map with all arguments belonging to the same vector space (for example, a bilinear form or a multilinear form) that is zero whenever any pair of arguments is equal. More generally, the vector space may be a module over a commutative ring. The notion of alternatization (or alternatisation) is used to derive an alternating multilinear map from any multilinear map with all arguments belonging to the same space. Definition Let R be a commutative ring and V, W be modules over R. A multilinear map of the form f\colon V^n \to W is said to be alternating if it satisfies the following equivalent conditions: # whenever there exists 1 \leq i \leq n-1 such that x_i = x_ then f(x_1,\ldots,x_n) = 0.. # whenever there exists 1 \leq i \neq j \leq n such that x_i = x_j then f(x_1,\ldots,x_n) = 0.. Vector spaces Let V, W be vector spaces over the same field. Then a multilinear map of the fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alternating Operator
In mathematics, the exterior algebra, or Grassmann algebra, named after Hermann Grassmann, is an algebra that uses the exterior product or wedge product as its multiplication. In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in geometry to study areas, volumes, and their higher-dimensional analogues. The exterior product of two vectors u and v, denoted by u \wedge v, is called a bivector and lives in a space called the ''exterior square'', a vector space that is distinct from the original space of vectors. The magnitude of u \wedge v can be interpreted as the area of the parallelogram with sides u and v, which in three dimensions can also be computed using the cross product of the two vectors. More generally, all parallel plane surfaces with the same orientation and area have the same bivector as a measure of their oriented area. Like the cross product, the exterior product is anticommutative, meaning tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alternating Permutation
In combinatorial mathematics, an alternating permutation (or zigzag permutation) of the set is a permutation (arrangement) of those numbers so that each entry is alternately greater or less than the preceding entry. For example, the five alternating permutations of are: * 1, 3, 2, 4 because 1 2 < 4, * 1, 4, 2, 3 because 1 < 4 > 2 < 3, * 2, 3, 1, 4 because 2 < 3 > 1 < 4, * 2, 4, 1, 3 because 2 < 4 > 1 < 3, and * 3, 4, 1, 2 because 3 < 4 > 1 < 2. This type of permutation was first studied by |
Alternating Series
In mathematics, an alternating series is an infinite series of the form \sum_^\infty (-1)^n a_n or \sum_^\infty (-1)^ a_n with for all . The signs of the general terms alternate between positive and negative. Like any series, an alternating series converges if and only if the associated sequence of partial sums converges. Examples The geometric series 1/2 − 1/4 %2B 1/8 − 1/16 %2B %E2%8B%AF sums to 1/3. The alternating harmonic series has a finite sum but the harmonic series does not. The Mercator series provides an analytic expression of the natural logarithm: \sum_^\infty \frac x^n \;=\; \ln (1+x). The functions sine and cosine used in trigonometry can be defined as alternating series in calculus even though they are introduced in elementary algebra as the ratio of sides of a right triangle. In fact, \sin x = \sum_^\infty (-1)^n \frac, and \cos x = \sum_^\infty (-1)^n \frac . When the alternating factor is removed from these series one obtains the hyperbolic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alternating Current
Alternating current (AC) is an electric current which periodically reverses direction and changes its magnitude continuously with time in contrast to direct current (DC) which flows only in one direction. Alternating current is the form in which electric power is delivered to businesses and residences, and it is the form of electrical energy that consumers typically use when they plug kitchen appliances, televisions, fans and electric lamps into a wall socket. A common source of DC power is a battery cell in a flashlight. The abbreviations ''AC'' and ''DC'' are often used to mean simply ''alternating'' and ''direct'', as when they modify ''current'' or ''voltage''. The usual waveform of alternating current in most electric power circuits is a sine wave, whose positive half-period corresponds with positive direction of the current and vice versa. In certain applications, like guitar amplifiers, different waveforms are used, such as triangular waves or square waves. Audio a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alternating Turns
Turn-taking is a type of organization in conversation and discourse where participants speak one at a time in alternating turns. In practice, it involves processes for constructing contributions, responding to previous comments, and transitioning to a different speaker, using a variety of linguistic and non-linguistic cues. While the structure is generally universal, that is, overlapping talk is generally avoided and silence between turns is minimized, turn-taking conventions vary by culture and community. Conventions vary in many ways, such as how turns are distributed, how transitions are signaled, or how long the average gap is between turns. In many contexts, conversation turns are a valuable means to participate in social life and have been subject to competition. It is often thought that turn-taking strategies differ by gender; consequently, turn-taking has been a topic of intense examination in gender studies. While early studies supported gendered stereotypes, such as me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alternate Bass
In music, alternate bass is a performance technique on many instruments where the bass alternates between two notes, most often the root and the fifth of a triad or chord. The perfect fifth is often, but not always, played below the root, transposed down an octave creating a fourth interval. The alternation between the root note and the fifth scale degree below it creates the characteristic sound of the alternate bass. On the guitar and bass guitar this is accomplished with the right hand alternating between two or more strings, often the bottom two on the guitar. In the following example in the C major chord C is located on the fifth string while G is located on the adjacent sixth (lowest) string and in the F major chord F is located on the adjacent fourth string: Alternate bass lines are also used on the double bass in country music, bluegrass music and related genres. On the Stradella bass system commonly found on accordions, the left-hand bass-note buttons are arrange ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |