|
Affine Combination
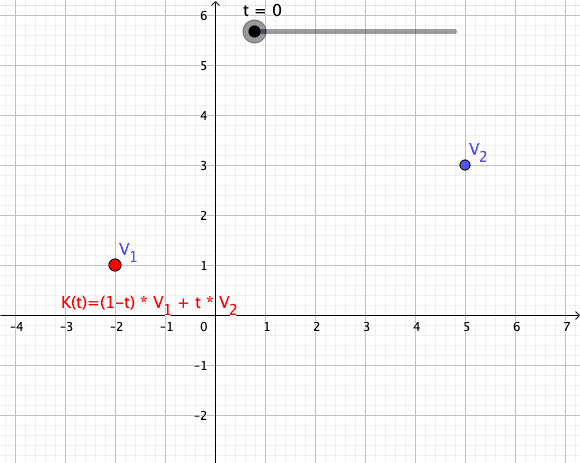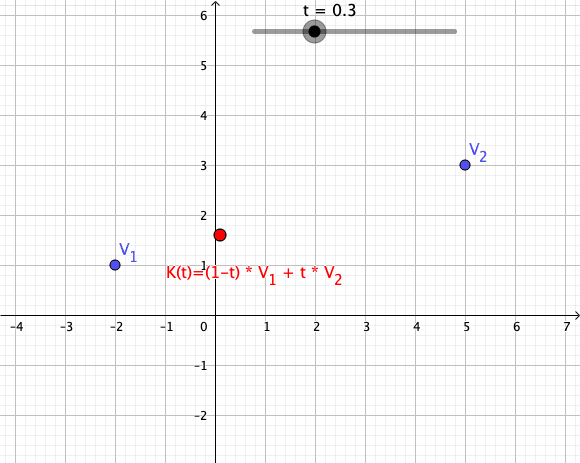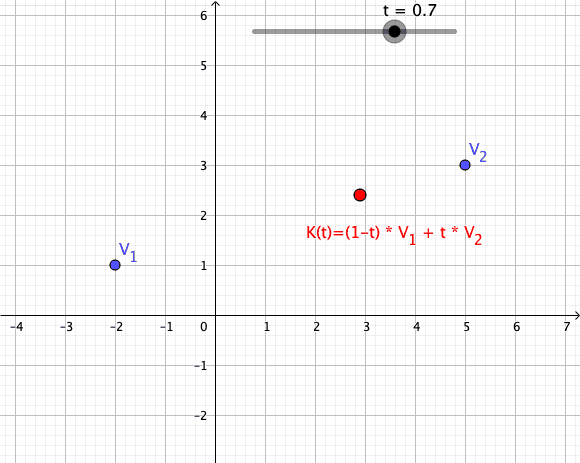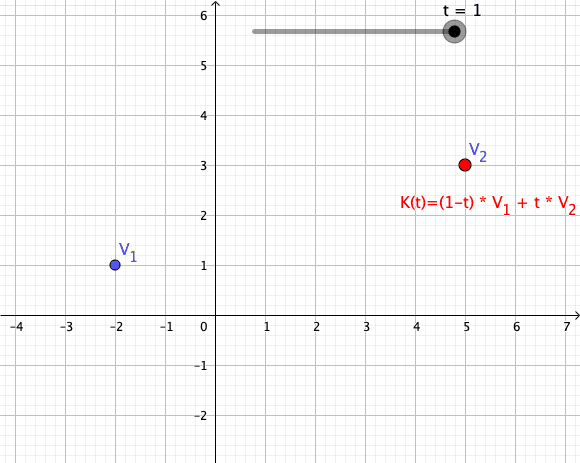
In mathematics, an affine combination of is a linear combination : \sum_^ = \alpha_ x_ + \alpha_ x_ + \cdots +\alpha_ x_, such that :\sum_^ =1. Here, can be elements ( vectors) of a vector space over a field , and the coefficients \alpha_ are elements of . The elements can also be points of a Euclidean space, and, more generally, of an affine space over a field . In this case the \alpha_ are elements of (or \mathbb R for a Euclidean space), and the affine combination is also a point. See for the definition in this case. This concept is fundamental in Euclidean geometry and affine geometry, because the set of all affine combinations of a set of points forms the smallest subspace containing the points, exactly as the linear combinations of a set of vectors form their linear span. The affine combinations commute with any affine transformation in the sense that : T\sum_^ = \sum_^. In particular, any affine combination of the fixed points of a given affine transformatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fixed Point (mathematics)
A fixed point (sometimes shortened to fixpoint, also known as an invariant point) is a value that does not change under a given transformation. Specifically, in mathematics, a fixed point of a function is an element that is mapped to itself by the function. In physics, the term fixed point can refer to a temperature that can be used as a reproducible reference point, usually defined by a phase change or triple point. Fixed point of a function Formally, is a fixed point of a function if belongs to both the domain and the codomain of , and . For example, if is defined on the real numbers by f(x) = x^2 - 3 x + 4, then 2 is a fixed point of , because . Not all functions have fixed points: for example, , has no fixed points, since is never equal to for any real number. In graphical terms, a fixed point means the point is on the line , or in other words the graph of has a point in common with that line. Fixed-point iteration In numerical analysis, ''fixed-point iter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Affine Hull
In mathematics, the affine hull or affine span of a set ''S'' in Euclidean space R''n'' is the smallest affine set containing ''S'', or equivalently, the intersection of all affine sets containing ''S''. Here, an ''affine set'' may be defined as the translation of a vector subspace. The affine hull aff(''S'') of ''S'' is the set of all affine combinations of elements of ''S'', that is, :\operatorname (S)=\left\. Examples *The affine hull of the empty set is the empty set. *The affine hull of a singleton (a set made of one single element) is the singleton itself. *The affine hull of a set of two different points is the line through them. *The affine hull of a set of three points not on one line is the plane going through them. *The affine hull of a set of four points not in a plane in R''3'' is the entire space R''3''. Properties For any subsets S, T \subseteq X * \operatorname(\operatorname S) = \operatorname S * \operatorname S is a closed set if X is finite dimensional. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Affine Geometry
In mathematics, affine geometry is what remains of Euclidean geometry when ignoring (mathematicians often say "forgetting") the metric notions of distance and angle. As the notion of ''parallel lines'' is one of the main properties that is independent of any metric, affine geometry is often considered as the study of parallel lines. Therefore, Playfair's axiom (Given a line L and a point P not on L, there is exactly one line parallel to L that passes through P.) is fundamental in affine geometry. Comparisons of figures in affine geometry are made with affine transformations, which are mappings that preserve alignment of points and parallelism of lines. Affine geometry can be developed in two ways that are essentially equivalent. In synthetic geometry, an affine space is a set of ''points'' to which is associated a set of lines, which satisfy some axioms (such as Playfair's axiom). Affine geometry can also be developed on the basis of linear algebra. In this context an affine s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Affine Space
In mathematics, an affine space is a geometric structure that generalizes some of the properties of Euclidean spaces in such a way that these are independent of the concepts of distance and measure of angles, keeping only the properties related to parallelism and ratio of lengths for parallel line segments. In an affine space, there is no distinguished point that serves as an origin. Hence, no vector has a fixed origin and no vector can be uniquely associated to a point. In an affine space, there are instead ''displacement vectors'', also called ''translation'' vectors or simply ''translations'', between two points of the space. Thus it makes sense to subtract two points of the space, giving a translation vector, but it does not make sense to add two points of the space. Likewise, it makes sense to add a displacement vector to a point of an affine space, resulting in a new point translated from the starting point by that vector. Any vector space may be viewed as an affine spa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conical Combination
Given a finite number of vectors x_1, x_2, \dots, x_n in a real vector space, a conical combination, conical sum, or weighted sum''Convex Analysis and Minimization Algorithms'' by Jean-Baptiste Hiriart-Urruty, Claude Lemaréchal, 1993, pp. 101, 102/ref>''Mathematical Programming'', by Melvyn W. Jeter (1986) p. 68/ref> of these vectors is a vector of the form : \alpha_1x_1+\alpha_2x_2+\cdots+\alpha_nx_n where \alpha_i are non-negative real numbers. The name derives from the fact that a conical sum of vectors defines a cone (possibly in a lower-dimensional subspace). Conical hull The set of all conical combinations for a given set ''S'' is called the conical hull of ''S'' and denoted ''cone''(''S'') or ''coni''(''S''). That is, :\operatorname (S)=\left\. By taking ''k'' = 0, it follows the zero vector (origin) belongs to all conical hulls (since the summation becomes an empty sum). The conical hull of a set ''S'' is a convex set. In fact, it is the intersection o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Combination
In convex geometry and vector algebra, a convex combination is a linear combination of points (which can be vectors, scalars, or more generally points in an affine space) where all coefficients are non-negative and sum to 1. In other words, the operation is equivalent to a standard weighted average, but whose weights are expressed as a percent of the total weight, instead of as a fraction of the ''count'' of the weights as in a standard weighted average. More formally, given a finite number of points x_1, x_2, \dots, x_n in a real vector space, a convex combination of these points is a point of the form :\alpha_1x_1+\alpha_2x_2+\cdots+\alpha_nx_n where the real numbers \alpha_i satisfy \alpha_i\ge 0 and \alpha_1+\alpha_2+\cdots+\alpha_n=1. As a particular example, every convex combination of two points lies on the line segment between the points. A set is convex if it contains all convex combinations of its points. The convex hull of a given set of points is identical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Matrix
In mathematics, a stochastic matrix is a square matrix used to describe the transitions of a Markov chain. Each of its entries is a nonnegative real number representing a probability. It is also called a probability matrix, transition matrix, substitution matrix, or Markov matrix. The stochastic matrix was first developed by Andrey Markov at the beginning of the 20th century, and has found use throughout a wide variety of scientific fields, including probability theory, statistics, mathematical finance and linear algebra, as well as computer science and population genetics. There are several different definitions and types of stochastic matrices: :A right stochastic matrix is a real square matrix, with each row summing to 1. :A left stochastic matrix is a real square matrix, with each column summing to 1. :A doubly stochastic matrix is a square matrix of nonnegative real numbers with each row and column summing to 1. In the same vein, one may define a stochastic vector (also ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Affine Subspace
In mathematics, an affine space is a geometric structure that generalizes some of the properties of Euclidean spaces in such a way that these are independent of the concepts of distance and measure of angles, keeping only the properties related to parallelism and ratio of lengths for parallel line segments. In an affine space, there is no distinguished point that serves as an origin. Hence, no vector has a fixed origin and no vector can be uniquely associated to a point. In an affine space, there are instead '' displacement vectors'', also called ''translation'' vectors or simply ''translations'', between two points of the space. Thus it makes sense to subtract two points of the space, giving a translation vector, but it does not make sense to add two points of the space. Likewise, it makes sense to add a displacement vector to a point of an affine space, resulting in a new point translated from the starting point by that vector. Any vector space may be viewed as an affine spa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Affine Transformation
In Euclidean geometry, an affine transformation or affinity (from the Latin, ''affinis'', "connected with") is a geometric transformation that preserves lines and parallelism, but not necessarily Euclidean distances and angles. More generally, an affine transformation is an automorphism of an affine space (Euclidean spaces are specific affine spaces), that is, a function which maps an affine space onto itself while preserving both the dimension of any affine subspaces (meaning that it sends points to points, lines to lines, planes to planes, and so on) and the ratios of the lengths of parallel line segments. Consequently, sets of parallel affine subspaces remain parallel after an affine transformation. An affine transformation does not necessarily preserve angles between lines or distances between points, though it does preserve ratios of distances between points lying on a straight line. If is the point set of an affine space, then every affine transformation on can be repre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |