|
Adhesive Category
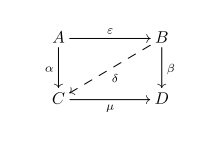
In mathematics, an adhesive category is a category where pushouts of monomorphisms exist and work more or less as they do in the category of sets. An example of an adhesive category is the category of directed multigraphs, or quivers, and the theory of adhesive categories is important in the theory of graph rewriting. More precisely, an adhesive category is one where any of the following equivalent conditions hold: * ''C'' has all pullbacks, it has pushouts along monomorphisms, and pushout squares of monomorphisms are also pullback squares and are stable under pullback. * ''C'' has all pullbacks, it has pushouts along monomorphisms, and the latter are also (bicategorical) pushouts in the bicategory of spans in ''C''. If ''C'' is small, we may equivalently say that ''C'' has all pullbacks, has pushouts along monomorphisms, and admits a full embedding into a Grothendieck topos In mathematics, a topos (, ; plural topoi or , or toposes) is a category (mathematics), category ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Category (mathematics)
In mathematics, a category (sometimes called an abstract category to distinguish it from a concrete category) is a collection of "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose objects are sets and whose arrows are functions. '' Category theory'' is a branch of mathematics that seeks to generalize all of mathematics in terms of categories, independent of what their objects and arrows represent. Virtually every branch of modern mathematics can be described in terms of categories, and doing so often reveals deep insights and similarities between seemingly different areas of mathematics. As such, category theory provides an alternative foundation for mathematics to set theory and other proposed axiomatic foundations. In general, the objects and arrows may be abstract entities of any kind, and the n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pushout (category Theory)
In category theory, a branch of mathematics, a pushout (also called a fibered coproduct or fibered sum or cocartesian square or amalgamated sum) is the colimit of a diagram consisting of two morphisms ''f'' : ''Z'' → ''X'' and ''g'' : ''Z'' → ''Y'' with a common domain. The pushout consists of an object ''P'' along with two morphisms ''X'' → ''P'' and ''Y'' → ''P'' that complete a commutative square with the two given morphisms ''f'' and ''g''. In fact, the defining universal property of the pushout (given below) essentially says that the pushout is the "most general" way to complete this commutative square. Common notations for the pushout are P = X \sqcup_Z Y and P = X +_Z Y. The pushout is the categorical dual of the pullback. Universal property Explicitly, the pushout of the morphisms ''f'' and ''g'' consists of an object ''P'' and two morphisms ''i''1 : ''X'' → ''P'' and ''i''2 : ''Y'' → ''P'' such that the diagram : commutes and such that (' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quiver (mathematics)
In graph theory, a quiver is a directed graph where Loop (graph theory), loops and multiple arrows between two vertex (graph theory), vertices are allowed, i.e. a multidigraph. They are commonly used in representation theory: a representation of a quiver assigns a vector space to each vertex of the quiver and a linear map to each arrow . In category theory, a quiver can be understood to be the underlying structure of a category (mathematics), category, but without composition or a designation of identity morphisms. That is, there is a forgetful functor from to . Its left adjoint is a free functor which, from a quiver, makes the corresponding free category. Definition A quiver Γ consists of: * The set ''V'' of vertices of Γ * The set ''E'' of edges of Γ * Two functions: ''s'': ''E'' → ''V'' giving the ''start'' or ''source'' of the edge, and another function, ''t'': ''E'' → ''V'' giving the ''target'' of the edge. This definition is identica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
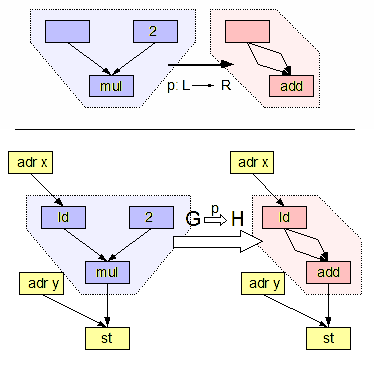
Graph Rewriting
In computer science, graph transformation, or graph rewriting, concerns the technique of creating a new graph out of an original graph algorithmically. It has numerous applications, ranging from software engineering (software construction and also software verification) to layout algorithms and picture generation. Graph transformations can be used as a computation abstraction. The basic idea is that if the state of a computation can be represented as a graph, further steps in that computation can then be represented as transformation rules on that graph. Such rules consist of an original graph, which is to be matched to a subgraph in the complete state, and a replacing graph, which will replace the matched subgraph. Formally, a graph rewriting system usually consists of a set of graph rewrite rules of the form L \rightarrow R, with L being called pattern graph (or left-hand side) and R being called replacement graph (or right-hand side of the rule). A graph rewrite rule is applie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pullback
In mathematics, a pullback is either of two different, but related processes: precomposition and fiber-product. Its dual is a pushforward. Precomposition Precomposition with a function probably provides the most elementary notion of pullback: in simple terms, a function f of a variable y, where y itself is a function of another variable x, may be written as a function of x. This is the pullback of f by the function y. f(y(x)) \equiv g(x) It is such a fundamental process that it is often passed over without mention. However, it is not just functions that can be "pulled back" in this sense. Pullbacks can be applied to many other objects such as differential forms and their cohomology classes; see * Pullback (differential geometry) * Pullback (cohomology) Fiber-product The pullback bundle is an example that bridges the notion of a pullback as precomposition, and the notion of a pullback as a Cartesian square. In that example, the base space of a fiber bundle is pulled back, in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from to is often denoted with the notation X\hookrightarrow Y. In the more general setting of category theory, a monomorphism (also called a monic morphism or a mono) is a left-cancellative morphism. That is, an arrow such that for all objects and all morphisms , : f \circ g_1 = f \circ g_2 \implies g_1 = g_2. Monomorphisms are a categorical generalization of injective functions (also called "one-to-one functions"); in some categories the notions coincide, but monomorphisms are more general, as in the examples below. The categorical dual of a monomorphism is an epimorphism, that is, a monomorphism in a category ''C'' is an epimorphism in the dual category ''C''op. Every section is a monomorphism, and every retraction is an epimorphism. Relation to invertibility Left-invertible morphisms are necessarily monic: if ''l'' is a left inverse for ''f'' (meaning ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bicategory
In mathematics, a bicategory (or a weak 2-category) is a concept in category theory used to extend the notion of category to handle the cases where the composition of morphisms is not (strictly) associative, but only associative ''up to'' an isomorphism. The notion was introduced in 1967 by Jean Bénabou. Bicategories may be considered as a weakening of the definition of 2-categories. A similar process for 3-categories leads to tricategories, and more generally to weak ''n''-categories for ''n''-categories. Definition Formally, a bicategory B consists of: * objects ''a'', ''b'', ... called 0-''cells''; * morphisms ''f'', ''g'', ... with fixed source and target objects called 1-''cells''; * "morphisms between morphisms" ρ, σ, ... with fixed source and target morphisms (which should have themselves the same source and the same target), called 2-''cells''; with some more structure: * given two objects ''a'' and ''b'' there is a category B(''a'', ''b'') whose objects are the 1- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Span (category Theory)
In category theory, a span, roof or correspondence is a generalization of the notion of relation between two objects of a category. When the category has all pullbacks (and satisfies a small number of other conditions), spans can be considered as morphisms in a category of fractions. The notion of a span is due to Nobuo Yoneda (1954) and Jean Bénabou (1967). Formal definition A span is a diagram of type \Lambda = (-1 \leftarrow 0 \rightarrow +1), i.e., a diagram of the form Y \leftarrow X \rightarrow Z. That is, let Λ be the category (-1 ← 0 → +1). Then a span in a category ''C'' is a functor ''S'' : Λ → ''C''. This means that a span consists of three objects ''X'', ''Y'' and ''Z'' of ''C'' and morphisms ''f'' : ''X'' → ''Y'' and ''g'' : ''X'' → ''Z'': it is two maps with common ''domain''. The colimit of a span is a pushout. Examples * If ''R'' is a relation between sets ''X'' and ''Y'' (i.e. a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Grothendieck Topos
In mathematics, a topos (, ; plural topoi or , or toposes) is a category that behaves like the category of sheaves of sets on a topological space (or more generally: on a site). Topoi behave much like the category of sets and possess a notion of localization; they are a direct generalization of point-set topology. The Grothendieck topoi find applications in algebraic geometry; the more general elementary topoi are used in logic. The mathematical field that studies topoi is called topos theory. Grothendieck topos (topos in geometry) Since the introduction of sheaves into mathematics in the 1940s, a major theme has been to study a space by studying sheaves on a space. This idea was expounded by Alexander Grothendieck by introducing the notion of a "topos". The main utility of this notion is in the abundance of situations in mathematics where topological heuristics are very effective, but an honest topological space is lacking; it is sometimes possible to find a topos formal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |