|
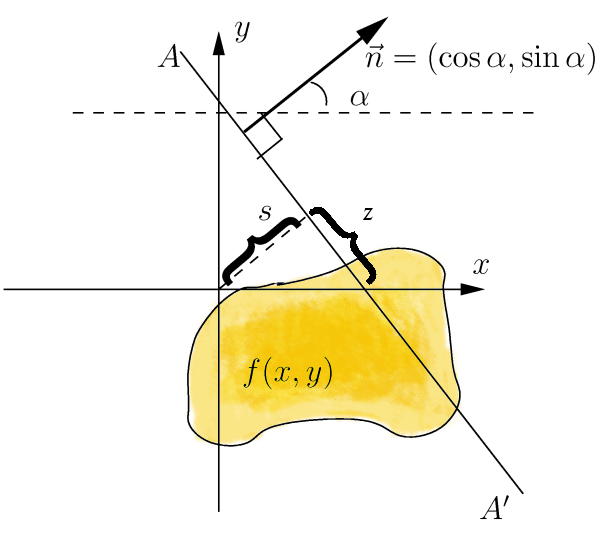
Abel Transform
In mathematics, the Abel transform,N. H. Abel, Journal für die reine und angewandte Mathematik, 1, pp. 153–157 (1826). named for Niels Henrik Abel, is an integral transform often used in the analysis of spherically symmetric or axially symmetric functions. The Abel transform of a function ''f''(''r'') is given by : F(y) = 2 \int_y^\infty \frac \,dr. Assuming that ''f''(''r'') drops to zero more quickly than 1/''r'', the inverse Abel transform is given by : f(r) = -\frac \int_r^\infty \frac \,\frac. In image analysis, the forward Abel transform is used to project an optically thin, axially symmetric emission function onto a plane, and the inverse Abel transform is used to calculate the emission function given a projection (i.e. a scan or a photograph) of that emission function. In absorption spectroscopy of cylindrical flames or plumes, the forward Abel transform is the integrated absorbance along a ray with closest distance ''y'' from the center of the flame, while the inve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differentiation Under The Integral Sign
In calculus, the Leibniz integral rule for differentiation under the integral sign, named after Gottfried Leibniz, states that for an integral of the form \int_^ f(x,t)\,dt, where -\infty < a(x), b(x) < \infty and the integral are functions dependent on the derivative of this integral is expressible as where the indicates that inside the integral, only the variation of with is considered in taking the derivative. In the special case where the functions and [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral Transforms
In mathematics, an integral transform maps a function from its original function space into another function space via integration, where some of the properties of the original function might be more easily characterized and manipulated than in the original function space. The transformed function can generally be mapped back to the original function space using the ''inverse transform''. General form An integral transform is any transform ''T'' of the following form: :(Tf)(u) = \int_^ f(t)\, K(t, u)\, dt The input of this transform is a function ''f'', and the output is another function ''Tf''. An integral transform is a particular kind of mathematical operator. There are numerous useful integral transforms. Each is specified by a choice of the function K of two variables, the kernel function, integral kernel or nucleus of the transform. Some kernels have an associated ''inverse kernel'' K^( u,t ) which (roughly speaking) yields an inverse transform: :f(t) = \int_^ (Tf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
GPS Radio Occultation
Radio occultation (RO) is a remote sensing technique used for measuring the physical properties of a planetary atmosphere or ring system. Atmospheric radio occultation Atmospheric radio occultation relies on the detection of a change in a radio signal as it passes through a planet's atmosphere, i.e. as it is occulted by the atmosphere. When electromagnetic radiation passes through the atmosphere, it is refracted (or bent). The magnitude of the refraction depends on the gradient of refractivity normal to the path, which in turn depends on the density gradient. The effect is most pronounced when the radiation traverses a long atmospheric limb path. At radio frequencies the amount of bending cannot be measured directly; instead the bending can be calculated using the Doppler shift of the signal given the geometry of the emitter and receiver. The amount of bending can be related to the refractive index by using an Abel transform on the formula relating bending angle to refractivity. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radon Transform
In mathematics, the Radon transform is the integral transform which takes a function ''f'' defined on the plane to a function ''Rf'' defined on the (two-dimensional) space of lines in the plane, whose value at a particular line is equal to the line integral of the function over that line. The transform was introduced in 1917 by Johann Radon, who also provided a formula for the inverse transform. Radon further included formulas for the transform in three dimensions, in which the integral is taken over planes (integrating over lines is known as the X-ray transform). It was later generalized to higher-dimensional Euclidean spaces, and more broadly in the context of integral geometry. The complex analogue of the Radon transform is known as the Penrose transform. The Radon transform is widely applicable to tomography, the creation of an image from the projection data associated with cross-sectional scans of an object. Explanation If a function f represents an unknown density ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projection-slice Theorem
In mathematics, the projection-slice theorem, central slice theorem or Fourier slice theorem in two dimensions states that the results of the following two calculations are equal: * Take a two-dimensional function ''f''(r), project (e.g. using the Radon transform) it onto a (one-dimensional) line, and do a Fourier transform of that projection. * Take that same function, but do a two-dimensional Fourier transform first, and then slice it through its origin, which is parallel to the projection line. In operator terms, if * ''F''1 and ''F''2 are the 1- and 2-dimensional Fourier transform operators mentioned above, * ''P''1 is the projection operator (which projects a 2-D function onto a 1-D line), * ''S''1 is a slice operator (which extracts a 1-D central slice from a function), then : F_1 P_1 = S_1 F_2. This idea can be extended to higher dimensions. This theorem is used, for example, in the analysis of medical CT scans where a "projection" is an x-ray image of an internal organ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hankel Transform
In mathematics, the Hankel transform expresses any given function ''f''(''r'') as the weighted sum of an infinite number of Bessel functions of the first kind . The Bessel functions in the sum are all of the same order ν, but differ in a scaling factor ''k'' along the ''r'' axis. The necessary coefficient of each Bessel function in the sum, as a function of the scaling factor ''k'' constitutes the transformed function. The Hankel transform is an integral transform and was first developed by the mathematician Hermann Hankel. It is also known as the Fourier–Bessel transform. Just as the Fourier transform for an infinite interval is related to the Fourier series over a finite interval, so the Hankel transform over an infinite interval is related to the Fourier–Bessel series over a finite interval. Definition The Hankel transform of order \nu of a function ''f''(''r'') is given by : F_\nu(k) = \int_0^\infty f(r) J_\nu(kr) \,r\,\mathrmr, where J_\nu is the Bessel function o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Transform
A Fourier transform (FT) is a mathematical transform that decomposes functions into frequency components, which are represented by the output of the transform as a function of frequency. Most commonly functions of time or space are transformed, which will output a function depending on temporal frequency or spatial frequency respectively. That process is also called ''analysis''. An example application would be decomposing the waveform of a musical chord into terms of the intensity of its constituent pitches. The term ''Fourier transform'' refers to both the frequency domain representation and the mathematical operation that associates the frequency domain representation to a function of space or time. The Fourier transform of a function is a complex-valued function representing the complex sinusoids that comprise the original function. For each frequency, the magnitude ( absolute value) of the complex value represents the amplitude of a constituent complex sinusoid wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projection-slice Theorem
In mathematics, the projection-slice theorem, central slice theorem or Fourier slice theorem in two dimensions states that the results of the following two calculations are equal: * Take a two-dimensional function ''f''(r), project (e.g. using the Radon transform) it onto a (one-dimensional) line, and do a Fourier transform of that projection. * Take that same function, but do a two-dimensional Fourier transform first, and then slice it through its origin, which is parallel to the projection line. In operator terms, if * ''F''1 and ''F''2 are the 1- and 2-dimensional Fourier transform operators mentioned above, * ''P''1 is the projection operator (which projects a 2-D function onto a 1-D line), * ''S''1 is a slice operator (which extracts a 1-D central slice from a function), then : F_1 P_1 = S_1 F_2. This idea can be extended to higher dimensions. This theorem is used, for example, in the analysis of medical CT scans where a "projection" is an x-ray image of an internal organ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heaviside Step Function
The Heaviside step function, or the unit step function, usually denoted by or (but sometimes , or ), is a step function, named after Oliver Heaviside (1850–1925), the value of which is zero for negative arguments and one for positive arguments. It is an example of the general class of step functions, all of which can be represented as linear combinations of translations of this one. The function was originally developed in operational calculus for the solution of differential equations, where it represents a signal that switches on at a specified time and stays switched on indefinitely. Oliver Heaviside, who developed the operational calculus as a tool in the analysis of telegraphic communications, represented the function as . The Heaviside function may be defined as: * a piecewise function: H(x) := \begin 1, & x > 0 \\ 0, & x \le 0 \end * using the Iverson bracket notation: H(x) := 0.html" ;"title=">0">>0/math> * an indicator function: H(x) := \mathbf_=\mathbf 1_(x) * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirac Delta Function
In mathematics, the Dirac delta distribution ( distribution), also known as the unit impulse, is a generalized function or distribution over the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one. The current understanding of the unit impulse is as a linear functional that maps every continuous function (e.g., f(x)) to its value at zero of its domain (f(0)), or as the weak limit of a sequence of bump functions (e.g., \delta(x) = \lim_ \frace^), which are zero over most of the real line, with a tall spike at the origin. Bump functions are thus sometimes called "approximate" or "nascent" delta distributions. The delta function was introduced by physicist Paul Dirac as a tool for the normalization of state vectors. It also has uses in probability theory and signal processing. Its validity was disputed until Laurent Schwartz developed the theory of distributions where it is defined as a linear form acting o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polymer Brush
A polymer brush is the name given to a surface coating consisting of polymers tethered to a surface. The brush may be either in a solvated state, where the tethered polymer layer consists of polymer and solvent, or in a melt state, where the tethered chains completely fill up the space available. These polymer layers can be tethered to flat substrates such as silicon wafers, or highly curved substrates such as nanoparticles. Also, polymers can be tethered in high density to another single polymer chain, although this arrangement is normally named a bottle brush. Additionally, there is a separate class of polyelectrolyte brushes, when the polymer chains themselves carry an electrostatic charge. The brushes are often characterized by the high density of grafted chains. The limited space then leads to a strong extension of the chains. Brushes can be used to stabilize colloids, reduce friction between surfaces, and to provide lubrication in artificial joint A joint or articulation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |