|
ABCD Matrix Analysis
Ray transfer matrix analysis (also known as ABCD matrix analysis) is a mathematical form for performing ray tracing calculations in sufficiently simple problems which can be solved considering only paraxial rays. Each optical element (surface, interface, mirror, or beam travel) is described by a 2×2 ''ray transfer matrix'' which operates on a vector describing an incoming light ray to calculate the outgoing ray. Multiplication of the successive matrices thus yields a concise ray transfer matrix describing the entire optical system. The same mathematics is also used in accelerator physics to track particles through the magnet installations of a particle accelerator, see electron optics. This technique, as described below, is derived using the '' paraxial approximation'', which requires that all ray directions (directions normal to the wavefronts) are at small angles ''θ'' relative to the optical axis of the system, such that the approximation \sin \theta \approx \theta rema ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ray Tracing (physics)
In physics, ray tracing is a method for calculating the path of waves or particles through a system with regions of varying propagation velocity, absorption characteristics, and reflecting surfaces. Under these circumstances, wavefronts may bend, change direction, or reflect off surfaces, complicating analysis. Ray tracing solves the problem by repeatedly advancing idealized narrow beams called ''rays'' through the medium by discrete amounts. Simple problems can be analyzed by propagating a few rays using simple mathematics. More detailed analysis can be performed by using a computer to propagate many rays. When applied to problems of electromagnetic radiation, ray tracing often relies on approximate solutions to Maxwell's equations that are valid as long as the light waves propagate through and around objects whose dimensions are much greater than the light's wavelength. Ray theory does not describe phenomena such as interference and diffraction, which require wave theory (invo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thin Lens
In optics, a thin lens is a lens with a thickness (distance along the optical axis between the two surfaces of the lens) that is negligible compared to the radii of curvature of the lens surfaces. Lenses whose thickness is not negligible are sometimes called ''thick lenses''. The thin lens approximation ignores optical effects due to the thickness of lenses and simplifies ray tracing calculations. It is often combined with the paraxial approximation in techniques such as ray transfer matrix analysis. Focal length The focal length, ''f'', of a lens in air is given by the lensmaker's equation: :\frac = (n-1) \left \frac - \frac + \frac \right where ''n'' is the index of refraction of the lens material, and ''R''1 and ''R''2 are the radii of curvature of the two surfaces. For a thin lens, ''d'' is much smaller than one of the radii of curvature (either ''R''1 or ''R''2). In these conditions, the last term of the Lensmaker's equation becomes negligible, and the focal length of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Waveguide
A waveguide is a structure that guides waves, such as electromagnetic waves or sound, with minimal loss of energy by restricting the transmission of energy to one direction. Without the physical constraint of a waveguide, wave intensities decrease according to the inverse square law as they expand into three-dimensional space. There are different types of waveguides for different types of waves. The original and most common meaningInstitute of Electrical and Electronics Engineers, “The IEEE standard dictionary of electrical and electronics terms”; 6th ed. New York, N.Y., Institute of Electrical and Electronics Engineers, c1997. IEEE Std 100-1996. d. Standards Coordinating Committee 10, Terms and Definitions; Jane Radatz, (chair)/ref> is a hollow conductive metal pipe used to carry high frequency radio waves, particularly microwaves. Dielectric waveguides are used at higher radio frequencies, and transparent dielectric waveguides and optical fibers serve as waveguides f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Curvature
In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane. For curves, the canonical example is that of a circle, which has a curvature equal to the reciprocal of its radius. Smaller circles bend more sharply, and hence have higher curvature. The curvature ''at a point'' of a differentiable curve is the curvature of its osculating circle, that is the circle that best approximates the curve near this point. The curvature of a straight line is zero. In contrast to the tangent, which is a vector quantity, the curvature at a point is typically a scalar quantity, that is, it is expressed by a single real number. For surfaces (and, more generally for higher-dimensional manifolds), that are embedded in a Euclidean space, the concept of curvature is more complex, as it depends on the choice of a direction on the surface or man ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
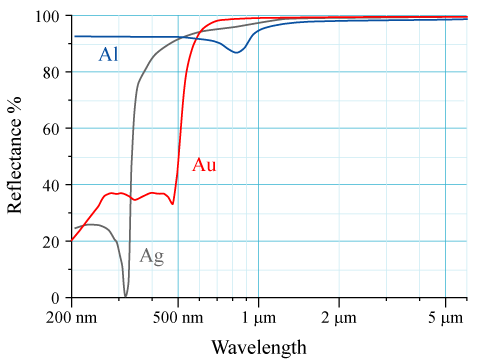
Reflectivity
The reflectance of the surface of a material is its effectiveness in reflecting radiant energy. It is the fraction of incident electromagnetic power that is reflected at the boundary. Reflectance is a component of the response of the electronic structure of the material to the electromagnetic field of light, and is in general a function of the frequency, or wavelength, of the light, its polarization, and the angle of incidence. The dependence of reflectance on the wavelength is called a ''reflectance spectrum'' or ''spectral reflectance curve''. Mathematical definitions Hemispherical reflectance The ''hemispherical reflectance'' of a surface, denoted , is defined as R = \frac, where is the radiant flux ''reflected'' by that surface and is the radiant flux ''received'' by that surface. Spectral hemispherical reflectance The ''spectral hemispherical reflectance in frequency'' and ''spectral hemispherical reflectance in wavelength'' of a surface, denoted and respectively, are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optical Resonator
An optical cavity, resonating cavity or optical resonator is an arrangement of mirrors or other optical elements that forms a cavity resonator for light waves. Optical cavities are a major component of lasers, surrounding the gain medium and providing feedback of the laser light. They are also used in optical parametric oscillators and some interferometers. Light confined in the cavity reflects multiple times, producing modes with certain resonance frequencies. Modes can be decomposed into longitudinal modes that differ only in frequency and transverse modes that have different intensity patterns across the cross-section of the beam. Many types of optical cavity produce standing wave modes. Different resonator types are distinguished by the focal lengths of the two mirrors and the distance between them. Flat mirrors are not often used because of the difficulty of aligning them to the needed precision. The geometry (resonator type) must be chosen so that the beam remains stab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometrical Optics
Geometrical optics, or ray optics, is a model of optics that describes light propagation in terms of ''rays''. The ray in geometrical optics is an abstraction useful for approximating the paths along which light propagates under certain circumstances. The simplifying assumptions of geometrical optics include that light rays: * propagate in straight-line paths as they travel in a homogeneous medium * bend, and in particular circumstances may split in two, at the interface between two dissimilar media * follow curved paths in a medium in which the refractive index changes * may be absorbed or reflected. Geometrical optics does not account for certain optical effects such as diffraction and interference. This simplification is useful in practice; it is an excellent approximation when the wavelength is small compared to the size of structures with which the light interacts. The techniques are particularly useful in describing geometrical aspects of imaging, including optical aberra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Canonical Transformation
In Hamiltonian mechanics, the linear canonical transformation (LCT) is a family of integral transforms that generalizes many classical transforms. It has 4 parameters and 1 constraint, so it is a 3-dimensional family, and can be visualized as the action of the special linear group SL2(R) on the time–frequency plane (domain). As this defines the original function up to a sign, this translates into an action of its double cover on the original function space. The LCT generalizes the Fourier, fractional Fourier, Laplace, Gauss–Weierstrass, Bargmann and the Fresnel transforms as particular cases. The name "linear canonical transformation" is from canonical transformation, a map that preserves the symplectic structure, as SL2(R) can also be interpreted as the symplectic group Sp2, and thus LCTs are the linear maps of the time–frequency domain which preserve the symplectic form, and their action on the Hilbert space is given by the Metaplectic group. The basic properties of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Beam Expander
Beam expanders are optical devices that take a collimated beam of light and expand its size (or, used in reverse, reduce its size). In laser physics they are used either as intracavity or extracavity elements. They can be telescopic in nature or prismatic. Generally prismatic beam expanders use several prisms and are known as multiple-prism beam expanders. Telescopic beam expanders include refracting and reflective telescopes. A refracting telescope commonly used is the Galilean telescope which can function as a simple beam expander for collimated light. The main advantage of the Galilean design is that it never focuses a collimated beam to a point, so effects associated with high power density such as dielectric breakdown are more avoidable than with focusing designs such as the Keplerian telescope. When used as intracavity beam expanders, in laser resonators, these telescopes provide two-dimensional beam expansion in the 20–50 range. In tunable laser resonators intracav ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional Fourier Transform
In mathematics, in the area of harmonic analysis, the fractional Fourier transform (FRFT) is a family of linear transformations generalizing the Fourier transform. It can be thought of as the Fourier transform to the ''n''-th power, where ''n'' need not be an integer — thus, it can transform a function to any ''intermediate'' domain between time and frequency. Its applications range from filter design and signal analysis to phase retrieval and pattern recognition. The FRFT can be used to define fractional convolution, correlation, and other operations, and can also be further generalized into the linear canonical transformation (LCT). An early definition of the FRFT was introduced by Condon, by solving for the Green's function for phase-space rotations, and also by Namias, generalizing work of Wiener on Hermite polynomials. However, it was not widely recognized in signal processing until it was independently reintroduced around 1993 by several groups. Since then, there h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Canonical Transformation
In Hamiltonian mechanics, the linear canonical transformation (LCT) is a family of integral transforms that generalizes many classical transforms. It has 4 parameters and 1 constraint, so it is a 3-dimensional family, and can be visualized as the action of the special linear group SL2(R) on the time–frequency plane (domain). As this defines the original function up to a sign, this translates into an action of its double cover on the original function space. The LCT generalizes the Fourier, fractional Fourier, Laplace, Gauss–Weierstrass, Bargmann and the Fresnel transforms as particular cases. The name "linear canonical transformation" is from canonical transformation, a map that preserves the symplectic structure, as SL2(R) can also be interpreted as the symplectic group Sp2, and thus LCTs are the linear maps of the time–frequency domain which preserve the symplectic form, and their action on the Hilbert space is given by the Metaplectic group. The basic properties of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mirror
A mirror or looking glass is an object that Reflection (physics), reflects an image. Light that bounces off a mirror will show an image of whatever is in front of it, when focused through the lens of the eye or a camera. Mirrors reverse the direction of the image in an equal yet opposite angle from which the light shines upon it. This allows the viewer to see themselves or objects behind them, or even objects that are at an angle from them but out of their field of view, such as around a corner. Natural mirrors have existed since prehistoric times, such as the surface of water, but people have been manufacturing mirrors out of a variety of materials for thousands of years, like stone, metals, and glass. In modern mirrors, metals like silver or aluminium are often used due to their high reflectivity, applied as a thin coating on glass because of its naturally smooth and very Hardness (materials science), hard surface. A mirror is a Wave (physics), wave reflector. Light consis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |