reflectivity on:
[Wikipedia]
[Google]
[Amazon]
 The reflectance of the surface of a
The reflectance of the surface of a
 For homogeneous and semi-infinite (see halfspace) materials, reflectivity is the same as reflectance.
Reflectivity is the square of the magnitude of the Fresnel reflection coefficient,E. Hecht (2001). Optics (4th ed.). Pearson Education. .
which is the ratio of the reflected to incident electric field;
as such the reflection coefficient can be expressed as a
For homogeneous and semi-infinite (see halfspace) materials, reflectivity is the same as reflectance.
Reflectivity is the square of the magnitude of the Fresnel reflection coefficient,E. Hecht (2001). Optics (4th ed.). Pearson Education. .
which is the ratio of the reflected to incident electric field;
as such the reflection coefficient can be expressed as a
/ref>
Light Reflection from Water Waves: Suitable Setup for a Polarimetric Investigation under Controlled Laboratory Conditions
'. Journal of Atmospheric and Oceanic Technology, 25 (5), 715--728. Fresnel reflection is directional and therefore does not contribute significantly to albedo which primarily diffuses reflection. A real water surface may be wavy. Reflectance, which assumes a flat surface as given by the Fresnel equations, can be adjusted to account for waviness.
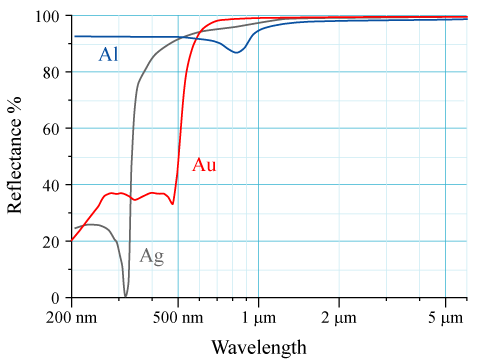
Reflectivity of metals (chart)
{{Webarchive, url=https://web.archive.org/web/20160304024228/http://www.tvu.com/metalreflectivityLR.jpg , date=2016-03-04 .
Physical quantities Radiometry Dimensionless numbers
 The reflectance of the surface of a
The reflectance of the surface of a material
Material is a substance or mixture of substances that constitutes an object. Materials can be pure or impure, living or non-living matter. Materials can be classified on the basis of their physical and chemical properties, or on their geolo ...
is its effectiveness in reflecting radiant energy. It is the fraction of incident electromagnetic power that is reflected at the boundary. Reflectance is a component of the response of the electronic structure of the material to the electromagnetic field of light, and is in general a function of the frequency, or wavelength, of the light, its polarization, and the angle of incidence
Angle of incidence is a measure of deviation of something from "straight on" and may refer to:
* Angle of incidence (aerodynamics), angle between a wing chord and the longitudinal axis, as distinct from angle of attack
In fluid dynamics, ang ...
. The dependence of reflectance on the wavelength is called a ''reflectance spectrum'' or ''spectral reflectance curve''.
Mathematical definitions
Hemispherical reflectance
The ''hemispherical reflectance'' of a surface, denoted , is defined as where is theradiant flux
In radiometry, radiant flux or radiant power is the radiant energy emitted, reflected, transmitted, or received per unit time, and spectral flux or spectral power is the radiant flux per unit frequency or wavelength, depending on whether the Spec ...
''reflected'' by that surface and is the radiant flux ''received'' by that surface.
Spectral hemispherical reflectance
The ''spectral hemispherical reflectance in frequency'' and ''spectral hemispherical reflectance in wavelength'' of a surface, denoted and respectively, are defined as where * is the spectral radiant flux in frequency ''reflected'' by that surface; * is the spectral radiant flux in frequency received by that surface; * is the spectral radiant flux in wavelength ''reflected'' by that surface; * is the spectral radiant flux in wavelength received by that surface.Directional reflectance
The ''directional reflectance'' of a surface, denoted ''R''Ω, is defined as where * is the radiance ''reflected'' by that surface; * is the radiance received by that surface. This depends on both the reflected direction and the incoming direction. In other words, it has a value for every combination of incoming and outgoing directions. It is related to the bidirectional reflectance distribution function and its upper limit is 1. Another measure of reflectance, depending only on the outgoing direction, is ''I''/''F'', where ''I'' is the radiance reflected in a given direction and ''F'' is the incoming radiance averaged over all directions, in other words, the total flux of radiation hitting the surface per unit area, divided by π. This can be greater than 1 for a glossy surface illuminated by a source such as the sun, with the reflectance measured in the direction of maximum radiance (see also Seeliger effect).Spectral directional reflectance
The ''spectral directional reflectance in frequency'' and ''spectral directional reflectance in wavelength'' of a surface, denoted and respectively, are defined as where * is the spectral radiance in frequency ''reflected'' by that surface; * is the spectral radiance received by that surface; * is the spectral radiance in wavelength ''reflected'' by that surface; * is the spectral radiance in wavelength received by that surface. Again, one can also define a value of (see above) for a given wavelength.Reflectivity
complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
as determined by the Fresnel equations for a single layer, whereas the reflectance is always a positive real number
In mathematics, a real number is a number that can be used to measurement, measure a ''continuous'' one-dimensional quantity such as a distance, time, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small var ...
.
For layered and finite media, according to the CIE, reflectivity is distinguished from ''reflectance'' by the fact that reflectivity is a value that applies to ''thick'' reflecting objects. When reflection occurs from thin layers of material, internal reflection effects can cause the reflectance to vary with surface thickness. Reflectivity is the limit value of reflectance as the sample becomes thick; it is the intrinsic reflectance of the surface, hence irrespective of other parameters such as the reflectance of the rear surface. Another way to interpret this is that the reflectance is the fraction of electromagnetic power reflected from a specific sample, while reflectivity is a property of the material itself, which would be measured on a perfect machine if the material filled half of all space.Palmer and Grant, ''The Art of Radiometry''/ref>
Surface type
Given that reflectance is a directional property, most surfaces can be divided into those that give specular reflection and those that give diffuse reflection. For specular surfaces, such as glass or polished metal, reflectance is nearly zero at all angles except at the appropriate reflected angle; that is the same angle with respect to the surface normal in the plane of incidence, but on the opposing side. When the radiation is incident normal to the surface, it is reflected back into the same direction. For diffuse surfaces, such as matte white paint, reflectance is uniform; radiation is reflected in all angles equally or near-equally. Such surfaces are said to be Lambertian. Most practical objects exhibit a combination of diffuse and specular reflective properties.Water reflectance
Reflection occurs when light moves from a medium with oneindex of refraction
In optics, the refractive index (or refraction index) of an optical medium is a dimensionless number that gives the indication of the light bending ability of that medium.
The refractive index determines how much the path of light is bent, or ...
into a second medium with a different index of refraction.
Specular reflection from a body of water is calculated by the Fresnel equations.Ottaviani, M. and Stamnes, K. and Koskulics, J. and Eide, H. and Long, S.R. and Su, W. and Wiscombe, W., 2008:Light Reflection from Water Waves: Suitable Setup for a Polarimetric Investigation under Controlled Laboratory Conditions
'. Journal of Atmospheric and Oceanic Technology, 25 (5), 715--728. Fresnel reflection is directional and therefore does not contribute significantly to albedo which primarily diffuses reflection. A real water surface may be wavy. Reflectance, which assumes a flat surface as given by the Fresnel equations, can be adjusted to account for waviness.
Grating efficiency
The generalization of reflectance to a diffraction grating, which disperses light by wavelength, is called '' diffraction efficiency''.Other radiometric coefficients
See also
* Bidirectional reflectance distribution function * Colorimetry * Emissivity * Lambert's cosine law * Transmittance * Sun path * Light Reflectance Value * AlbedoReferences
External links
Reflectivity of metals (chart)
{{Webarchive, url=https://web.archive.org/web/20160304024228/http://www.tvu.com/metalreflectivityLR.jpg , date=2016-03-04 .
Physical quantities Radiometry Dimensionless numbers