|
A-stability
In mathematics, a stiff equation is a differential equation for which certain numerical methods for solving the equation are numerically unstable, unless the step size is taken to be extremely small. It has proven difficult to formulate a precise definition of stiffness, but the main idea is that the equation includes some terms that can lead to rapid variation in the solution. When integrating a differential equation numerically, one would expect the requisite step size to be relatively small in a region where the solution curve displays much variation and to be relatively large where the solution curve straightens out to approach a line with slope nearly zero. For some problems this is not the case. In order for a numerical method to give a reliable solution to the differential system sometimes the step size is required to be at an unacceptably small level in a region where the solution curve is very smooth. The phenomenon is known as ''stiffness''. In some cases there may be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Multistep Method
Linear multistep methods are used for the numerical solution of ordinary differential equations. Conceptually, a numerical method starts from an initial point and then takes a short step forward in time to find the next solution point. The process continues with subsequent steps to map out the solution. Single-step methods (such as Euler's method) refer to only one previous point and its derivative to determine the current value. Methods such as Runge–Kutta take some intermediate steps (for example, a half-step) to obtain a higher order method, but then discard all previous information before taking a second step. Multistep methods attempt to gain efficiency by keeping and using the information from previous steps rather than discarding it. Consequently, multistep methods refer to several previous points and derivative values. In the case of ''linear'' multistep methods, a linear combination of the previous points and derivative values is used. Definitions Numerical method ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
L-stability
Within mathematics regarding differential equations, L-stability is a special case of A-stability, a property of Runge–Kutta methods for solving ordinary differential equations. A method is L-stable if it is A-stable and \phi(z) \to 0 as z \to \infty , where \phi is the stability function of the method (the stability function of a Runge–Kutta method is a rational function and thus the limit as z \to +\infty is the same as the limit as z \to -\infty). L-stable methods are in general very good at integrating stiff equation In mathematics, a stiff equation is a differential equation for which certain numerical methods for solving the equation are numerically unstable, unless the step size is taken to be extremely small. It has proven difficult to formulate a precise ...s. References * . Numerical differential equations {{mathapplied-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Ordinary Differential Equations
Numerical methods for ordinary differential equations are methods used to find numerical approximations to the solutions of ordinary differential equations (ODEs). Their use is also known as "numerical integration", although this term can also refer to the computation of integrals. Many differential equations cannot be solved exactly. For practical purposes, however – such as in engineering – a numeric approximation to the solution is often sufficient. The algorithms studied here can be used to compute such an approximation. An alternative method is to use techniques from calculus to obtain a series expansion of the solution. Ordinary differential equations occur in many scientific disciplines, including physics, chemistry, biology, and economics. In addition, some methods in numerical partial differential equations convert the partial differential equation into an ordinary differential equation, which must then be solved. The problem A first-order differenti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Numerical Stability
In the mathematical subfield of numerical analysis, numerical stability is a generally desirable property of numerical algorithms. The precise definition of stability depends on the context. One is numerical linear algebra and the other is algorithms for solving ordinary and partial differential equations by discrete approximation. In numerical linear algebra, the principal concern is instabilities caused by proximity to singularities of various kinds, such as very small or nearly colliding eigenvalues. On the other hand, in numerical algorithms for differential equations the concern is the growth of round-off errors and/or small fluctuations in initial data which might cause a large deviation of final answer from the exact solution. Some numerical algorithms may damp out the small fluctuations (errors) in the input data; others might magnify such errors. Calculations that can be proven not to magnify approximation errors are called ''numerically stable''. One of the common ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Control System
A control system manages, commands, directs, or regulates the behavior of other devices or systems using control loops. It can range from a single home heating controller using a thermostat controlling a domestic boiler to large industrial control systems which are used for controlling processes or machines. The control systems are designed via control engineering process. For continuously modulated control, a feedback controller is used to automatically control a process or operation. The control system compares the value or status of the process variable (PV) being controlled with the desired value or setpoint (SP), and applies the difference as a control signal to bring the process variable output of the plant to the same value as the setpoint. For sequential and combinational logic, software logic, such as in a programmable logic controller, is used. Open-loop and closed-loop control There are two common classes of control action: open loop and closed loop. I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chemical Kinetics
Chemical kinetics, also known as reaction kinetics, is the branch of physical chemistry that is concerned with understanding the rates of chemical reactions. It is to be contrasted with chemical thermodynamics, which deals with the direction in which a reaction occurs but in itself tells nothing about its rate. Chemical kinetics includes investigations of how experimental conditions influence the speed of a chemical reaction and yield information about the reaction's mechanism and transition states, as well as the construction of mathematical models that also can describe the characteristics of a chemical reaction. History In 1864, Peter Waage and Cato Guldberg pioneered the development of chemical kinetics by formulating the law of mass action, which states that the speed of a chemical reaction is proportional to the quantity of the reacting substances.C.M. Guldberg and P. Waage,"Studies Concerning Affinity" ''Forhandlinger i Videnskabs-Selskabet i Christiania'' (1864), 3 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonic Oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its Mechanical equilibrium, equilibrium position, experiences a restoring force ''F'' Proportionality (mathematics), proportional to the displacement ''x'': \vec F = -k \vec x, where ''k'' is a positive coefficient, constant. If ''F'' is the only force acting on the system, the system is called a simple harmonic oscillator, and it undergoes simple harmonic motion: sinusoidal oscillations about the equilibrium point, with a constant amplitude and a constant frequency (which does not depend on the amplitude). If a frictional force (Damping ratio, damping) proportional to the velocity is also present, the harmonic oscillator is described as a damped oscillator. Depending on the friction coefficient, the system can: * Oscillate with a frequency lower than in the Damping ratio, undamped case, and an amplitude decreasing with time (Damping ratio, underdamped oscillator). * Decay to the equilibrium p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
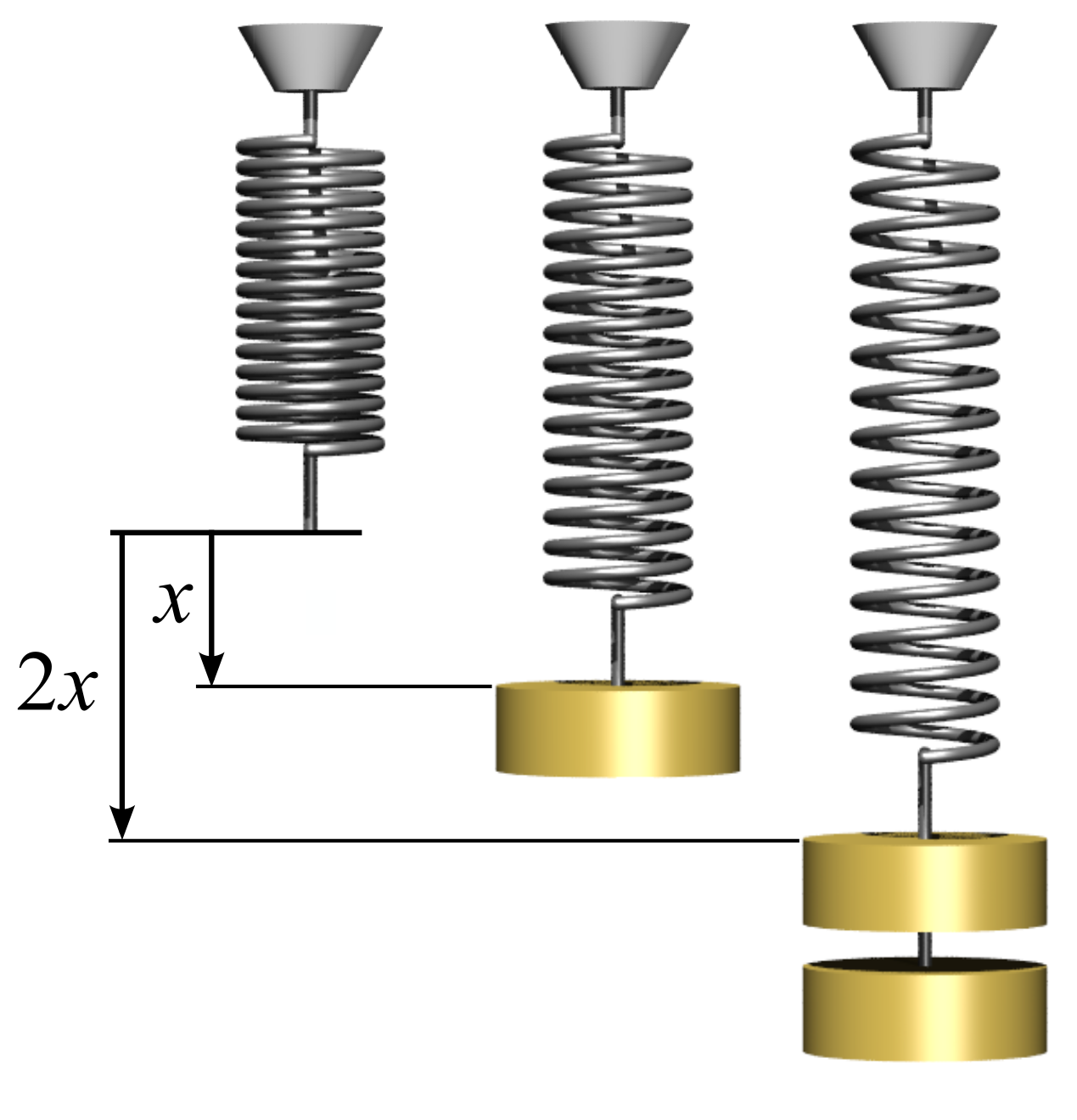
Hooke's Law
In physics, Hooke's law is an empirical law which states that the force () needed to extend or compress a spring by some distance () scales linearly with respect to that distance—that is, where is a constant factor characteristic of the spring (i.e., its stiffness), and is small compared to the total possible deformation of the spring. The law is named after 17th-century British physicist Robert Hooke. He first stated the law in 1676 as a Latin anagram. He published the solution of his anagram in 1678 as: ("as the extension, so the force" or "the extension is proportional to the force"). Hooke states in the 1678 work that he was aware of the law since 1660. Hooke's equation holds (to some extent) in many other situations where an elastic body is deformed, such as wind blowing on a tall building, and a musician plucking a string of a guitar. An elastic body or material for which this equation can be assumed is said to be linear-elastic or Hookean. Hooke's law i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stiffness
Stiffness is the extent to which an object resists deformation in response to an applied force. The complementary concept is flexibility or pliability: the more flexible an object is, the less stiff it is. Calculations The stiffness, k, of a body is a measure of the resistance offered by an elastic body to deformation. For an elastic body with a single degree of freedom (DOF) (for example, stretching or compression of a rod), the stiffness is defined as k = \frac where, * F is the force on the body * \delta is the displacement produced by the force along the same degree of freedom (for instance, the change in length of a stretched spring) In the International System of Units, stiffness is typically measured in newtons per meter (N/m). In Imperial units, stiffness is typically measured in pounds (lbs) per inch. Generally speaking, deflections (or motions) of an infinitesimal element (which is viewed as a point) in an elastic body can occur along multiple DOF (maximum of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stability Region For Euler Method
Stability may refer to: Mathematics *Stability theory, the study of the stability of solutions to differential equations and dynamical systems **Asymptotic stability **Linear stability **Lyapunov stability **Orbital stability **Structural stability *Stability (probability), a property of probability distributions *Stability (learning theory), a property of machine learning algorithms *Stability, a property of sorting algorithms * Numerical stability, a property of numerical algorithms which describes how errors in the input data propagate through the algorithm *Stability radius, a property of continuous polynomial functions *Stable theory, concerned with the notion of stability in model theory *Stability, a property of points in geometric invariant theory *K-Stability, a stability condition for algebraic varieties. *Bridgeland stability conditions, a class of stability conditions on elements of a triangulated category. * Stability (algebraic geometry) Engineering *In atmospheric fl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

.jpg)