|
Ňörńępati
Ňörńępati ( ‚Äď 1066), also transliterated as Shri-pati, was an Indian astronomer, astrologer and mathematician. His major works include ''Dhńękotida-karana'' (1039), a work of twenty verses on solar eclipse, solar and lunar eclipses; ''Dhruva-mńĀnasa'' (written in 1056), a work of 105 verses on calculating planetary longitudes, eclipses and planetary Astronomical transit, transits; ''SiddhńĀnta-Ňõekhara'' a major work on astronomy in 19 chapters; and ''GaŠĻáita-tilaka'', an incomplete arithmetical treatise in 125 verses based on a work by Shridhara. Biography Ňörńępati was born in Rohinikhand in present-day Maharashtra, and lived during (‚Äď1066. His father was Naga-deva (sometimes written as Namadeva) and his grandfather was Kesava. Ňörńępati followed the teachings of Lalla, and wrote on astrology, astronomy and mathematics. He was mainly focused on astrology, and his work on astronomy was aimed at supporting his research on astrology; his work on mathematics, in turn, was aim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lalla
Lalla ( 720‚Äď790 CE) was an Indian Indian mathematics, mathematician, astronomer, and astrologer who belonged to a family of astronomers. Lalla was the son of Trivikrama Bhatta and the grandson of Ňö√Ęmba."Lalla." Complete Dictionary of Scientific Biography. He lived in central India, possibly in the LńĀŠĻ≠a region in modern south Gujarat. Lalla was known as being one of the leading Indian astronomers of the eighth century. Only two of his works are currently thought to be extant.Bracher, Katherine His best-known work is the ''ŇöiŠĻ£yadhńęvŠĻõddhidatantra'' ("Treatise which expands the intellect of students"). This text is one of the first major Sanskrit astronomical texts known from the period following the 7th-century works of Brahmagupta and BhńĀskara I. It generally treats the same astronomical subject matter and demonstrates the same computational techniques as earlier authors, although there are some significant innovations, such that Lalla‚Äôs treatise offers a compromise ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Astronomer
An astronomer is a scientist in the field of astronomy who focuses on a specific question or field outside the scope of Earth. Astronomers observe astronomical objects, such as stars, planets, natural satellite, moons, comets and galaxy, galaxies ‚Äď in either observational astronomy, observational (by analyzing the data) or theoretical astronomy. Examples of topics or fields astronomers study include planetary science, Sun, solar astronomy, the Star formation, origin or stellar evolution, evolution of stars, or the galaxy formation and evolution, formation of galaxies. A related but distinct subject is physical cosmology, which studies the Universe as a whole. Types Astronomers typically fall under either of two main types: observational astronomy, observational and theoretical astronomy, theoretical. Observational astronomers make direct observations of Astronomical object, celestial objects and analyze the data. In contrast, theoretical astronomers create and investigate Con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arithmetic
Arithmetic is an elementary branch of mathematics that deals with numerical operations like addition, subtraction, multiplication, and division. In a wider sense, it also includes exponentiation, extraction of roots, and taking logarithms. Arithmetic systems can be distinguished based on the type of numbers they operate on. Integer arithmetic is about calculations with positive and negative integers. Rational number arithmetic involves operations on fractions of integers. Real number arithmetic is about calculations with real numbers, which include both rational and irrational numbers. Another distinction is based on the numeral system employed to perform calculations. Decimal arithmetic is the most common. It uses the basic numerals from 0 to 9 and their combinations to express numbers. Binary arithmetic, by contrast, is used by most computers and represents numbers as combinations of the basic numerals 0 and 1. Computer arithmetic deals with the specificities of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bikaner State
Bikaner State was the princely state, Princely State in the north-western most part of the History of Bikaner, Rajputana province of imperial British India from 1818 to 1947. The founder of the state Rao Bika was a younger son of Rao Jodha ruler of and founder of the city of Jodhpur State, Jodhpur in Marwar. Rao Bika chose to establish his own kingdom instead of inheriting his father's. Bika defeated the Jat clans of Jangladesh which today refers to the north and north-western Rajasthan along with his uncle Rao Kandhal and his adviser Vikramji Rajpurohit and founded his own kingdom. Its capital was the city of Bikaner. The state was noted for the Bikaner style of painting, Bikaner style of Miniature Painting. Covering a vast area of Bikaner State was the second largest state under the Rajputana Agency after Jodhpur State with a revenue of Rs.26,00,000 in the year 1901. Heeding the 1947 call of Vallabhbhai Patel, Sardar Vallabhbhai Patel to integrate the princely sta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
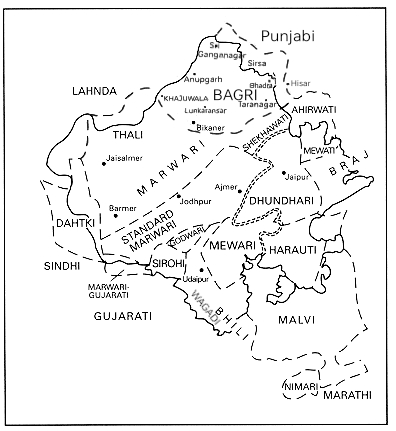
Rajasthani Language
The Rajasthani languages are a group of Western Indo-Aryan languages, primarily spoken in Rajasthan and Malwa, and adjacent areas of Haryana, Gujarat and Madhya Pradesh in India and South Punjab and the adjacent areas of Sindh in Pakistan. They have also reached different corners of India, especially eastern and southern parts of India, due to the migrations of people of the Marwari community who use them for internal communication. Rajasthani languages are also spoken to a lesser extent in Nepal, where they are spoken by 25,394 people according to the 2011 Census of Nepal. The term Rajasthani is also used to refer to a literary language mostly based on Marwari.. Geographical distribution Most of the Rajasthani languages are chiefly spoken in the state of Rajasthan but are also spoken in Gujarat, Western Madhya Pradesh i.e. Malwa and Nimar, Haryana and Punjab. Rajasthani languages are also spoken in the Bahawalpur and Multan sectors of the Pakistani provinces of Punjab an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Marathi Language
Marathi (; , ūĎė¶ūĎė®ūĎėįūĎėôūĎė≤, , ) is a Classical languages of India, classical Indo-Aryan languages, Indo-Aryan language predominantly spoken by Marathi people in the Indian state of Maharashtra and is also spoken in Goa, and parts of Gujarat, Karnataka and the territory of Dadra and Nagar Haveli and Daman and Diu. It is the official language of Maharashtra, and an additional official language in the state of Goa, where it is used for replies, when requests are received in Marathi. It is one of the 22 scheduled languages of India, with 83 million speakers as of 2011. Marathi ranks 13th in the List of languages by number of native speakers, list of languages with most native speakers in the world. Marathi has the List of languages by number of native speakers in India, third largest number of native ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Brahmagupta
Brahmagupta ( ‚Äď ) was an Indian Indian mathematics, mathematician and Indian astronomy, astronomer. He is the author of two early works on mathematics and astronomy: the ''BrńĀhmasphuŠĻ≠asiddhńĀnta'' (BSS, "correctly established Siddhanta, doctrine of Brahma", dated 628), a theoretical treatise, and the ''Khandakhadyaka'' ("edible bite", dated 665), a more practical text. In 628 CE, Brahmagupta first described gravity as an attractive force, and used the term "gurutvńĀkarŠĻ£aŠĻáam (ŗ§óŗ•Āŗ§įŗ•Āŗ§§ŗ•ćŗ§Ķŗ§ĺŗ§ēŗ§įŗ•ćŗ§∑ŗ§£ŗ§ģŗ•ć)" in Sanskrit to describe it. He is also credited with the first clear description of the quadratic formula (the solution of the quadratic equation)Bradley, Michael. ''The Birth of Mathematics: Ancient Times to 1300'', p. 86 (Infobase Publishing 2006) in his main work, the ''BrńĀhma-sphuŠĻ≠a-siddhńĀnta''. Life and career Brahmagupta, according to his own statement, was born in 598 CE. Born in ''BhillamńĀla'' in Gurjaradesa (modern Bhinmal in Rajasthan, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Indeterminate Equation
In mathematics, particularly in number theory, an indeterminate system has fewer equations than unknowns but an additional a set of constraints on the unknowns, such as restrictions that the values be integers. In modern times indeterminate equations are often called Diophantine equations. Examples Linear indeterminate equations An example linear indeterminate equation arises from imagining two equally rich men, one with 5 rubies, 8 sapphires, 7 pearls and 90 gold coins; the other has 7, 9, 6 and 62 gold coins; find the prices (y, c, n) of the respective gems in gold coins. As they are equally rich: 5y + 8c + 7n + 90 = 7y + 9c + 6n + 62 BhńĀskara II gave an general approach to this kind of problem by assigning a fixed integer to one (or N-2 in general) of the unknowns, e.g. n=1, resulting a series of possible solutions like (y, c, n)=(14, 1, 1), (13, 3, 1). For given integers , and , the general linear indeterminant equation is ax + by = n with unknowns and restricted to in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sphere
A sphere (from Ancient Greek, Greek , ) is a surface (mathematics), surface analogous to the circle, a curve. In solid geometry, a sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three-dimensional space.. That given point is the center (geometry), ''center'' of the sphere, and the distance is the sphere's ''radius''. The earliest known mentions of spheres appear in the work of the Greek mathematics, ancient Greek mathematicians. The sphere is a fundamental surface in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubble (physics), Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is spherical Earth, often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres rolling, roll smoothly in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadratic Equation
In mathematics, a quadratic equation () is an equation that can be rearranged in standard form as ax^2 + bx + c = 0\,, where the variable (mathematics), variable represents an unknown number, and , , and represent known numbers, where . (If and then the equation is linear equation, linear, not quadratic.) The numbers , , and are the ''coefficients'' of the equation and may be distinguished by respectively calling them, the ''quadratic coefficient'', the ''linear coefficient'' and the ''constant coefficient'' or ''free term''. The values of that satisfy the equation are called ''solution (mathematics), solutions'' of the equation, and ''zero of a function, roots'' or ''zero of a function, zeros'' of the quadratic function on its left-hand side. A quadratic equation has at most two solutions. If there is only one solution, one says that it is a double root. If all the coefficients are real numbers, there are either two real solutions, or a single real double root, or two comple ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Division (mathematics)
Division is one of the four basic operations of arithmetic. The other operations are addition, subtraction, and multiplication. What is being divided is called the ''dividend'', which is divided by the ''divisor'', and the result is called the ''quotient''. At an elementary level the division of two natural numbers is, among other Quotition and partition, possible interpretations, the process of calculating the number of times one number is contained within another. For example, if 20 apples are divided evenly between 4 people, everyone receives 5 apples (see picture). However, this number of times or the number contained (divisor) need not be integers. The division with remainder or Euclidean division of two natural numbers provides an integer ''quotient'', which is the number of times the second number is completely contained in the first number, and a ''remainder'', which is the part of the first number that remains, when in the course of computing the quotient, no further ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiplication
Multiplication is one of the four elementary mathematical operations of arithmetic, with the other ones being addition, subtraction, and division (mathematics), division. The result of a multiplication operation is called a ''Product (mathematics), product''. Multiplication is often denoted by the cross symbol, , by the mid-line dot operator, , by juxtaposition, or, in programming languages, by an asterisk, . The multiplication of whole numbers may be thought of as repeated addition; that is, the multiplication of two numbers is equivalent to adding as many copies of one of them, the ''multiplicand'', as the quantity of the other one, the ''multiplier''; both numbers can be referred to as ''factors''. This is to be distinguished from term (arithmetic), ''terms'', which are added. :a\times b = \underbrace_ . Whether the first factor is the multiplier or the multiplicand may be ambiguous or depend upon context. For example, the expression 3 \times 4 , can be phrased as "3 ti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |