|
Āryabhaṭa's Sine Table
' The astronomical treatise Āryabhaṭīya was composed during the fifth century by the Indian mathematician and astronomer Āryabhaṭa (476–550 CE), for the computation of the half-chords of certain set of arcs of a circle. It is not a table in the modern sense of a mathematical table; that is, it is not a set of numbers arranged into rows and columns. Āryabhaṭa's table is also not a set of values of the trigonometric sine function in a conventional sense; it is a table of the first differences of the values of trigonometric sines expressed in arcminutes, and because of this the table is also referred to as ''Āryabhaṭa's table of sine-differences''. Āryabhaṭa's table was the first sine table ever constructed in the history of mathematics. The now lost tables of Hipparchus (c.190 BC – c.120 BC) and Menelaus (c.70–140 CE) and those of Ptolemy (c.AD 90 – c.168) were all tables of chords and not of half-chords. Āryabhaṭa's table remained as the standard s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Āryabhaṭīya
''Aryabhatiya'' (IAST: ') or ''Aryabhatiyam'' ('), a Sanskrit astronomical treatise, is the ''magnum opus'' and only known surviving work of the 5th century Indian mathematician Aryabhata. Philosopher of astronomy Roger Billard estimates that the book was composed around 510 CE based on historical references it mentions. Structure and style Aryabhatiya is written in Sanskrit and divided into four sections; it covers a total of 121 verses describing different moralitus via a mnemonic writing style typical for such works in India (see definitions below): 1. Gitikapada (13 verses): large units of time—kalpa, manvantara, and yuga—which present a cosmology different from earlier texts such as Lagadha's Vedanga Jyotisha (ca. 1st century BCE). There is also a table of ine (jya), given in a single verse. The duration of the planetary revolutions during a mahayuga is given as 4.32 million years. 2. Ganitapada (33 verses): covering mensuration (kṣetra vyāvahāra); arithmetic and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kerala School Of Astronomy And Mathematics
The Kerala school of astronomy and mathematics or the Kerala school was a school of Indian mathematics, mathematics and Indian astronomy, astronomy founded by Madhava of Sangamagrama in Kingdom of Tanur, Tirur, Malappuram district, Malappuram, Kerala, India, which included among its members: Parameshvara, Neelakanta Somayaji, Jyeshtadeva, Achyuta Pisharati, Melpathur Narayana Bhattathiri and Achyuta Panikkar. The school flourished between the 14th and 16th centuries and the original discoveries of the school seems to have ended with Melpathur Narayana Bhattathiri, Narayana Bhattathiri (1559–1632). In attempting to solve astronomical problems, the Kerala school independently discovered a number of important mathematical concepts. Their most important results—series expansion for trigonometric functions—were described in Sanskrit verse in a book by Neelakanta called ''Tantrasangraha'', and again in a commentary on this work, called ''Tantrasangraha-vakhya'', of unknown author ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
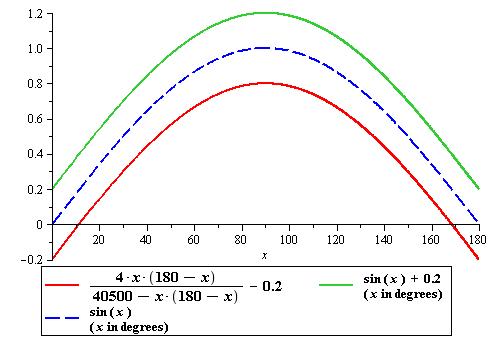
Bhaskara I's Sine Approximation Formula
In mathematics, Bhaskara I's sine approximation formula is a rational expression in one variable for the computation of the approximate values of the trigonometric sines discovered by Bhaskara I (c. 600 – c. 680), a seventh-century Indian mathematician. This formula is given in his treatise titled ''Mahabhaskariya''. It is not known how Bhaskara I arrived at his approximation formula. However, several historians of mathematics have put forward different hypotheses as to the method Bhaskara might have used to arrive at his formula. The formula is elegant, simple and enables one to compute reasonably accurate values of trigonometric sines without using any geometry whatsoever. The approximation formula The formula is given in verses 17 – 19, Chapter VII, Mahabhaskariya of Bhaskara I. A translation of the verses is given below: *(Now) I briefly state the rule (for finding the ''bhujaphala'' and the ''kotiphala'', etc.) without making use of the Rsine-differences 225, e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aryabhatiya
''Aryabhatiya'' (IAST: ') or ''Aryabhatiyam'' ('), a Sanskrit astronomical treatise, is the ''magnum opus'' and only known surviving work of the 5th century Indian mathematician Aryabhata. Philosopher of astronomy Roger Billard estimates that the book was composed around 510 CE based on historical references it mentions. Structure and style Aryabhatiya is written in Sanskrit and divided into four sections; it covers a total of 121 verses describing different moralitus via a mnemonic writing style typical for such works in India (see definitions below): 1. Gitikapada (13 verses): large units of time—kalpa, manvantara, and yuga—which present a cosmology different from earlier texts such as Lagadha's Vedanga Jyotisha (ca. 1st century BCE). There is also a table of ine (jya), given in a single verse. The duration of the planetary revolutions during a mahayuga is given as 4.32 million years. 2. Ganitapada (33 verses): covering mensuration (kṣetra vyāvahāra); arithmetic and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arcseconds
A minute of arc, arcminute (arcmin), arc minute, or minute arc, denoted by the symbol , is a unit of angular measurement equal to of one degree. Since one degree is of a turn (or complete rotation), one minute of arc is of a turn. The nautical mile (nmi) was originally defined as the arc length of a minute of latitude on a spherical Earth, so the actual Earth circumference is very near . A minute of arc is of a radian. A second of arc, arcsecond (arcsec), or arc second, denoted by the symbol , is of an arcminute, of a degree, of a turn, and (about ) of a radian. These units originated in Babylonian astronomy as sexagesimal subdivisions of the degree; they are used in fields that involve very small angles, such as astronomy, optometry, ophthalmology, optics, navigation, land surveying, and marksmanship. To express even smaller angles, standard SI prefixes can be employed; the milliarcsecond (mas) and microarcsecond (μas), for instance, are commonly used in astron ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degree (angle)
A degree (in full, a degree of arc, arc degree, or arcdegree), usually denoted by ° (the degree symbol), is a measurement of a plane (mathematics), plane angle in which one Turn (geometry), full rotation is 360 degrees. It is not an SI unit—the SI unit of angular measure is the radian—but it is mentioned in the SI Brochure, SI brochure as an Non-SI units mentioned in the SI, accepted unit. Because a full rotation equals 2 radians, one degree is equivalent to radians. History The original motivation for choosing the degree as a unit of rotations and angles is unknown. One theory states that it is related to the fact that 360 is approximately the number of days in a year. Ancient astronomers noticed that the sun, which follows through the ecliptic path over the course of the year, seems to advance in its path by approximately one degree each day. Some ancient calendars, such as the Iranian calendar, Persian calendar and the Babylonian calendar, used 360 days for a year. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hindu-Arabic Numerals
Arabic numerals are the ten numerical digits: , , , , , , , , and . They are the most commonly used symbols to write decimal numbers. They are also used for writing numbers in other systems such as octal, and for writing identifiers such as computer symbols, trademarks, or license plates. The term often implies a decimal number, in particular when contrasted with Roman numerals. They are also called Western Arabic numerals, Ghubār numerals, Hindu-Arabic numerals, Western digits, Latin digits, or European digits. The ''Oxford English Dictionary'' differentiates them with the fully capitalized ''Arabic Numerals'' to refer to the Eastern digits. The term numbers or numerals or digits often implies only these symbols, however this can only be inferred from context. It was in the Algerian city of Béjaïa that the Italian scholar Fibonacci first encountered the numerals; his work was crucial in making them known throughout Europe. European trade, books, and colonialism helped p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ISO 15919
ISO 15919 (Transliteration of Devanagari and related Indic scripts into Latin characters) is one of a series of international standards for romanization by the International Organization for Standardization. It was published in 2001 and uses diacritics to map the much larger set of consonants and vowels in Brahmic and Nastaliq scripts to the Latin script. Overview Relation to other systems ISO 15919 is an international standard on the romanization of many Brahmic scripts, which was agreed upon in 2001 by a network of the national standards institutes of 157 countries. However, the Hunterian transliteration system is the "national system of romanization in India" and a United Nations expert group noted about ISO 15919 that "there is no evidence of the use of the system either in India or in international cartographic products." Another standard, United Nations Romanization Systems for Geographical Names (UNRSGN), was developed by the United Nations Group of Experts on Ge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Devanagari
Devanagari ( ; , , Sanskrit pronunciation: ), also called Nagari (),Kathleen Kuiper (2010), The Culture of India, New York: The Rosen Publishing Group, , page 83 is a left-to-right abugida (a type of segmental Writing systems#Segmental systems: alphabets, writing system), based on the ancient Brahmi script, ''Brāhmī'' script, used in the northern Indian subcontinent. It was developed and in regular use by the 7th century CE. The Devanagari script, composed of 47 primary characters, including 14 vowels and 33 consonants, is the fourth most widely List of writing systems by adoption, adopted writing system in the world, being used for over 120 languages.Devanagari (Nagari) , Script Features and Description, SIL International (2013), United States The orthography of this script reflects the pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aryabhata Numeration
Aryabhata (ISO: ) or Aryabhata I (476–550 CE) was an Indian mathematician and astronomer of the classical age of Indian mathematics and Indian astronomy. He flourished in the Gupta Era and produced works such as the '' Aryabhatiya'' (which mentions that in 3600 '' Kali Yuga'', 499 CE, he was 23 years old) and the ''Arya-siddhanta.'' Aryabhata created a system of phonemic number notation in which numbers were represented by consonant-vowel monosyllables. Later commentators such as Brahmagupta divide his work into ''Ganita ("Mathematics"), Kalakriya ("Calculations on Time") and Golapada ("Spherical Astronomy")''. His pure mathematics discusses topics such as determination of square and cube roots, geometrical figures with their properties and mensuration, arithmetric progression problems on the shadow of the gnomon, quadratic equations, linear and indeterminate equations. Aryabhata calculated the value of pi (''π)'' to the fourth decimal digit and was likely aware th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
David Pingree
David Edwin Pingree (January 2, 1933, New Haven, Connecticut – November 11, 2005, Providence, Rhode Island) was an American historian of mathematics in the ancient world. He was a University Professor and Professor of History of Mathematics and Classics at Brown University. Life Pingree graduated from Phillips Academy in Andover, Massachusetts in 1950. He studied at Harvard University, where he earned his doctorate in 1960 with a dissertation on the supposed transmission of Hellenistic astrology to India. His dissertation was supervised by Daniel Henry Holmes Ingalls, Sr. and Otto Eduard Neugebauer. After completing his PhD, Pingree remained at Harvard three more years as a member of its Society of Fellows before moving to the University of Chicago to accept the position of Research Associate at the Oriental Institute. He joined the History of Mathematics Department at Brown University in 1971, eventually holding the chair until his death. As successor to Otto Neugebau ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
