wave equation

The wave equation is a second-order linear partial differential equation for the description of waves or standing wave fields such as mechanical waves (e.g. water waves, sound waves and seismic waves) or electromagnetic waves (including light waves). It arises in fields like acoustics, electromagnetism, and fluid dynamics.

This article focuses on waves in classical physics. Quantum physics uses an operator-based wave equation often as a relativistic wave equation.

Introduction

The wave equation is a hyperbolic partial differential equation describing waves, including traveling and standing waves; the latter can be considered as linear superpositions of waves traveling in opposite directions. This article mostly focuses on the scalar wave equation describing waves in scalars by scalar functions of a time variable (a variable representing time) and one or more spatial variables (variables representing a position in a space under discussion). At the same time, there are vector wave equations describing waves in vectors such as waves for an electrical field, magnetic field, and magnetic vector potential and elastic waves. By comparison with vector wave equations, the scalar wave equation can be seen as a special case of the vector wave equations; in the Cartesian coordinate system, the scalar wave equation is the equation to be satisfied by each component (for each coordinate axis, such as the ''x'' component for the ''x'' axis) of a vector wave without sources of waves in the considered domain (i.e., space and time). For example, in the Cartesian coordinate system, for $(E_x, E_y, E_z)$ as the representation of an electric vector field wave $\vec$ in the absence of wave sources, each coordinate axis component $E_i$ (''i'' = ''x'', ''y'', ''z'') must satisfy the scalar wave equation. Other scalar wave equation solutions are for physical quantities in scalars such as pressure in a liquid or gas, or the displacement along some specific direction of particles of a vibrating solid away from their resting (equilibrium) positions.

The scalar wave equation is
where
* is a fixed non-negative real coefficient representing the propagation speed of the wave
* is a scalar field representing the displacement or, more generally, the conserved quantity (e.g. pressure or density)
* , and are the three spatial coordinates and being the time coordinate.

The equation states that, at any given point, the second derivative of $u$ with respect to time is proportional to the sum of the second derivatives of $u$ with respect to space, with the constant of proportionality being the square of the speed of the wave.

Using notations from vector calculus, the wave equation can be written compactly as
$u_ = c^2 \Delta u,$
or
$\Box u = 0,$
where the double subscript denotes the second-order partial derivative with respect to time, $\Delta$ is the Laplace operator and $\Box$ the d'Alembert operator, defined as:
$u_ = \frac, \qquad \Delta = \frac + \frac + \frac, \qquad \Box = \frac \frac - \Delta.$

A solution to this (two-way) wave equation can be quite complicated. Still, it can be analyzed as a linear combination of simple solutions that are sinusoidal plane waves with various directions of propagation and wavelengths but all with the same propagation speed . This analysis is possible because the wave equation is linear and homogeneous, so that any multiple of a solution is also a solution, and the sum of any two solutions is again a solution. This property is called the superposition principle in physics.

The wave equation alone does not specify a physical solution; a unique solution is usually obtained by setting a problem with further conditions, such as initial conditions, which prescribe the amplitude and phase of the wave. Another important class of problems occurs in enclosed spaces specified by boundary conditions, for which the solutions represent standing waves, or harmonics, analogous to the harmonics of musical instruments.

Wave equation in one space dimension

The wave equation in one spatial dimension can be written as follows:
$\frac = c^2 \frac.$This equation is typically described as having only one spatial dimension , because the only other independent variable is the time .

Derivation

The wave equation in one space dimension can be derived in a variety of different physical settings. Most famously, it can be derived for the case of a string vibrating in a two-dimensional plane, with each of its elements being pulled in opposite directions by the force of tension.Tipler, Paul and Mosca, Gene.
Physics for Scientists and Engineers, Volume 1: Mechanics, Oscillations and Waves; Thermodynamics
', pp. 470–471 (Macmillan, 2004).

Another physical setting for derivation of the wave equation in one space dimension uses Hooke's law. In the theory of elasticity, Hooke's law is an approximation for certain materials, stating that the amount by which a material body is deformed (the strain) is linearly related to the force causing the deformation (the stress).

Hooke's law

The wave equation in the one-dimensional case can be derived from Hooke's law in the following way: imagine an array of little weights of mass interconnected with massless springs of length . The springs have a spring constant of :
:

Here the dependent variable measures the distance from the equilibrium of the mass situated at , so that essentially measures the magnitude of a disturbance (i.e. strain) that is traveling in an elastic material. The resulting force exerted on the mass at the location is:
\begin
F_\text &= F_ - F_x = k (x + 2h, t) - u(x + h, t)- k (x + h,t) - u(x, t)
\end

By equating the latter equation with

$\begin F_\text &= m \, a(t) = m \, \frac u(x + h, t), \end$

the equation of motion for the weight at the location is obtained:
\frac u(x + h, t) = \frac (x + 2h, t) - u(x + h, t) - u(x + h, t) + u(x, t)
If the array of weights consists of weights spaced evenly over the length of total mass , and the total spring constant of the array , we can write the above equation as

$\frac u(x + h, t) = \frac \frac.$

Taking the limit and assuming smoothness, one gets
$\frac = \frac \frac,$
which is from the definition of a second derivative. is the square of the propagation speed in this particular case.

Stress pulse in a bar

In the case of a stress pulse propagating longitudinally through a bar, the bar acts much like an infinite number of springs in series and can be taken as an extension of the equation derived for Hooke's law. A uniform bar, i.e. of constant cross-section, made from a linear elastic material has a stiffness given by
$K = \frac,$
where is the cross-sectional area, and is the Young's modulus of the material. The wave equation becomes
$\frac = \frac \frac.$

is equal to the volume of the bar, and therefore
$\frac = \frac,$
where is the density of the material. The wave equation reduces to
$\frac = \frac \frac.$

The speed of a stress wave in a bar is therefore $\sqrt$.

General solution

Algebraic approach

For the one-dimensional wave equation a relatively simple general solution may be found. Defining new variables
$\begin \xi &= x - c t, \\ \eta &= x + c t \end$
changes the wave equation into
$\frac(x, t) = 0,$
which leads to the general solution
$u(x, t) = F(\xi) + G(\eta) = F(x - c t) + G(x + c t).$

In other words, the solution is the sum of a right-traveling function and a left-traveling function . "Traveling" means that the shape of these individual arbitrary functions with respect to stays constant, however, the functions are translated left and right with time at the speed . This was derived by Jean le Rond d'Alembert.

Another way to arrive at this result is to factor the wave equation using two first-order differential operators:
\left frac - c\frac\right\left frac + c\frac\rightu = 0.
Then, for our original equation, we can define
$v \equiv \frac + c\frac,$
and find that we must have
$\frac - c\frac = 0.$

This advection equation can be solved by interpreting it as telling us that the directional derivative of in the direction is 0. This means that the value of is constant on characteristic lines of the form , and thus that must depend only on , that is, have the form . Then, to solve the first (inhomogenous) equation relating to , we can note that its homogenous solution must be a function of the form , by logic similar to the above. Guessing a particular solution of the form , we find that

\left frac + c\frac\rightG(x + ct) = H(x + ct).

Expanding out the left side, rearranging terms, then using the change of variables simplifies the equation to

$G'(s) = \frac.$

This means we can find a particular solution of the desired form by integration. Thus, we have again shown that obeys .

For an initial-value problem, the arbitrary functions and can be determined to satisfy initial conditions:
$u(x, 0) = f(x),$$u_t(x, 0) = g(x).$

The result is d'Alembert's formula:
$u(x, t) = \frac + \frac \int_^ g(s) \, ds.$

In the classical sense, if , and , then . However, the waveforms and may also be generalized functions, such as the delta-function. In that case, the solution may be interpreted as an impulse that travels to the right or the left.

The basic wave equation is a linear differential equation, and so it will adhere to the superposition principle. This means that the net displacement caused by two or more waves is the sum of the displacements which would have been caused by each wave individually. In addition, the behavior of a wave can be analyzed by breaking up the wave into components, e.g. the Fourier transform breaks up a wave into sinusoidal components.

Plane-wave eigenmodes

Another way to solve the one-dimensional wave equation is to first analyze its frequency eigenmodes. A so-called eigenmode is a solution that oscillates in time with a well-defined ''constant'' angular frequency , so that the temporal part of the wave function takes the form , and the amplitude is a function of the spatial variable , giving a separation of variables for the wave function:
$u_\omega(x, t) = e^ f(x).$

This produces an ordinary differential equation for the spatial part :
$\frac = \frac \left(e^ f(x)\right) = -\omega^2 e^ f(x) = c^2 \frac \left(e^ f(x)\right).$

Therefore,
$\fracf(x) = -\left(\frac\right)^2 f(x),$
which is precisely an eigenvalue equation for , hence the name eigenmode. Known as the Helmholtz equation, it has the well-known plane-wave solutions
$f(x) = A e^,$
with wave number .

The total wave function for this eigenmode is then the linear combination
$u_\omega(x, t) = e^ \left(A e^ + B e^\right) = A e^ + B e^,$
where complex numbers , depend in general on any initial and boundary conditions of the problem.

Eigenmodes are useful in constructing a full solution to the wave equation, because each of them evolves in time trivially with the phase factor $e^,$ so that a full solution can be decomposed into an eigenmode expansion:
$u(x, t) = \int_^\infty s(\omega) u_\omega(x, t) \, d\omega,$
or in terms of the plane waves,
$\begin u(x, t) &= \int_^\infty s_+(\omega) e^ \, d\omega + \int_^\infty s_-(\omega) e^ \, d\omega \\ &= \int_^\infty s_+(\omega) e^ \, d\omega + \int_^\infty s_-(\omega) e^ \, d\omega \\ &= F(x - ct) + G(x + ct), \end$
which is exactly in the same form as in the algebraic approach. Functions are known as the Fourier component and are determined by initial and boundary conditions. This is a so-called frequency-domain method, alternative to direct time-domain propagations, such as FDTD method, of the wave packet , which is complete for representing waves in absence of time dilations. Completeness of the Fourier expansion for representing waves in the presence of time dilations has been challenged by chirp wave solutions allowing for time variation of . The chirp wave solutions seem particularly implied by very large but previously inexplicable radar residuals in the flyby anomaly and differ from the sinusoidal solutions in being receivable at any distance only at proportionally shifted frequencies and time dilations, corresponding to past chirp states of the source.

Vectorial wave equation in three space dimensions

The vectorial wave equation (from which the scalar wave equation can be directly derived) can be obtained by applying a force equilibrium to an infinitesimal volume element. If the medium has a modulus of elasticity $E$ that is homogeneous (i.e. independent of $\mathbf$) within the volume element, then its stress tensor is given by $\mathbf = E \nabla \mathbf$, for a vectorial elastic deflection $\mathbf(\mathbf, t)$. The local equilibrium of:
# the tension force $\operatorname \mathbf = \nabla\cdot(E \nabla \mathbf) = E \Delta\mathbf$ due to deflection $\mathbf$, and
# the inertial force $\rho \partial^2\mathbf/\partial t^2$ caused by the local acceleration $\partial^2\mathbf / \partial t^2$
can be written as $\rho \frac - E \Delta \mathbf = \mathbf.$

By merging density $\rho$ and elasticity module $E,$ the sound velocity $c = \sqrt$ results (material law). After insertion, follows the well-known governing wave equation for a homogeneous medium: Text was copied from this source, which is available under
Creative Commons Attribution 4.0 International License

$\frac - c^2 \Delta \mathbf = \boldsymbol.$
(Note: Instead of vectorial $\mathbf(\mathbf, t),$ only scalar $u(x, t)$ can be used, i.e. waves are travelling only along the $x$ axis, and the scalar wave equation follows as $\frac - c^2 \frac = 0$.)

The above vectorial partial differential equation of the 2nd order delivers two mutually independent solutions. From the quadratic velocity term $c^2 = (+c)^2 = (-c)^2$ can be seen that there are two waves travelling in opposite directions $+c$ and $-c$ are possible, hence results the designation “two-way wave equation”.
It can be shown for plane longitudinal wave propagation that the synthesis of two one-way wave equations leads to a general two-way wave equation. For $\nabla\mathbf = \mathbf,$ special two-wave equation with the d'Alembert operator results:
$\left(\frac - \mathbf \cdot \nabla\right)\left(\frac + \mathbf \cdot \nabla \right) \mathbf = \left(\frac + (\mathbf \cdot \nabla) \mathbf \cdot \nabla\right) \mathbf = \left(\frac + (\mathbf \cdot \nabla)^2\right) \mathbf = \mathbf.$
For $\nabla \mathbf = \mathbf,$ this simplifies to
$\left(\frac + c^2\Delta\right) \mathbf = \mathbf.$
Therefore, the vectorial 1st-order one-way wave equation with waves travelling in a pre-defined propagation direction $\mathbf$ results as
$\frac - \mathbf \cdot \nabla \mathbf = \mathbf.$

Scalar wave equation in three space dimensions

A solution of the initial-value problem for the wave equation in three space dimensions can be obtained from the corresponding solution for a spherical wave. The result can then be also used to obtain the same solution in two space dimensions.

Spherical waves

To obtain a solution with constant frequencies, apply the Fourier transform
$\Psi(\mathbf, t) = \int_^\infty \Psi(\mathbf, \omega) e^ \, d\omega,$
which transforms the wave equation into an elliptic partial differential equation of the form:
$\left(\nabla^2 + \frac\right) \Psi(\mathbf, \omega) = 0.$

This is the Helmholtz equation and can be solved using separation of variables. In spherical coordinates this leads to a separation of the radial and angular variables, writing the solution as:
$\Psi(\mathbf, \omega) = \sum_ f_(r) Y_(\theta, \phi).$
The angular part of the solution take the form of spherical harmonics and the radial function satisfies:
\left frac + \frac \frac + k^2 - \frac\rightf_l(r) = 0.
independent of $m$, with $k^2=\omega^2 / c^2$. Substituting
$f_(r)=\fracu_(r),$
transforms the equation into
\left frac + \frac \frac + k^2 - \frac\rightu_l(r) = 0,
which is the Bessel equation.

Example

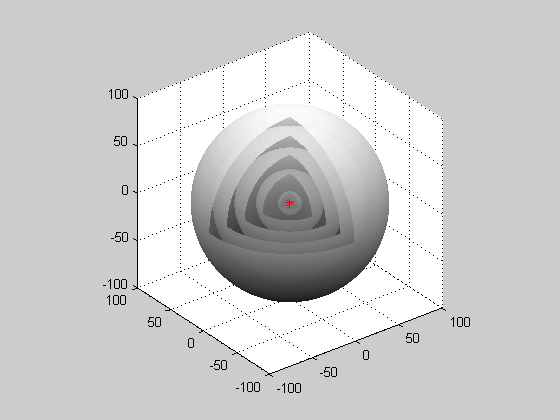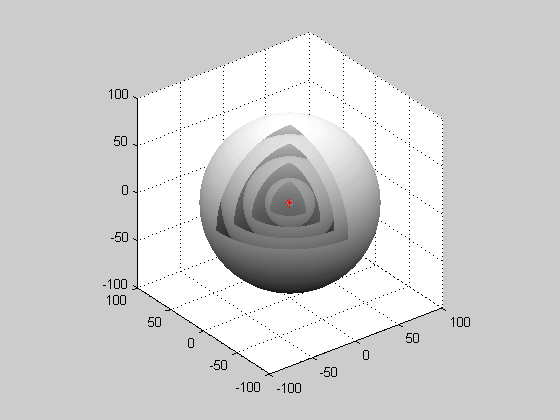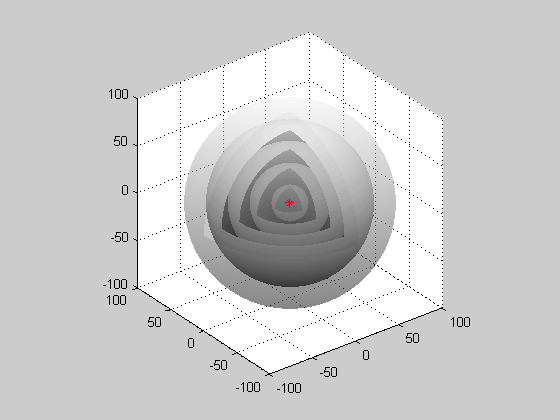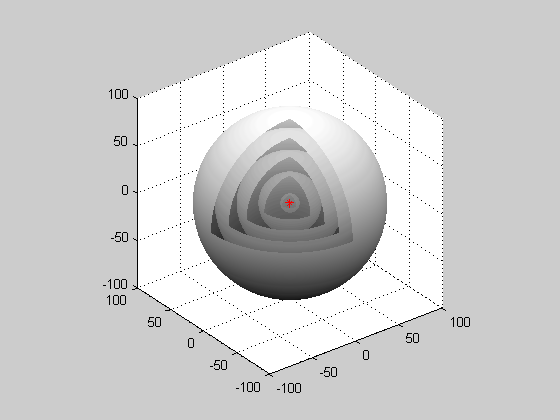
Consider the case . Then there is no angular dependence and the amplitude depends only on the radial distance, i.e., . In this case, the wave equation reduces to$\left(\nabla^2 - \frac \frac\right) \Psi(\mathbf, t) = 0,$
or
$\left(\frac + \frac \frac - \frac \frac\right) u(r, t) = 0.$

This equation can be rewritten as
$\frac - c^2 \frac = 0,$
where the quantity satisfies the one-dimensional wave equation. Therefore, there are solutions in the form$u(r, t) = \frac F(r - ct) + \frac G(r + ct),$
where and are general solutions to the one-dimensional wave equation and can be interpreted as respectively an outgoing and incoming spherical waves. The outgoing wave can be generated by a point source, and they make possible sharp signals whose form is altered only by a decrease in amplitude as increases (see an illustration of a spherical wave on the top right). Such waves exist only in cases of space with odd dimensions.

For physical examples of solutions to the 3D wave equation that possess angular dependence, see dipole radiation.

Monochromatic spherical wave

Although the word "monochromatic" is not exactly accurate, since it refers to light or electromagnetic radiation with well-defined frequency, the spirit is to discover the eigenmode of the wave equation in three dimensions. Following the derivation in the previous section on plane-wave eigenmodes, if we again restrict our solutions to spherical waves that oscillate in time with well-defined ''constant'' angular frequency , then the transformed function has simply plane-wave solutions:$r u(r, t) = Ae^,$
or
$u(r, t) = \frac e^.$

From this we can observe that the peak intensity of the spherical-wave oscillation, characterized as the squared wave amplitude
$I = , u(r, t), ^2 = \frac,$
drops at the rate proportional to , an example of the inverse-square law.

Solution of a general initial-value problem

The wave equation is linear in and is left unaltered by translations in space and time. Therefore, we can generate a great variety of solutions by translating and summing spherical waves. Let be an arbitrary function of three independent variables, and let the spherical wave form be a delta function. Let a family of spherical waves have center at , and let be the radial distance from that point. Thus

$r^2 = (x - \xi)^2 + (y - \eta)^2 + (z - \zeta)^2.$

If is a superposition of such waves with weighting function , then
$u(t, x, y, z) = \frac \iiint \varphi(\xi, \eta, \zeta) \frac \, d\xi \, d\eta \, d\zeta;$
the denominator is a convenience.

From the definition of the delta function, may also be written as
$u(t, x, y, z) = \frac \iint_S \varphi(x + ct\alpha, y + ct\beta, z + ct\gamma) \, d\omega,$
where , , and are coordinates on the unit sphere , and is the area element on . This result has the interpretation that is times the mean value of on a sphere of radius centered at :
u(t, x, y, z) = t M_ varphi

It follows that
$u(0, x, y, z) = 0, \quad u_t(0, x, y, z) = \varphi(x, y, z).$

The mean value is an even function of , and hence if
v(t, x, y, z) = \frac \big(t M_ varphibig),
then
$v(0, x, y, z) = \varphi(x, y, z), \quad v_t(0, x, y, z) = 0.$

These formulas provide the solution for the initial-value problem for the wave equation. They show that the solution at a given point , given depends only on the data on the sphere of radius that is intersected by the light cone drawn backwards from . It does ''not'' depend upon data on the interior of this sphere. Thus the interior of the sphere is a lacuna for the solution. This phenomenon is called Huygens' principle. It is only true for odd numbers of space dimension, where for one dimension the integration is performed over the boundary of an interval with respect to the Dirac measure.

Scalar wave equation in two space dimensions

In two space dimensions, the wave equation is

$u_ = c^2 \left( u_ + u_ \right).$

We can use the three-dimensional theory to solve this problem if we regard as a function in three dimensions that is independent of the third dimension. If

$u(0,x,y)=0, \quad u_t(0,x,y) = \phi(x,y),$

then the three-dimensional solution formula becomes

u(t,x,y) = tM_ phi= \frac \iint_S \phi(x + ct\alpha,\, y + ct\beta) \, d\omega,

where and are the first two coordinates on the unit sphere, and is the area element on the sphere. This integral may be rewritten as a double integral over the disc with center and radius

$u(t,x,y) = \frac \iint_D \frac d\xi \, d\eta.$

It is apparent that the solution at depends not only on the data on the light cone where
$(x -\xi)^2 + (y - \eta)^2 = c^2 t^2 ,$
but also on data that are interior to that cone.

Scalar wave equation in general dimension and Kirchhoff's formulae

We want to find solutions to for with and .

Odd dimensions

Assume is an odd integer, and , for . Let and let

u(x, t)
= \frac \left partial_t \left(\frac \partial_t \right)^ \left(t^ \frac \int_ g \, dS \right) + \left(\frac \partial_t \right)^ \left(t^ \frac \int_ h \, dS \right) \right/math>

Then
* $u \in C^2\big(\mathbf^n \times [0, \infty)\big)$,
* $u_ - \Delta u = 0$ in $\mathbf^n \times (0, \infty)$,
* $\lim_ u(x,t) = g(x^0)$,
* $\lim_ u_t(x,t) = h(x^0)$.

Even dimensions

Assume is an even integer and , , for . Let and let

$u(x,t) = \frac \left [\partial_t \left (\frac \partial_t \right )^ \left (t^n \frac\int_ \frac dy \right ) + \left (\frac \partial_t \right )^ \left (t^n \frac\int_ \frac dy \right ) \right ]$

then
*
* in
*$\lim_ u(x,t) = g(x^0)$
*$\lim_ u_t(x,t) = h(x^0)$

Green's function

Consider the inhomogeneous wave equation in $1+D$ dimensions$(\partial_ - c^2\nabla^2) u = s(t, x)$By rescaling time, we can set wave speed $c = 1$.

Since the wave equation $(\partial_ - \nabla^2) u = s(t, x)$ has order 2 in time, there are two impulse responses: an acceleration impulse and a velocity impulse. The effect of inflicting an acceleration impulse is to suddenly change the wave velocity $\partial_t u$. The effect of inflicting a velocity impulse is to suddenly change the wave displacement $u$.

For acceleration impulse, $s(t,x) = \delta^(t,x)$ where $\delta$ is the Dirac delta function. The solution to this case is called the Green's function $G$ for the wave equation.

For velocity impulse, $s(t, x) = \partial_t \delta^(t,x)$, so if we solve the Green function $G$, the solution for this case is just $\partial_t G$.

Duhamel's principle

The main use of Green's functions is to solve initial value problems by Duhamel's principle, both for the homogeneous and the inhomogeneous case.

Given the Green function $G$, and initial conditions $u(0,x), \partial_t u(0,x)$, the solution to the homogeneous wave equation is$u = (\partial_t G) \ast u + G \ast \partial_t u$where the asterisk is convolution in space. More explicitly, $u(t, x) = \int (\partial_t G)(t, x-x') u(0, x') dx' + \int G(t, x-x') (\partial_t u)(0, x') dx'.$For the inhomogeneous case, the solution has one additional term by convolution over spacetime:$\iint_ G(t-t', x-x') s(t', x')dt' dx'.$

Solution by Fourier transform

By a Fourier transform,$\hat G (\omega)= \frac, \quad G(t, x) = \frac \int \hat G(\omega) e^d\omega_0 d\vec\omega.$The $\omega_0$ term can be integrated by the residue theorem. It would require us to perturb the integral slightly either by $+i\epsilon$ or by $-i\epsilon$, because it is an improper integral. One perturbation gives the forward solution, and the other the backward solution. The forward solution gives$G(t,x) = \frac \int \frac e^d\vec \omega, \quad \partial_t G(t, x) = \frac \int \cos(\, \vec \omega\, t) e^d\vec \omega.$The integral can be solved by analytically continuing the Poisson kernel, giving
G(t, x) = \lim _ \frac
\operatorname\left x\, ^2-(t-i \epsilon)^2\right
where $C_D=\pi^ \Gamma((D+1) / 2)$ is half the surface area of a $(D + 1)$-dimensional hypersphere.

Solutions in particular dimensions

We can relate the Green's function in $D$ dimensions to the Green's function in $D+n$ dimensions.

Lowering dimensions

Given a function $s(t, x)$ and a solution $u(t, x)$ of a differential equation in $(1+D)$ dimensions, we can trivially extend it to $(1+D+n)$ dimensions by setting the additional $n$ dimensions to be constant:
$s(t, x_, x_) = s(t, x_), \quad u(t, x_, x_) = u(t, x_).$Since the Green's function is constructed from $f$ and $u$, the Green's function in $(1+D+n)$ dimensions integrates to the Green's function in $(1+D)$ dimensions:
$G_D(t, x_) = \int_ G_(t, x_, x_) d^n x_.$

Raising dimensions

The Green's function in $D$ dimensions can be related to the Green's function in $D+2$ dimensions. By spherical symmetry,
$G_D(t, r) = \int_ G_(t, \sqrt) dydz.$
Integrating in polar coordinates,
$G_D(t, r) = 2\pi \int_0^\infty G_(t, \sqrt) qdq = 2\pi \int_r^\infty G_(t, q') q'dq',$
where in the last equality we made the change of variables $q' = \sqrt$. Thus, we obtain the recurrence relation$G_(t, r) = -\frac \partial_r G_D(t, r).$

Solutions in ''D = 1, 2, 3''

When $D=1$, the integrand in the Fourier transform is the sinc function$\begin G_1(t, x) &= \frac \int_\R \frac e^d\omega \\ &= \frac \int \operatorname(\omega) e^ d\omega \\ &= \frac \\ &= \begin \frac 12 \theta(t-, x, ) \quad t > 0 \\ -\frac 12 \theta(-t-, x, ) \quad t < 0 \end \end$
where $\sgn$ is the sign function and $\theta$ is the unit step function. One solution is the forward solution, the other is the backward solution.

The dimension can be raised to give the $D=3$ case$G_3(t, r) = \frac$and similarly for the backward solution. This can be integrated down by one dimension to give the $D=2$ case$G_2(t, r) = \int_\R \frac dz = \frac$

Wavefronts and wakes

In $D=1$ case, the Green's function solution is the sum of two wavefronts $\frac + \frac$ moving in opposite directions.

In odd dimensions, the forward solution is nonzero only at $t = r$. As the dimensions increase, the shape of wavefront becomes increasingly complex, involving higher derivatives of the Dirac delta function. For example,$\begin & G_1=\frac \theta(\tau) \\ & G_3=\frac \frac \\ & G_5=\frac\left(\frac+\frac\right) \\ & G_7=\frac\left(3 \frac+3 \frac+\frac\right) \end$where $\tau = t- r$, and the wave speed $c$ is restored.

In even dimensions, the forward solution is nonzero in $r \leq t$, the entire region behind the wavefront becomes nonzero, called a wake. The wake has equation:$G_ (t, x ) = (-1)^ \frac \frac \frac$The wavefront itself also involves increasingly higher derivatives of the Dirac delta function.

This means that a general Huygens' principle – the wave displacement at a point $(t, x)$ in spacetime depends only on the state at points on characteristic rays passing $(t, x)$ – only holds in odd dimensions. A physical interpretation is that signals transmitted by waves remain undistorted in odd dimensions, but distorted in even dimensions.

Hadamard's conjecture states that this generalized Huygens' principle still holds in all odd dimensions even when the coefficients in the wave equation are no longer constant. It is not strictly correct, but it is correct for certain families of coefficients

Problems with boundaries

One space dimension

Reflection and transmission at the boundary of two media

For an incident wave traveling from one medium (where the wave speed is ) to another medium (where the wave speed is ), one part of the wave will transmit into the second medium, while another part reflects back into the other direction and stays in the first medium. The amplitude of the transmitted wave and the reflected wave can be calculated by using the continuity condition at the boundary.

Consider the component of the incident wave with an angular frequency of , which has the waveform
$u^\text(x, t) = Ae^,\quad A \in \C.$
At , the incident reaches the boundary between the two media at . Therefore, the corresponding reflected wave and the transmitted wave will have the waveforms
$u^\text(x, t) = Be^, \quad u^\text(x, t) = Ce^, \quad B, C \in \C.$
The continuity condition at the boundary is
$u^\text(0, t) + u^\text(0, t) = u^\text(0, t), \quad u_x^\text(0, t) + u_x^\text(0, t) = u_x^\text(0, t).$
This gives the equations
$A + B = C, \quad A - B = \frac C = \frac C,$
and we have the reflectivity and transmissivity
$\frac = \frac, \quad \frac = \frac.$
When , the reflected wave has a reflection phase change of 180°, since . The energy conservation can be verified by
$\frac + \frac = \frac.$
The above discussion holds true for any component, regardless of its angular frequency of .

The limiting case of corresponds to a "fixed end" that does not move, whereas the limiting case of corresponds to a "free end".

The Sturm–Liouville formulation

A flexible string that is stretched between two points and satisfies the wave equation for and . On the boundary points, may satisfy a variety of boundary conditions. A general form that is appropriate for applications is

$\begin -u_x(t, 0) + a u(t, 0) &= 0, \\ u_x(t, L) + b u(t, L) &= 0, \end$

where and are non-negative. The case where is required to vanish at an endpoint (i.e. "fixed end") is the limit of this condition when the respective or approaches infinity. The method of separation of variables consists in looking for solutions of this problem in the special form
$u(t, x) = T(t) v(x).$

A consequence is that
$\frac = \frac = -\lambda.$

The eigenvalue must be determined so that there is a non-trivial solution of the boundary-value problem
$\begin v'' + \lambda v = 0,& \\ -v'(0) + a v(0) &= 0, \\ v'(L) + b v(L) &= 0. \end$

This is a special case of the general problem of Sturm–Liouville theory. If and are positive, the eigenvalues are all positive, and the solutions are trigonometric functions. A solution that satisfies square-integrable initial conditions for and can be obtained from expansion of these functions in the appropriate trigonometric series.

Several space dimensions

The one-dimensional initial-boundary value theory may be extended to an arbitrary number of space dimensions. Consider a domain in -dimensional space, with boundary . Then the wave equation is to be satisfied if is in , and . On the boundary of , the solution shall satisfy

$\frac + a u = 0,$

where is the unit outward normal to , and is a non-negative function defined on . The case where vanishes on is a limiting case for approaching infinity. The initial conditions are

$u(0, x) = f(x), \quad u_t(0, x) = g(x),$

where and are defined in . This problem may be solved by expanding and in the eigenfunctions of the Laplacian in , which satisfy the boundary conditions. Thus the eigenfunction satisfies

$\nabla \cdot \nabla v + \lambda v = 0$

in , and

$\frac + a v = 0$

on .

In the case of two space dimensions, the eigenfunctions may be interpreted as the modes of vibration of a drumhead stretched over the boundary . If is a circle, then these eigenfunctions have an angular component that is a trigonometric function of the polar angle , multiplied by a Bessel function (of integer order) of the radial component. Further details are in Helmholtz equation.

If the boundary is a sphere in three space dimensions, the angular components of the eigenfunctions are spherical harmonics, and the radial components are Bessel functions of half-integer order.

Inhomogeneous wave equation in one dimension

The inhomogeneous wave equation in one dimension is
$u_(x, t) - c^2 u_(x, t) = s(x, t)$
with initial conditions
$u(x, 0) = f(x),$
$u_t(x, 0) = g(x).$

The function is often called the source function because in practice it describes the effects of the sources of waves on the medium carrying them. Physical examples of source functions include the force driving a wave on a string, or the charge or current density in the Lorenz gauge of electromagnetism.

One method to solve the initial-value problem (with the initial values as posed above) is to take advantage of a special property of the wave equation in an odd number of space dimensions, namely that its solutions respect causality. That is, for any point , the value of depends only on the values of and and the values of the function between and . This can be seen in d'Alembert's formula, stated above, where these quantities are the only ones that show up in it. Physically, if the maximum propagation speed is , then no part of the wave that cannot propagate to a given point by a given time can affect the amplitude at the same point and time.

In terms of finding a solution, this causality property means that for any given point on the line being considered, the only area that needs to be considered is the area encompassing all the points that could causally affect the point being considered. Denote the area that causally affects point as . Suppose we integrate the inhomogeneous wave equation over this region:
$\iint_ \big(c^2 u_(x, t) - u_(x, t)\big) \, dx \, dt = \iint_ s(x, t) \, dx \, dt.$

To simplify this greatly, we can use Green's theorem to simplify the left side to get the following:
$\int_ \big(c^2 u_x(x, t) \, dt - u_t(x, t) \, dx\big) = \iint_ s(x, t) \, dx \, dt.$

The left side is now the sum of three line integrals along the bounds of the causality region. These turn out to be fairly easy to compute:
$\int^_ -u_t(x, 0) \, dx = -\int^_ g(x) \, dx.$

In the above, the term to be integrated with respect to time disappears because the time interval involved is zero, thus .

For the other two sides of the region, it is worth noting that is a constant, namely , where the sign is chosen appropriately. Using this, we can get the relation , again choosing the right sign:
$\begin \int_ \big(c^2 u_x(x, t) \, dt - u_t(x, t) \, dx\big) &= \int_ \big(c u_x(x, t) \, dx + c u_t(x, t) \, dt \big) \\ &= c \int_ \, du(x, t) \\ &= c u(x_i, t_i) - c f(x_i + c t_i). \end$

And similarly for the final boundary segment:
$\begin \int_ \big(c^2 u_x(x, t) \, dt - u_t(x, t) \, dx\big) &= -\int_ \big(c u_x(x, t) \, dx + c u_t(x, t) \, dt \big) \\ &= -c \int_ \, du(x, t) \\ &= c u(x_i, t_i) - c f(x_i - c t_i). \end$

Adding the three results together and putting them back in the original integral gives
$\begin \iint_ s(x, t) \, dx \, dt &= - \int^_ g(x) \, dx + c u(x_i, t_i) - c f(x_i + c t_i) + c u(x_i,t_i) - c f(x_i - c t_i) \\ &= 2 c u(x_i, t_i) - c f(x_i + c t_i) - c f(x_i - c t_i) - \int^_ g(x) \, dx. \end$

Solving for , we arrive at
$u(x_i, t_i) = \frac + \frac \int^_ g(x) \, dx + \frac \int^_0 \int^_ s(x, t) \, dx \, dt.$

In the last equation of the sequence, the bounds of the integral over the source function have been made explicit. Looking at this solution, which is valid for all choices compatible with the wave equation, it is clear that the first two terms are simply d'Alembert's formula, as stated above as the solution of the homogeneous wave equation in one dimension. The difference is in the third term, the integral over the source.

Further generalizations

Elastic waves

The elastic wave equation (also known as the Navier–Cauchy equation) in three dimensions describes the propagation of waves in an isotropic homogeneous elastic medium. Most solid materials are elastic, so this equation describes such phenomena as seismic waves in the Earth and ultrasonic waves used to detect flaws in materials. While linear, this equation has a more complex form than the equations given above, as it must account for both longitudinal and transverse motion:
$\rho \ddot = \mathbf + (\lambda + 2\mu) \nabla(\nabla \cdot \mathbf) - \mu\nabla \times (\nabla \times \mathbf),$
where:
: and are the so-called Lamé parameters describing the elastic properties of the medium,
: is the density,
: is the source function (driving force),
: is the displacement vector.

By using , the elastic wave equation can be rewritten into the more common form of the Navier–Cauchy equation.

Note that in the elastic wave equation, both force and displacement are vector quantities. Thus, this equation is sometimes known as the vector wave equation.
As an aid to understanding, the reader will observe that if and are set to zero, this becomes (effectively) Maxwell's equation for the propagation of the electric field , which has only transverse waves.

Dispersion relation

In dispersive wave phenomena, the speed of wave propagation varies with the wavelength of the wave, which is reflected by a dispersion relation

$\omega = \omega(\mathbf),$

where is the angular frequency, and is the wavevector describing plane-wave solutions. For light waves, the dispersion relation is , but in general, the constant speed gets replaced by a variable phase velocity:

$v_\text = \frac.$

See also

* Acoustic attenuation
* Acoustic wave equation
* Bateman transform
* Electromagnetic wave equation
*Helmholtz equation
* Inhomogeneous electromagnetic wave equation
*Laplace operator
* Mathematics of oscillation
*Maxwell's equations
*Schrödinger equation
*Standing wave
* Vibrations of a circular membrane
* Wheeler–Feynman absorber theory

Notes

References

* Flint, H.T. (1929) "Wave Mechanics" Methuen & Co. Ltd. London.
*
*
* R. Courant, D. Hilbert, ''Methods of Mathematical Physics, vol II''. Interscience (Wiley) New York, 1962.
*
*
Linear Wave Equations
, ''EqWorld: The World of Mathematical Equations.''
*
Nonlinear Wave Equations
, ''EqWorld: The World of Mathematical Equations.''
* William C. Lane,
MISN-0-201 The Wave Equation and Its Solutions
,
Project PHYSNET
'.

External links

Nonlinear Wave Equations
by Stephen Wolfram and Rob Knapp
Nonlinear Wave Equation Explorer
by Wolfram Demonstrations Project.
* Mathematical aspects of wave equations are discussed on th
Dispersive PDE Wiki
.
* Graham W Griffiths and William E. Schiesser (2009)
Linear and nonlinear wavesScholarpedia
4(7):4308
doi:10.4249/scholarpedia.4308

{{Authority control

Equations of physics
Hyperbolic partial differential equations
Wave mechanics
Functions of space and time