|
Wave Number
In the physical sciences, the wavenumber (or wave number), also known as repetency, is the spatial frequency of a wave. Ordinary wavenumber is defined as the number of wave cycles divided by length; it is a physical quantity with dimension of reciprocal length, expressed in SI units of cycles per metre or reciprocal metre (m−1). Angular wavenumber, defined as the wave phase divided by time, is a quantity with dimension of angle per length and SI units of radians per metre. They are analogous to temporal frequency, respectively the '' ordinary frequency'', defined as the number of wave cycles divided by time (in cycles per second or reciprocal seconds), and the ''angular frequency'', defined as the phase angle divided by time (in radians per second). In multidimensional systems, the wavenumber is the magnitude of the ''wave vector''. The space of wave vectors is called ''reciprocal space''. Wave numbers and wave vectors play an essential role in optics and the physics of w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Commutative Diagram Of Harmonic Wave Properties
In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Perhaps most familiar as a property of arithmetic, e.g. or , the property can also be used in more advanced settings. The name is needed because there are operations, such as division (mathematics), division and subtraction, that do not have it (for example, ); such operations are ''not'' commutative, and so are referred to as noncommutative operations. The idea that simple operations, such as the multiplication (mathematics), multiplication and addition of numbers, are commutative was for many centuries implicitly assumed. Thus, this property was not named until the 19th century, when new algebraic structures started to be studied. Definition A binary operation * on a Set (mathematics), set ''S'' is ''commutative'' if x * y = y * x for all x,y \in S. An operat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Frequency
In physics, angular frequency (symbol ''ω''), also called angular speed and angular rate, is a scalar measure of the angle rate (the angle per unit time) or the temporal rate of change of the phase argument of a sinusoidal waveform or sine function (for example, in oscillations and waves). Angular frequency (or angular speed) is the magnitude of the pseudovector quantity '' angular velocity''. (UP1) Angular frequency can be obtained multiplying '' rotational frequency'', ''ν'' (or ordinary ''frequency'', ''f'') by a full turn (2 radians): . It can also be formulated as , the instantaneous rate of change of the angular displacement, ''θ'', with respect to time, ''t''. (11 pages) Unit In SI[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optical Spectroscopy
Spectroscopy is the field of study that measures and interprets electromagnetic spectra. In narrower contexts, spectroscopy is the precise study of color as generalized from visible light to all bands of the electromagnetic spectrum. Spectroscopy, primarily in the electromagnetic spectrum, is a fundamental exploratory tool in the fields of astronomy, chemistry, materials science, and physics, allowing the composition, physical structure and electronic structure of matter to be investigated at the atomic, molecular and macro scale, and over astronomical distances. Historically, spectroscopy originated as the study of the wavelength dependence of the absorption by gas phase matter of visible light dispersed by a prism. Current applications of spectroscopy include biomedical spectroscopy in the areas of tissue analysis and medical imaging. Matter waves and acoustic waves can also be considered forms of radiative energy, and recently gravitational waves have been associated ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Momentum Operator
In quantum mechanics, the momentum operator is the operator associated with the linear momentum. The momentum operator is, in the position representation, an example of a differential operator. For the case of one particle in one spatial dimension, the definition is: \hat = - i \hbar \frac where is the reduced Planck constant, the imaginary unit, is the spatial coordinate, and a partial derivative (denoted by \partial/\partial x) is used instead of a total derivative () since the wave function is also a function of time. The "hat" indicates an operator. The "application" of the operator on a differentiable wave function is as follows: \hat\psi = - i \hbar \frac In a basis of Hilbert space consisting of momentum eigenstates expressed in the momentum representation, the action of the operator is simply multiplication by , i.e. it is a multiplication operator, just as the position operator is a multiplication operator in the position representation. Note that the definition ab ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reduced Planck Constant
The Planck constant, or Planck's constant, denoted by h, is a fundamental physical constant of foundational importance in quantum mechanics: a photon's energy is equal to its frequency multiplied by the Planck constant, and the wavelength of a matter wave equals the Planck constant divided by the associated particle momentum. The constant was postulated by Max Planck in 1900 as a proportionality constant needed to explain experimental black-body radiation. Planck later referred to the constant as the "quantum of action". In 1905, Albert Einstein associated the "quantum" or minimal element of the energy to the electromagnetic wave itself. Max Planck received the 1918 Nobel Prize in Physics "in recognition of the services he rendered to the advancement of Physics by his discovery of energy quanta". In metrology, the Planck constant is used, together with other constants, to define the kilogram, the SI unit of mass. The SI units are defined in such a way that, when the Pla ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanical
Quantum mechanics is the fundamental physical theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science. Quantum mechanics can describe many systems that classical physics cannot. Classical physics can describe many aspects of nature at an ordinary (macroscopic and (optical) microscopic) scale, but is not sufficient for describing them at very small submicroscopic (atomic and subatomic) scales. Classical mechanics can be derived from quantum mechanics as an approximation that is valid at ordinary scales. Quantum systems have bound states that are quantized to discrete values of energy, momentum, angular momentum, and other quantities, in contrast to classical systems where these quantities can be measured co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elementary Particle
In particle physics, an elementary particle or fundamental particle is a subatomic particle that is not composed of other particles. The Standard Model presently recognizes seventeen distinct particles—twelve fermions and five bosons. As a consequence of flavor and color combinations and antimatter, the fermions and bosons are known to have 48 and 13 variations, respectively. Among the 61 elementary particles embraced by the Standard Model number: electrons and other leptons, quarks, and the fundamental bosons. Subatomic particles such as protons or neutrons, which contain two or more elementary particles, are known as composite particles. Ordinary matter is composed of atoms, themselves once thought to be indivisible elementary particles. The name ''atom'' comes from the Ancient Greek word ''ἄτομος'' ( atomos) which means ''indivisible'' or ''uncuttable''. Despite the theories about atoms that had existed for thousands of years, the factual existence of ato ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electron Diffraction
Electron diffraction is a generic term for phenomena associated with changes in the direction of electron beams due to elastic interactions with atoms. It occurs due to elastic scattering, when there is no change in the energy of the electrons. The negatively charged electrons are scattered due to Coulomb forces when they interact with both the positively charged atomic core and the negatively charged electrons around the atoms. The resulting map of the directions of the electrons far from the sample is called a diffraction pattern, see for instance Figure 1. Beyond patterns showing the directions of electrons, electron diffraction also plays a major role in the contrast of images in electron microscopes. This article provides an overview of electron diffraction and electron diffraction patterns, collective referred to by the generic name electron diffraction. This includes aspects of how in a general way electrons can act as waves, and diffract and interact with matter. It a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Neutron Diffraction
Neutron diffraction or elastic neutron scattering is the application of neutron scattering to the determination of the atomic and/or magnetic structure of a material. A sample to be examined is placed in a beam of Neutron temperature, thermal or cold neutron radiation, neutrons to obtain a diffraction pattern that provides information of the structure of the material. The technique is similar to X-ray diffraction but due to their different scattering properties, neutrons and X-rays provide complementary information: X-Rays are suited for superficial analysis, strong x-rays from synchrotron radiation are suited for shallow depths or thin specimens, while neutrons having high penetration depth are suited for bulk samples.Measurement of residual stress in materials using neutrons IAEA, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
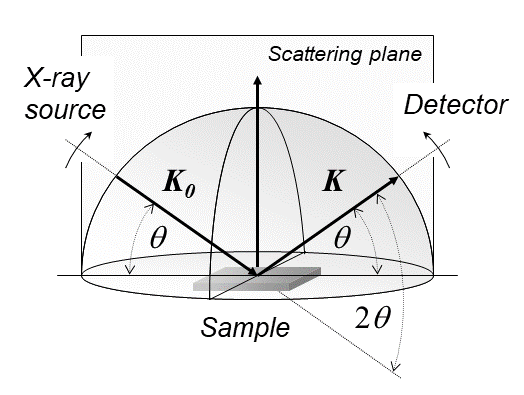
X-ray Diffraction
X-ray diffraction is a generic term for phenomena associated with changes in the direction of X-ray beams due to interactions with the electrons around atoms. It occurs due to elastic scattering, when there is no change in the energy of the waves. The resulting map of the directions of the X-rays far from the sample is called a diffraction pattern. It is different from X-ray crystallography which exploits X-ray diffraction to determine the arrangement of atoms in materials, and also has other components such as ways to map from experimental diffraction measurements to the positions of atoms. This article provides an overview of X-ray diffraction, starting with the early #History, history of x-rays and the discovery that they have the right spacings to be diffracted by crystals. In many cases these diffraction patterns can be #Introduction to x-ray diffraction theory, Interpreted using a single scattering or kinematical theory with conservation of energy (#Ewald's sphere, wave vecto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scattering
In physics, scattering is a wide range of physical processes where moving particles or radiation of some form, such as light or sound, are forced to deviate from a straight trajectory by localized non-uniformities (including particles and radiation) in the medium through which they pass. In conventional use, this also includes deviation of reflected radiation from the angle predicted by the law of reflection. Reflections of radiation that undergo scattering are often called ''diffuse reflections'' and unscattered reflections are called ''specular'' (mirror-like) reflections. Originally, the term was confined to light scattering (going back at least as far as Isaac Newton in the 17th century). As more "ray"-like phenomena were discovered, the idea of scattering was extended to them, so that William Herschel could refer to the scattering of "heat rays" (not then recognized as electromagnetic in nature) in 1800. John Tyndall, a pioneer in light scattering research, noted the connecti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of optical instruments, instruments that use or Photodetector, detect it. Optics usually describes the behaviour of visible light, visible, ultraviolet, and infrared light. Light is a type of electromagnetic radiation, and other forms of electromagnetic radiation such as X-rays, microwaves, and radio waves exhibit similar properties. Most optical phenomena can be accounted for by using the Classical electromagnetism, classical electromagnetic description of light, however complete electromagnetic descriptions of light are often difficult to apply in practice. Practical optics is usually done using simplified models. The most common of these, geometric optics, treats light as a collection of Ray (optics), rays that travel in straight lines and bend when they pass through or reflect from surfaces. Physical optics is a more comprehensive mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |