Viterbi Algorithm

The Viterbi algorithm is a dynamic programming algorithm for obtaining the maximum a posteriori probability estimate of the most likely sequence of hidden states—called the Viterbi path—that results in a sequence of observed events. This is done especially in the context of Markov information sources and hidden Markov models (HMM).

The algorithm has found universal application in decoding the convolutional codes used in both CDMA and GSM digital cellular, dial-up modems, satellite, deep-space communications, and 802.11 wireless LANs. It is now also commonly used in speech recognition, speech synthesis, diarization, keyword spotting, computational linguistics, and bioinformatics. For example, in speech-to-text (speech recognition), the acoustic signal is treated as the observed sequence of events, and a string of text is considered to be the "hidden cause" of the acoustic signal. The Viterbi algorithm finds the most likely string of text given the acoustic signal.

History

The Viterbi algorithm is named after Andrew Viterbi, who proposed it in 1967 as a decoding algorithm for convolutional codes over noisy digital communication links. It has, however, a history of multiple invention, with at least seven independent discoveries, including those by Viterbi, Needleman and Wunsch, and Wagner and Fischer. It was introduced to natural language processing as a method of part-of-speech tagging as early as 1987.

''Viterbi path'' and ''Viterbi algorithm'' have become standard terms for the application of dynamic programming algorithms to maximization problems involving probabilities.
For example, in statistical parsing a dynamic programming algorithm can be used to discover the single most likely context-free derivation (parse) of a string, which is commonly called the "Viterbi parse". Another application is in target tracking, where the track is computed that assigns a maximum likelihood to a sequence of observations.

Algorithm

Given a hidden Markov model with a set of hidden states $S$ and a sequence of $T$ observations $o_0, o_1, \dots, o_$, the Viterbi algorithm finds the most likely sequence of states that could have produced those observations. At each time step $t$, the algorithm solves the subproblem where only the observations up to $o_t$ are considered.

Two matrices of size $T \times \left, \$ are constructed:
* $P_$ contains the maximum probability of ending up at state $s$ at observation $t$, out of all possible sequences of states leading up to it.
* $Q_$ tracks the previous state that was used before $s$ in this maximum probability state sequence.

Let $\pi_s$ and $a_$ be the initial and transition probabilities respectively, and let $b_$ be the probability of observing $o$ at state $s$. Then the values of $P$ are given by the recurrence relation
$P_ = \begin \pi_s \cdot b_ & \text t=0, \\ \max_ \left(P_ \cdot a_ \cdot b_ \right) & \text t>0. \end$
The formula for $Q_$ is identical for $t>0$, except that $\max$ is replaced with $\arg\max$, and $Q_ = 0$.
The Viterbi path can be found by selecting the maximum of $P$ at the final timestep, and following $Q$ in reverse.

Pseudocode

function Viterbi(states, init, trans, emit, obs) is
input states: S hidden states
input init: initial probabilities of each state
input trans: S × S transition matrix
input emit: S × O emission matrix
input obs: sequence of T observations

prob ← T × S matrix of zeroes
prev ← empty T × S matrix
for each state s in states do
prob s] = init * emit obs

for t = 1 to T - 1 inclusive do ''// t = 0 has been dealt with already''
for each state s in states do
for each state r in states do
new_prob ← prob - 1r] * trans * emit obs
if new_prob > prob then
prob ← new_prob
prev ← r

path ← empty array of length T
path - 1← the state s with maximum prob - 1s]
for t = T - 2 to 0 inclusive do
path ← prev + 1path + 1

return path
end

The time complexity of the algorithm is $O(T\times\left, \^2)$. If it is known which state transitions have non-zero probability, an improved bound can be found by iterating over only those $r$ which link to $s$ in the inner loop. Then using amortized analysis one can show that the complexity is $O(T\times(\left, \ + \left, \))$, where $E$ is the number of edges in the graph, i.e. the number of non-zero entries in the transition matrix.

Example

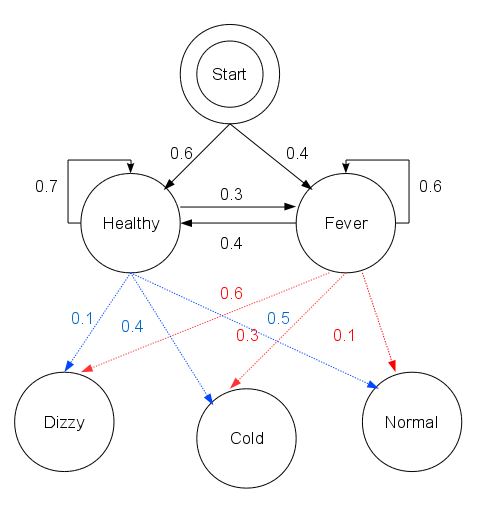
A doctor wishes to determine whether patients are healthy or have a fever. The only information the doctor can obtain is by asking patients how they feel. The patients may report that they either feel normal, dizzy, or cold.

It is believed that the health condition of the patients operates as a discrete Markov chain. There are two states, "healthy" and "fever", but the doctor cannot observe them directly; they are ''hidden'' from the doctor. On each day, the chance that a patient tells the doctor "I feel normal", "I feel cold", or "I feel dizzy", depends only on the patient's health condition on that day.

The ''observations'' (normal, cold, dizzy) along with the ''hidden'' states (healthy, fever) form a hidden Markov model (HMM). From past experience, the probabilities of this model have been estimated as:

init = 
trans = 
emit = 

In this code, init represents the doctor's belief about how likely the patient is to be healthy initially. Note that the particular probability distribution used here is not the equilibrium one, which would be according to the transition probabilities. The transition probabilities trans represent the change of health condition in the underlying Markov chain. In this example, a patient who is healthy today has only a 30% chance of having a fever tomorrow. The emission probabilities emit represent how likely each possible observation (normal, cold, or dizzy) is, given the underlying condition (healthy or fever). A patient who is healthy has a 50% chance of feeling normal; one who has a fever has a 60% chance of feeling dizzy.

A particular patient visits three days in a row, and reports feeling normal on the first day, cold on the second day, and dizzy on the third day.

Firstly, the probabilities of being healthy or having a fever on the first day are calculated. The probability that a patient will be healthy on the first day and report feeling normal is $0.6 \times 0.5 = 0.3$. Similarly, the probability that a patient will have a fever on the first day and report feeling normal is $0.4 \times 0.1 = 0.04$.

The probabilities for each of the following days can be calculated from the previous day directly. For example, the highest chance of being healthy on the second day and reporting to be cold, following reporting being normal on the first day, is the maximum of $0.3 \times 0.7 \times 0.4 = 0.084$ and $0.04 \times 0.4 \times 0.4 = 0.0064$. This suggests it is more likely that the patient was healthy for both of those days, rather than having a fever and recovering.

The rest of the probabilities are summarised in the following table:

From the table, it can be seen that the patient most likely had a fever on the third day. Furthermore, there exists a sequence of states ending on "fever", of which the probability of producing the given observations is 0.01512. This sequence is precisely (healthy, healthy, fever), which can be found be tracing back which states were used when calculating the maxima (which happens to be the best guess from each day but will not always be). In other words, given the observed activities, the patient was most likely to have been healthy on the first day and also on the second day (despite feeling cold that day), and only to have contracted a fever on the third day.

The operation of Viterbi's algorithm can be visualized by means of a trellis diagram. The Viterbi path is essentially the shortest path through this trellis.

Extensions

A generalization of the Viterbi algorithm, termed the ''max-sum algorithm'' (or ''max-product algorithm'') can be used to find the most likely assignment of all or some subset of latent variables in a large number of graphical models, e.g. Bayesian networks, Markov random fields and conditional random fields. The latent variables need, in general, to be connected in a way somewhat similar to a hidden Markov model (HMM), with a limited number of connections between variables and some type of linear structure among the variables. The general algorithm involves ''message passing'' and is substantially similar to the belief propagation algorithm (which is the generalization of the forward-backward algorithm).

With an algorithm called iterative Viterbi decoding, one can find the subsequence of an observation that matches best (on average) to a given hidden Markov model. This algorithm is proposed by Qi Wang et al. to deal with turbo code. Iterative Viterbi decoding works by iteratively invoking a modified Viterbi algorithm, reestimating the score for a filler until convergence.

An alternative algorithm, the Lazy Viterbi algorithm, has been proposed. For many applications of practical interest, under reasonable noise conditions, the lazy decoder (using Lazy Viterbi algorithm) is much faster than the original Viterbi decoder (using Viterbi algorithm). While the original Viterbi algorithm calculates every node in the trellis of possible outcomes, the Lazy Viterbi algorithm maintains a prioritized list of nodes to evaluate in order, and the number of calculations required is typically fewer (and never more) than the ordinary Viterbi algorithm for the same result. However, it is not so easy to parallelize in hardware.

Soft output Viterbi algorithm

The soft output Viterbi algorithm (SOVA) is a variant of the classical Viterbi algorithm.

SOVA differs from the classical Viterbi algorithm in that it uses a modified path metric which takes into account the ''a priori probabilities'' of the input symbols, and produces a ''soft'' output indicating the ''reliability'' of the decision.

The first step in the SOVA is the selection of the survivor path, passing through one unique node at each time instant, ''t''. Since each node has 2 branches converging at it (with one branch being chosen to form the ''Survivor Path'', and the other being discarded), the difference in the branch metrics (or ''cost'') between the chosen and discarded branches indicate the ''amount of error'' in the choice.

This ''cost'' is accumulated over the entire sliding window (usually equals ''at least'' five constraint lengths), to indicate the ''soft output'' measure of reliability of the ''hard bit decision'' of the Viterbi algorithm.

See also

* Expectation–maximization algorithm
* Baum–Welch algorithm
* Forward-backward algorithm
* Forward algorithm
* Error-correcting code
* Viterbi decoder
* Hidden Markov model
* Part-of-speech tagging
* A* search algorithm

References

General references

* (note: the Viterbi decoding algorithm is described in section IV.) Subscription required.
*
* Subscription required.
*
* (Describes the forward algorithm and Viterbi algorithm for HMMs).
* Shinghal, R. and Godfried T. Toussaint, "Experiments in text recognition with the modified Viterbi algorithm," ''IEEE Transactions on Pattern Analysis and Machine Intelligence'', Vol. PAMI-l, April 1979, pp. 184–193.
* Shinghal, R. and Godfried T. Toussaint, "The sensitivity of the modified Viterbi algorithm to the source statistics," ''IEEE Transactions on Pattern Analysis and Machine Intelligence'', vol. PAMI-2, March 1980, pp. 181–185.

External links

* Implementations in Java, F#, Clojure, C# on Wikibooks

Tutorial
on convolutional coding with viterbi decoding, by Chip Fleming

A tutorial for a Hidden Markov Model toolkit (implemented in C) that contains a description of the Viterbi algorithm

Viterbi algorithm
by Dr. Andrew J. Viterbi (scholarpedia.org).

Implementations

Mathematica
has an implementation as part of its support for stochastic processes

Susa
signal processing framework provides the C++ implementation for Forward error correction codes and channel equalizatio
here


C++

C#

Java


Java 8

Julia (HMMBase.jl)

Perl

Prolog
{{Webarchive, url=https://web.archive.org/web/20120502010115/http://www.cs.stonybrook.edu/~pfodor/viterbi/viterbi.P , date=2012-05-02



Go

SFIHMM
includes code for Viterbi decoding.

Eponymous algorithms of mathematics
Error detection and correction
Dynamic programming
Markov models
Articles with example Python (programming language) code