uniform polyhedra

In geometry, a uniform polyhedron has regular polygons as faces and is vertex-transitive—there is an isometry mapping any vertex onto any other. It follows that all vertices are congruent. Uniform polyhedra may be regular (if also face- and edge-transitive), quasi-regular (if also edge-transitive but not face-transitive), or semi-regular (if neither edge- nor face-transitive). The faces and vertices don't need to be convex, so many of the uniform polyhedra are also star polyhedra.

There are two infinite classes of uniform polyhedra, together with 75 other polyhedra. They are 2 infinite classes of prisms and antiprisms, the convex polyhedrons as in 5 Platonic solids and 13 Archimedean solids—2 quasiregular and 11 semiregular— the non-convex star polyhedra as in 4 Kepler–Poinsot polyhedra and 53 uniform star polyhedra—14 quasiregular and 39 semiregular. There are also many degenerate uniform polyhedra with pairs of edges that coincide, including one found by John Skilling called the great disnub dirhombidodecahedron, Skilling's figure.

Dual polyhedra to uniform polyhedra are face-transitive (isohedral) and have regular vertex figures, and are generally classified in parallel with their dual (uniform) polyhedron. The dual of a regular polyhedron is regular, while the dual of an Archimedean solid is a Catalan solid.

The concept of uniform polyhedron is a special case of the concept of uniform polytope, which also applies to shapes in higher-dimensional (or lower-dimensional) space.

Definition

define uniform polyhedra to be vertex-transitive polyhedra with regular faces. They define a polyhedron to be a finite set of polygons such that each side of a polygon is a side of just one other polygon, such that no non-empty proper subset of the polygons has the same property. By a polygon they implicitly mean a polygon in 3-dimensional Euclidean space; these are allowed to be non-convex and intersecting each other.

There are some generalizations of the concept of a uniform polyhedron. If the connectedness assumption is dropped, then we get uniform compounds, which can be split as a union of polyhedra, such as the compound of 5 cubes. If we drop the condition that the realization of the polyhedron is non-degenerate, then we get the so-called degenerate uniform polyhedra. These require a more general definition of polyhedra. gave a rather complicated definition of a polyhedron, while
gave a simpler and more general definition of a polyhedron: in their terminology, a polyhedron is a 2-dimensional abstract polytope with a non-degenerate 3-dimensional realization. Here an abstract polytope is a poset of its "faces" satisfying various condition, a realization is a function from its vertices to some space, and the realization is called non-degenerate if any two distinct faces of the abstract polytope have distinct realizations.
Some of the ways they can be degenerate are as follows:
*Hidden faces. Some polyhedra have faces that are hidden, in the sense that no points of their interior can be seen from the outside. These are usually not counted as uniform polyhedra.
*Degenerate compounds. Some polyhedra have multiple edges and their faces are the faces of two or more polyhedra, though these are not compounds in the previous sense since the polyhedra share edges.
*Double covers. Some non-orientable polyhedra have double covers satisfying the definition of a uniform polyhedron. There double covers have doubled faces, edges and vertices. They are usually not counted as uniform polyhedra.
*Double faces. There are several polyhedra with doubled faces produced by Wythoff's construction. Most authors do not allow doubled faces and remove them as part of the construction.
*Double edges. Skilling's figure has the property that it has double edges (as in the degenerate uniform polyhedra) but its faces cannot be written as a union of two uniform polyhedra.

History

Regular convex polyhedra

* The Platonic solids date back to the classical Greeks and were studied by the Pythagoreans, Plato (c. 424 – 348 BC), Theaetetus (c. 417 BC – 369 BC), Timaeus of Locri (c. 420–380 BC), and Euclid (fl. 300 BC). The Etruscans discovered the regular dodecahedron before 500 BC.

Nonregular uniform convex polyhedra

* The cuboctahedron was known by Plato.
* Archimedes (287 BC – 212 BC) discovered all of the 13 Archimedean solids. His original book on the subject was lost, but Pappus of Alexandria (c. 290 – c. 350 AD) mentioned Archimedes listed 13 polyhedra.
* Piero della Francesca (1415 – 1492) rediscovered the five truncations of the Platonic solids—truncated tetrahedron, truncated octahedron, truncated cube, truncated dodecahedron, and truncated icosahedron—and included illustrations and calculations of their metric properties in his book '' De quinque corporibus regularibus''. He also discussed the cuboctahedron in a different book.
* Luca Pacioli plagiarized Francesca's work in ''De divina proportione'' in 1509, adding the rhombicuboctahedron, calling it an ''icosihexahedron'' for its 26 faces, which was drawn by Leonardo da Vinci.
*Johannes Kepler (1571–1630) was the first to publish the complete list of Archimedean solids, in 1619. He also identified the infinite families of uniform prisms and antiprisms.

Regular star polyhedra

* Kepler (1619) discovered two of the regular Kepler–Poinsot polyhedra, the small stellated dodecahedron and great stellated dodecahedron.
* Louis Poinsot (1809) discovered the other two, the great dodecahedron and great icosahedron.
*The set of four was proven complete by Augustin-Louis Cauchy in 1813 and named by Arthur Cayley in 1859.

Other 53 nonregular star polyhedra

* Of the remaining 53, Edmund Hess (1878) discovered 2, Albert Badoureau (1881) discovered 36 more, and Pitsch (1881) independently discovered 18, of which 3 had not previously been discovered. Together these gave 41 polyhedra.
* The geometer H.S.M. Coxeter discovered the remaining twelve in collaboration with J. C. P. Miller (1930–1932) but did not publish. M.S. Longuet-Higgins and H.C. Longuet-Higgins independently discovered eleven of these. Lesavre and Mercier rediscovered five of them in 1947.
* published the list of uniform polyhedra.
* proved their conjecture that the list was complete.
* In 1974, Magnus Wenninger published his book ''Polyhedron models'', which lists all 75 nonprismatic uniform polyhedra, with many previously unpublished names given to them by Norman Johnson.
* independently proved the completeness and showed that if the definition of uniform polyhedron is relaxed to allow edges to coincide then there is just one extra possibility (the great disnub dirhombidodecahedron).
* In 1987, Edmond Bonan drew all the uniform polyhedra and their duals in 3D with a Turbo Pascal program called Polyca. Most of them were shown during the International Stereoscopic Union Congress held in 1993, at the Congress Theatre, Eastbourne, England; and again in 2005 at the Kursaal of Besançon, France.
* In 1993, Zvi Har'El (1949–2008) produced a complete kaleidoscopic construction of the uniform polyhedra and duals with a computer program called Kaleido and summarized it in a paper ''Uniform Solution for Uniform Polyhedra'', counting figures 1-80.
* Also in 1993, R. Mäder ported this Kaleido solution to Mathematica with a slightly different indexing system.
* In 2002 Peter W. Messer discovered a minimal set of closed-form expressions for determining the main combinatorial and metrical quantities of any uniform polyhedron (and its dual) given only its Wythoff symbol.

Uniform star polyhedra

The 57 nonprismatic nonconvex forms, with exception of the great dirhombicosidodecahedron, are compiled by Wythoff constructions within Schwarz triangles.

Convex forms by Wythoff construction

The convex uniform polyhedra can be named by Wythoff construction operations on the regular form.

In more detail the convex uniform polyhedron are given below by their Wythoff construction within each symmetry group.

Within the Wythoff construction, there are repetitions created by lower symmetry forms. The cube is a regular polyhedron, and a square prism. The octahedron is a regular polyhedron, and a triangular antiprism. The octahedron is also a ''rectified tetrahedron''. Many polyhedra are repeated from different construction sources, and are colored differently.

The Wythoff construction applies equally to uniform polyhedra and uniform tilings on the surface of a sphere, so images of both are given. The spherical tilings include the set of hosohedra and dihedra which are degenerate polyhedra.

These symmetry groups are formed from the reflectional point groups in three dimensions, each represented by a fundamental triangle (''p'' ''q'' ''r''), where ''p'' > 1, ''q'' > 1, ''r'' > 1 and .

* Tetrahedral symmetry (3 3 2) – order 24
* Octahedral symmetry (4 3 2) – order 48
* Icosahedral symmetry (5 3 2) – order 120
* Dihedral symmetry (''n'' 2 2), for ''n'' = 3,4,5,... – order 4''n''

The remaining nonreflective forms are constructed by alternation operations applied to the polyhedra with an even number of sides.

Along with the prisms and their dihedral symmetry, the spherical Wythoff construction process adds two ''regular'' classes which become degenerate as polyhedra : the '' dihedra'' and the '' hosohedra'', the first having only two faces, and the second only two vertices. The truncation of the regular ''hosohedra'' creates the prisms.

Below the convex uniform polyhedra are indexed 1–18 for the nonprismatic forms as they are presented in the tables by symmetry form.

For the infinite set of prismatic forms, they are indexed in four families:
# Hosohedra ''H''_2... (only as spherical tilings)
# Dihedra ''D''_2... (only as spherical tilings)
# Prisms ''P''_3... (truncated hosohedra)
# Antiprisms ''A''_3... (snub prisms)

Summary tables

And a sampling of dihedral symmetries:

(The sphere is not cut, only the tiling is cut.) (On a sphere, an edge is the arc of the great circle, the shortest way, between its two vertices. Hence, a digon whose vertices are not polar-opposite is flat: it looks like an edge.)

(3 3 2) T_d tetrahedral symmetry

The tetrahedral symmetry of the sphere generates 5 uniform polyhedra, and a 6th form by a snub operation.

The tetrahedral symmetry is represented by a fundamental triangle with one vertex with two mirrors, and two vertices with three mirrors, represented by the symbol (3 3 2). It can also be represented by the Coxeter group A₂ or ,3 as well as a Coxeter diagram: .

There are 24 triangles, visible in the faces of the tetrakis hexahedron, and in the alternately colored triangles on a sphere:
:

(4 3 2) O_h octahedral symmetry

The octahedral symmetry of the sphere generates 7 uniform polyhedra, and a 7 more by alternation. Six of these forms are repeated from the tetrahedral symmetry table above.

The octahedral symmetry is represented by a fundamental triangle (4 3 2) counting the mirrors at each vertex. It can also be represented by the Coxeter group B₂ or ,3 as well as a Coxeter diagram: .

There are 48 triangles, visible in the faces of the disdyakis dodecahedron, and in the alternately colored triangles on a sphere:
:

(5 3 2) I_h icosahedral symmetry

The icosahedral symmetry of the sphere generates 7 uniform polyhedra, and a 1 more by alternation. Only one is repeated from the tetrahedral and octahedral symmetry table above.

The icosahedral symmetry is represented by a fundamental triangle (5 3 2) counting the mirrors at each vertex. It can also be represented by the Coxeter group G₂ or ,3 as well as a Coxeter diagram: .

There are 120 triangles, visible in the faces of the disdyakis triacontahedron, and in the alternately colored triangles on a sphere:

(p 2 2) Prismatic ,2 I₂(p) family (D_''p''h dihedral symmetry)

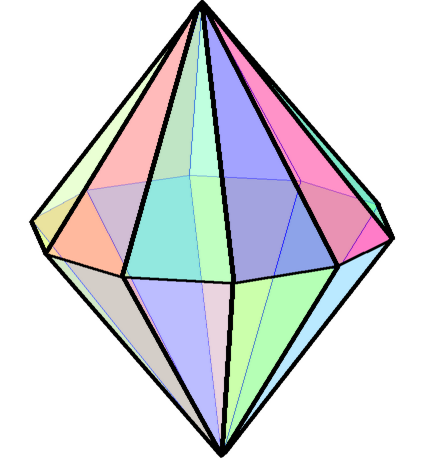
The dihedral symmetry of the sphere generates two infinite sets of uniform polyhedra, prisms and antiprisms, and two more infinite set of degenerate polyhedra, the hosohedra and dihedra which exist as tilings on the sphere.

The dihedral symmetry is represented by a fundamental triangle (p 2 2) counting the mirrors at each vertex. It can also be represented by the Coxeter group I₂(p) or ,2 as well as a prismatic Coxeter diagram: .

Below are the first five dihedral symmetries: D₂ ... D₆. The dihedral symmetry D_p has order ''4n'', represented the faces of a bipyramid, and on the sphere as an equator line on the longitude, and n equally-spaced lines of longitude.

(2 2 2) Dihedral symmetry

There are 8 fundamental triangles, visible in the faces of the square bipyramid (Octahedron) and alternately colored triangles on a sphere:
:

(3 2 2) D_3h dihedral symmetry

There are 12 fundamental triangles, visible in the faces of the hexagonal bipyramid and alternately colored triangles on a sphere:
:

(4 2 2) D_4h dihedral symmetry

There are 16 fundamental triangles, visible in the faces of the octagonal bipyramid and alternately colored triangles on a sphere:
:

(5 2 2) D_5h dihedral symmetry

There are 20 fundamental triangles, visible in the faces of the decagonal bipyramid and alternately colored triangles on a sphere:
:

(6 2 2) D_6h dihedral symmetry

There are 24 fundamental triangles, visible in the faces of the dodecagonal bipyramid and alternately colored triangles on a sphere.

Wythoff construction operators

See also

*Polyhedron
**Regular polyhedron
** Quasiregular polyhedron
** Semiregular polyhedron
* List of uniform polyhedra
** List of uniform polyhedra by vertex figure
** List of uniform polyhedra by Wythoff symbol
** List of uniform polyhedra by Schwarz triangle
* List of Johnson solids
* List of Wenninger polyhedron models
* Polyhedron model
* Uniform tiling
* Uniform tilings in hyperbolic plane
* Pseudo-uniform polyhedron
* List of shapes

Notes

References

* Brückner, M. ''Vielecke und vielflache. Theorie und geschichte.''. Leipzig, Germany: Teubner, 1900

*
*
*
*
*
*
*

External links

*
Uniform Solution for Uniform PolyhedraThe Uniform Polyhedra
Uniform Polyhedra
Uniform polyhedron gallery
''Has a visual chart of all 75''

{{Polytopes

Uniform polyhedra, *