Symmetry breaking on:
[Wikipedia]
[Google]
[Amazon]
 In
In 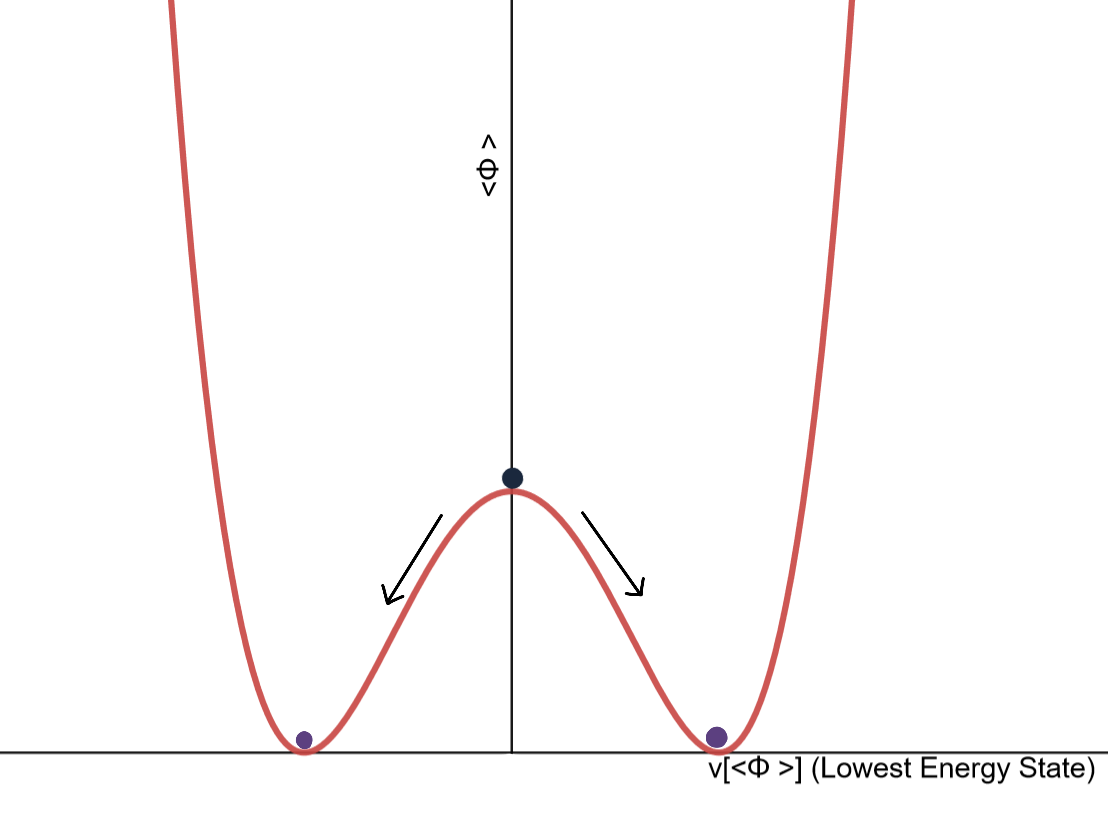 In an infinite system (
In an infinite system (
 In explicit symmetry breaking (ESB), the
In explicit symmetry breaking (ESB), the
physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
, symmetry breaking is a phenomenon where a disordered but symmetric state collapses into an ordered, but less symmetric state. This collapse is often one of many possible bifurcations that a particle can take as it approaches a lower energy state. Due to the many possibilities, an observer may assume the result of the collapse to be arbitrary. This phenomenon is fundamental to quantum field theory
In theoretical physics, quantum field theory (QFT) is a theoretical framework that combines Field theory (physics), field theory and the principle of relativity with ideas behind quantum mechanics. QFT is used in particle physics to construct phy ...
(QFT), and further, contemporary understandings of physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
. Specifically, it plays a central role in the Glashow–Weinberg–Salam model which forms part of the Standard model
The Standard Model of particle physics is the Scientific theory, theory describing three of the four known fundamental forces (electromagnetism, electromagnetic, weak interaction, weak and strong interactions – excluding gravity) in the unive ...
modelling the electroweak sector. In an infinite system (
In an infinite system (Minkowski spacetime
In physics, Minkowski space (or Minkowski spacetime) () is the main mathematical description of spacetime in the absence of gravitation. It combines inertial space and time manifolds into a four-dimensional model.
The model helps show how a s ...
) symmetry breaking occurs, however in a finite system (that is, any real super-condensed system), the system is less predictable, but in many cases quantum tunneling
In physics, a quantum (: quanta) is the minimum amount of any physical entity (physical property) involved in an interaction. The fundamental notion that a property can be "quantized" is referred to as "the hypothesis of quantization". This me ...
occurs. Symmetry breaking and tunneling relate through the collapse of a particle into non-symmetric state as it seeks a lower energy.
Symmetry breaking can be distinguished into two types, explicit
Explicit refers to something that is specific, clear, or detailed. It can also mean:
* Explicit knowledge, knowledge that can be readily articulated, codified and transmitted to others
* Explicit (text), the final words of a text; contrast with inc ...
and spontaneous. They are characterized by whether the equations of motion fail to be invariant, or the ground state
The ground state of a quantum-mechanical system is its stationary state of lowest energy; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state ...
fails to be invariant.
Non-technical description
This section describes spontaneous symmetry breaking. This is the idea that for a physical system, the lowest energy configuration (the vacuum state) is not the most symmetric configuration of the system. Roughly speaking, there are three types of symmetry that can be broken: discrete,continuous
Continuity or continuous may refer to:
Mathematics
* Continuity (mathematics), the opposing concept to discreteness; common examples include
** Continuous probability distribution or random variable in probability and statistics
** Continuous ...
and gauge, ordered in increasing technicality.
An example of a system with discrete symmetry is given by the figure with the red graph: consider a particle moving on this graph, subject to gravity
In physics, gravity (), also known as gravitation or a gravitational interaction, is a fundamental interaction, a mutual attraction between all massive particles. On Earth, gravity takes a slightly different meaning: the observed force b ...
. A similar graph could be given by the function . This system is symmetric under reflection in the y-axis. There are three possible stationary states for the particle: the top of the hill at , or the bottom, at . When the particle is at the top, the configuration respects the reflection symmetry: the particle stays in the same place when reflected. However, the lowest energy configurations are those at . When the particle is in either of these configurations, it is no longer fixed under reflection in the y-axis: reflection swaps the two vacuum states.
An example with continuous symmetry is given by a 3d analogue of the previous example, from rotating the graph around an axis through the top of the hill, or equivalently given by the graph . This is essentially the graph of the Mexican hat potential. This has a continuous symmetry given by rotation about the axis through the top of the hill (as well as a discrete symmetry by reflection through any radial plane). Again, if the particle is at the top of the hill it is fixed under rotations, but it has higher gravitational energy at the top. At the bottom, it is no longer invariant under rotations but minimizes its gravitational potential energy. Furthermore rotations move the particle from one energy minimizing configuration to another. There is a novelty here not seen in the previous example: from any of the vacuum states it is possible to access any other vacuum state with only a small amount of energy, by moving around the trough at the bottom of the hill, whereas in the previous example, to access the other vacuum, the particle would have to cross the hill, requiring a large amount of energy.
Gauge symmetry breaking is the most subtle, but has important physical consequences. Roughly speaking, for the purposes of this section a gauge symmetry is an assignment of systems with continuous symmetry to every point in spacetime
In physics, spacetime, also called the space-time continuum, is a mathematical model that fuses the three dimensions of space and the one dimension of time into a single four-dimensional continuum. Spacetime diagrams are useful in visualiz ...
. Gauge symmetry forbids mass generation for gauge field
In physics, a gauge theory is a type of field theory in which the Lagrangian, and hence the dynamics of the system itself, does not change under local transformations according to certain smooth families of operations (Lie groups). Formally, t ...
s, yet massive gauge fields (W and Z bosons
In particle physics, the W and Z bosons are vector bosons that are together known as the weak bosons or more generally as the intermediate vector bosons. These elementary particles mediate the weak interaction; the respective symbols are , , an ...
) have been observed. Spontaneous symmetry breaking was developed to resolve this inconsistency. The idea is that in an early stage of the universe it was in a high energy state, analogous to the particle being at the top of the hill, and so had full gauge symmetry and all the gauge fields were massless. As it cooled, it settled into a choice of vacuum, thus spontaneously breaking the symmetry, thus removing the gauge symmetry and allowing mass generation of those gauge fields. A full explanation is highly technical: see electroweak interaction
In particle physics, the electroweak interaction or electroweak force is the unified description of two of the fundamental interactions of nature: electromagnetism (electromagnetic interaction) and the weak interaction. Although these two force ...
.
Spontaneous symmetry breaking
Inspontaneous symmetry breaking
Spontaneous symmetry breaking is a spontaneous process of symmetry breaking, by which a physical system in a symmetric state spontaneously ends up in an asymmetric state. In particular, it can describe systems where the equations of motion o ...
(SSB), the equations of motion
In physics, equations of motion are equations that describe the behavior of a physical system in terms of its motion as a function of time. More specifically, the equations of motion describe the behavior of a physical system as a set of mathem ...
of the system are invariant, but any vacuum state (lowest energy state) is not.
For an example with two-fold symmetry, if there is some atom that has two vacuum states, occupying either one of these states breaks the two-fold symmetry. This act of selecting one of the states as the system reaches a lower energy is SSB. When this happens, the atom is no longer symmetric (reflectively symmetric) and has collapsed into a lower energy state.
Such a symmetry breaking is parametrized by an order parameter
In physics, chemistry, and other related fields like biology, a phase transition (or phase change) is the physical process of transition between one state of a medium and another. Commonly the term is used to refer to changes among the basic s ...
. A special case of this type of symmetry breaking is dynamical symmetry breaking
Spontaneous symmetry breaking is a spontaneous process of symmetry breaking
In physics, symmetry breaking is a phenomenon where a disordered but Symmetry in quantum mechanics, symmetric state collapses into an ordered, but less symmetric s ...
.
In the Lagrangian setting of quantum field theory (QFT), the Lagrangian is a functional of quantum fields which is invariant under the action of a symmetry group . However, the vacuum expectation value
In quantum field theory, the vacuum expectation value (VEV) of an operator is its average or expectation value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle. One of the most widely used exa ...
formed when the particle collapses to a lower energy may not be invariant under . In this instance, it will partially break the symmetry of , into a subgroup . This is spontaneous symmetry breaking.
Within the context of gauge symmetry however, SSB is the phenomenon by which gauge fields 'acquire mass' despite gauge-invariance enforcing that such fields be massless. This is because the SSB of gauge symmetry breaks gauge-invariance, and such a break allows for the existence of massive gauge fields. This is an important exemption from Goldstone's theorem
In physics, Goldstone bosons or Nambu–Goldstone bosons (NGBs) are bosons that appear necessarily in models exhibiting spontaneous breakdown of continuous symmetries. They were discovered by Yoichiro Nambu within the context of the BCS superc ...
, where a Nambu-Goldstone boson can gain mass, becoming a Higgs boson
The Higgs boson, sometimes called the Higgs particle, is an elementary particle in the Standard Model of particle physics produced by the excited state, quantum excitation of the Higgs field,
one of the field (physics), fields in particl ...
in the process.
Further, in this context the usage of 'symmetry breaking' while standard, is a misnomer, as gauge 'symmetry' is not really a symmetry but a redundancy in the description of the system. Mathematically, this redundancy is a choice of trivialization, somewhat analogous to redundancy arising from a choice of basis.
Spontaneous symmetry breaking is also associated with phase transitions
In physics, chemistry, and other related fields like biology, a phase transition (or phase change) is the physical process of transition between one state of a medium and another. Commonly the term is used to refer to changes among the basic Sta ...
. For example in the Ising model
The Ising model (or Lenz–Ising model), named after the physicists Ernst Ising and Wilhelm Lenz, is a mathematical models in physics, mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables that r ...
, as the temperature of the system falls below the critical temperature the symmetry of the vacuum is broken, giving a phase transition of the system.
Explicit symmetry breaking
equations of motion
In physics, equations of motion are equations that describe the behavior of a physical system in terms of its motion as a function of time. More specifically, the equations of motion describe the behavior of a physical system as a set of mathem ...
describing a system are variant under the broken symmetry. In Hamiltonian mechanics
In physics, Hamiltonian mechanics is a reformulation of Lagrangian mechanics that emerged in 1833. Introduced by Sir William Rowan Hamilton, Hamiltonian mechanics replaces (generalized) velocities \dot q^i used in Lagrangian mechanics with (gener ...
or Lagrangian mechanics
In physics, Lagrangian mechanics is a formulation of classical mechanics founded on the d'Alembert principle of virtual work. It was introduced by the Italian-French mathematician and astronomer Joseph-Louis Lagrange in his presentation to the ...
, this happens when there is at least one term in the Hamiltonian (or Lagrangian) that explicitly breaks the given symmetry.
In the Hamiltonian setting, this is often studied when the Hamiltonian can be written .
Here is a 'base Hamiltonian', which has some manifest symmetry. More explicitly, it is symmetric under the action of a (Lie) group . Often this is an integrable Hamiltonian.
The is a perturbation or interaction Hamiltonian. This is not invariant under the action of . It is often proportional to a small, perturbative parameter.
This is essentially the paradigm for perturbation theory
In mathematics and applied mathematics, perturbation theory comprises methods for finding an approximate solution to a problem, by starting from the exact solution of a related, simpler problem. A critical feature of the technique is a middle ...
in quantum mechanics. An example of its use is in finding the fine structure
In atomic physics, the fine structure describes the splitting of the spectral lines of atoms due to electron spin and relativistic corrections to the non-relativistic Schrödinger equation. It was first measured precisely for the hydrogen atom ...
of atomic spectra.
Examples
Symmetry breaking can cover any of the following scenarios: :* The breaking of an exact symmetry of the underlying laws of physics by the apparently random formation of some structure; :* A situation in physics in which a minimal energy state has less symmetry than the system itself; :* Situations where the actual state of the system does not reflect the underlying symmetries of the dynamics because the manifestly symmetric state is unstable (stability is gained at the cost oflocal
Local may refer to:
Geography and transportation
* Local (train), a train serving local traffic demand
* Local, Missouri, a community in the United States
Arts, entertainment, and media
* ''Local'' (comics), a limited series comic book by Bria ...
asymmetry);
:* Situations where the equations of a theory may have certain symmetries, though their solutions may not (the symmetries are "hidden").
One of the first cases of broken symmetry discussed in the physics literature is related to the form taken by a uniformly rotating body of incompressible fluid
In fluid mechanics, or more generally continuum mechanics, incompressible flow is a flow in which the material density does not vary over time. Equivalently, the divergence of an incompressible flow velocity is zero. Under certain conditions, t ...
in gravitational and hydrostatic equilibrium
In fluid mechanics, hydrostatic equilibrium, also called hydrostatic balance and hydrostasy, is the condition of a fluid or plastic solid at rest, which occurs when external forces, such as gravity, are balanced by a pressure-gradient force. I ...
. Jacobi and soon later Liouville
Joseph Liouville ( ; ; 24 March 1809 – 8 September 1882) was a French mathematician and engineer.
Life and work
He was born in Saint-Omer in France on 24 March 1809. His parents were Claude-Joseph Liouville (an army officer) and Thérès ...
, in 1834, discussed the fact that a tri-axial ellipsoid was an equilibrium solution for this problem when the kinetic energy compared to the gravitational energy of the rotating body exceeded a certain critical value. The axial symmetry presented by the McLaurin spheroids is broken at this bifurcation point. Furthermore, above this bifurcation point, and for constant angular momentum, the solutions that minimize the kinetic energy are the ''non''-axially symmetric Jacobi ellipsoids instead of the Maclaurin spheroids.
See also
*Higgs mechanism
In the Standard Model of particle physics, the Higgs mechanism is essential to explain the Mass generation, generation mechanism of the property "mass" for gauge bosons. Without the Higgs mechanism, all bosons (one of the two classes of particles ...
* QCD vacuum
* 1964 PRL symmetry breaking papers
References
External links
* {{DEFAULTSORT:Symmetry Breaking Symmetry Pattern formation Theoretical physics Quantum field theory Standard Model