Sterication (geometry) on:
[Wikipedia]
[Google]
[Amazon]
In
 #* There are higher truncations also: bitruncation t1,2 or 2t, tritruncation t2,3 or 3t, quadritruncation t3,4 or 4t, quintitruncation t4,5 or 5t, etc.
# t0,2 or rr: Cantellation - applied to
#* There are higher truncations also: bitruncation t1,2 or 2t, tritruncation t2,3 or 3t, quadritruncation t3,4 or 4t, quintitruncation t4,5 or 5t, etc.
# t0,2 or rr: Cantellation - applied to  #* There are higher cantellations also: bicantellation t1,3 or r2r, tricantellation t2,4 or r3r, quadricantellation t3,5 or r4r, etc.
#* t0,1,2 or tr: Cantitruncation - applied to
#* There are higher cantellations also: bicantellation t1,3 or r2r, tricantellation t2,4 or r3r, quadricantellation t3,5 or r4r, etc.
#* t0,1,2 or tr: Cantitruncation - applied to
 One special operation, called alternation, removes alternate vertices from a polytope with only even-sided faces. An alternated omnitruncated polytope is called a ''snub''.
The resulting polytopes always can be constructed, and are not generally reflective, and also do not in general have ''uniform'' polytope solutions.
The set of polytopes formed by alternating the
One special operation, called alternation, removes alternate vertices from a polytope with only even-sided faces. An alternated omnitruncated polytope is called a ''snub''.
The resulting polytopes always can be constructed, and are not generally reflective, and also do not in general have ''uniform'' polytope solutions.
The set of polytopes formed by alternating the
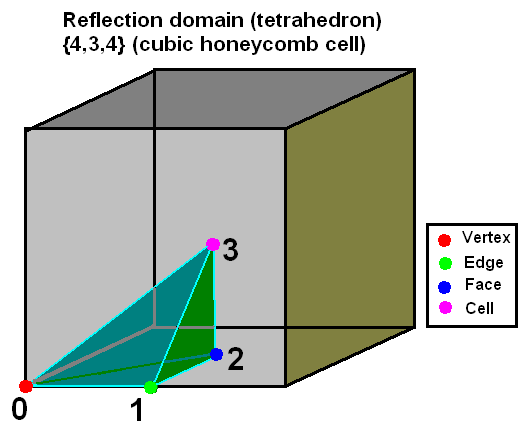
 Every regular polytope can be seen as the images of a fundamental region in a small number of mirrors. In a 4-dimensional polytope (or 3-dimensional cubic honeycomb) the fundamental region is bounded by four mirrors. A mirror in 4-space is a three-dimensional
Every regular polytope can be seen as the images of a fundamental region in a small number of mirrors. In a 4-dimensional polytope (or 3-dimensional cubic honeycomb) the fundamental region is bounded by four mirrors. A mirror in 4-space is a three-dimensional
ONLINE
* A. Boole Stott: ''Geometrical deduction of semiregular from regular polytopes and space fillings'', Verhandelingen of the Koninklijke academy van Wetenschappen width unit Amsterdam, Eerste Sectie 11,1, Amsterdam, 191
PDF
* H.S.M. Coxeter: ** H.S.M. Coxeter, M.S. Longuet-Higgins and J.C.P. Miller: ''Uniform Polyhedra'', Philosophical Transactions of the Royal Society of London, Londne, 195
PDF
** H.S.M. Coxeter, ''Regular Polytopes'', 3rd Edition, Dover New York, 1973 *
', edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ** (Paper 22) H.S.M. Coxeter
Regular and Semi Regular Polytopes I
ath. Zeit. 46 (1940) 380-407, MR 2,10** (Paper 23) H.S.M. Coxeter
Regular and Semi-Regular Polytopes II
ath. Zeit. 188 (1985) 559-591** (Paper 24) H.S.M. Coxeter
Regular and Semi-Regular Polytopes III
ath. Zeit. 200 (1988) 3-45* Marco Möller, ''Vierdimensionale Archimedische Polytope'', Dissertation, Universität Hamburg, Hamburg (2004)
ONLINE
uniform, convex polytopes in four dimensions:
Marco Möller {{Polytopes Uniform polytopes
geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
, a uniform polytope of dimension three or higher is a vertex-transitive
In geometry, a polytope (e.g. a polygon or polyhedron) or a tiling is isogonal or vertex-transitive if all its vertices are equivalent under the symmetries of the figure. This implies that each vertex is surrounded by the same kinds of face i ...
polytope
In elementary geometry, a polytope is a geometric object with flat sides ('' faces''). Polytopes are the generalization of three-dimensional polyhedra to any number of dimensions. Polytopes may exist in any general number of dimensions as an ...
bounded by uniform facets. Here, "vertex-transitive" means that it has symmetries taking every vertex to every other vertex; the same must also be true within each lower-dimensional face of the polytope. In two dimensions (and for two-dimensional faces of higher-dimensional polytopes) a stronger definition is used: only the regular polygon
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either ''convex ...
s are considered as uniform, disallowing polygons that alternate between two different lengths of edges.
This is a generalization of the older category of ''semiregular'' polytopes, but also includes the regular polytope
In mathematics, a regular polytope is a polytope whose symmetry group acts transitive group action, transitively on its flag (geometry), flags, thus giving it the highest degree of symmetry. In particular, all its elements or -faces (for all , w ...
s. Further, star regular faces and vertex figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a general -polytope is sliced off.
Definitions
Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connected ed ...
s (star polygon
In geometry, a star polygon is a type of non-convex polygon. Regular star polygons have been studied in depth; while star polygons in general appear not to have been formally defined, Decagram (geometry)#Related figures, certain notable ones can ...
s) are allowed, which greatly expand the possible solutions. A strict definition requires uniform polytopes to be finite, while a more expansive definition allows uniform honeycombs (2-dimensional tilings and higher dimensional honeycombs) of Euclidean and hyperbolic space
In mathematics, hyperbolic space of dimension ''n'' is the unique simply connected, ''n''-dimensional Riemannian manifold of constant sectional curvature equal to −1.
It is homogeneous, and satisfies the stronger property of being a symme ...
to be considered polytopes as well.
Operations
Nearly every uniform polytope can be generated by aWythoff construction
In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.
Construction process ...
, and represented by a Coxeter diagram
Harold Scott MacDonald "Donald" Coxeter (9 February 1907 – 31 March 2003) was a British-Canadian geometer and mathematician. He is regarded as one of the greatest geometers of the 20th century.
Coxeter was born in England and educated ...
. Notable exceptions include the great dirhombicosidodecahedron in three dimensions and the grand antiprism
In geometry, the grand antiprism or pentagonal double antiprismoid is a uniform 4-polytope (4-dimensional uniform polytope) bounded by 320 cells: 20 pentagonal antiprisms, and 300 tetrahedra. It is an anomalous, non-Wythoffian uniform 4-polyto ...
in four dimensions.
Equivalently, the Wythoffian polytopes can be generated by applying basic operations to the regular polytopes in that dimension. This approach was first used by Johannes Kepler
Johannes Kepler (27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, Natural philosophy, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best know ...
, and is the basis of the Conway polyhedron notation
In geometry and topology, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedra based on a seed polyhedron modified by various prefix operations.
Conway and Hart extended the i ...
.
Rectification operators
Regular n-polytopes have ''n'' orders of rectification. The zeroth rectification is the original form. The (''n''−1)-th rectification is the dual. A rectification reduces edges to vertices, a birectification reduces faces to vertices, a trirectification reduces cells to vertices, a quadirectification reduces 4-faces to vertices, a quintirectification reduced 5-faces to vertices, and so on. An extendedSchläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines List of regular polytopes and compounds, regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, wh ...
can be used for representing rectified forms, with a single subscript:
* ''k''-th rectification = tk = ''k''r.
Truncation operators
Truncation operations that can be applied to regular ''n''-polytopes in any combination. The resulting Coxeter diagram has two ringed nodes, and the operation is named for the distance between them. Truncation cuts vertices, cantellation cuts edges, runcination cuts faces, sterication cut cells. Each higher operation also cuts lower ones too, so a cantellation also truncates vertices. # t0,1 or t: Truncation - applied topolygon
In geometry, a polygon () is a plane figure made up of line segments connected to form a closed polygonal chain.
The segments of a closed polygonal chain are called its '' edges'' or ''sides''. The points where two edges meet are the polygon ...
s and higher. A truncation removes vertices, and inserts a new facet in place of each former vertex. Faces are truncated, doubling their edges. (The term, coined by Kepler
Johannes Kepler (27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best known for his laws of p ...
, comes from Latin ''truncare'' 'to cut off'.)
#: polyhedra
In geometry, a polyhedron (: polyhedra or polyhedrons; ) is a three-dimensional figure with flat polygonal faces, straight edges and sharp corners or vertices. The term "polyhedron" may refer either to a solid figure or to its boundary su ...
and higher. It can be seen as rectifying its rectification. A cantellation truncates both vertices and edges and replaces them with new facets. Cells are replaced by topologically expanded copies of themselves. (The term, coined by Johnson, is derived from the verb ''cant'', like ''bevel
A bevelled edge (UK) or beveled edge (US) is an edge of a structure that is not perpendicular to the faces of the piece. The words bevel and chamfer overlap in usage; in general usage, they are often interchanged, while in technical usage, they ...
'', meaning to cut with a slanted face.)
#: polyhedra
In geometry, a polyhedron (: polyhedra or polyhedrons; ) is a three-dimensional figure with flat polygonal faces, straight edges and sharp corners or vertices. The term "polyhedron" may refer either to a solid figure or to its boundary su ...
and higher. It can be seen as truncating its rectification. A cantitruncation truncates both vertices and edges and replaces them with new facets. Cells are replaced by topologically expanded copies of themselves. (The composite term combines cantellation and truncation)
#** There are higher cantellations also: bicantitruncation t1,2,3 or t2r, tricantitruncation t2,3,4 or t3r, quadricantitruncation t3,4,5 or t4r, etc.
# t0,3: Runcination - applied to Uniform 4-polytope
In geometry, a uniform 4-polytope (or uniform polychoron) is a 4-dimensional polytope which is vertex-transitive and whose cells are uniform polyhedron, uniform polyhedra, and faces are regular polygons.
There are 47 non-Prism (geometry), prism ...
and higher. Runcination truncates vertices, edges, and faces, replacing them each with new facets. 4-faces are replaced by topologically expanded copies of themselves. (The term, coined by Johnson, is derived from Latin ''runcina'' 'carpenter's plane'.)
#* There are higher runcinations also: biruncination t1,4, triruncination t2,5, etc.
# t0,4 or 2r2r: Sterication - applied to Uniform 5-polytope
In geometry, a uniform 5-polytope is a five-dimensional uniform polytope. By definition, a uniform 5-polytope is vertex-transitive and constructed from uniform 4-polytope Facet (geometry), facets.
The complete set of convex uniform 5-polytopes ...
s and higher. It can be seen as birectifying its birectification. Sterication truncates vertices, edges, faces, and cells, replacing each with new facets. 5-faces are replaced by topologically expanded copies of themselves. (The term, coined by Johnson, is derived from Greek ''stereos'' 'solid'.)
#* There are higher sterications also: bisterication t1,5 or 2r3r, tristerication t2,6 or 2r4r, etc.
#* t0,2,4 or 2t2r: Stericantellation - applied to Uniform 5-polytope
In geometry, a uniform 5-polytope is a five-dimensional uniform polytope. By definition, a uniform 5-polytope is vertex-transitive and constructed from uniform 4-polytope Facet (geometry), facets.
The complete set of convex uniform 5-polytopes ...
s and higher. It can be seen as bitruncating its birectification.
#** There are higher sterications also: bistericantellation t1,3,5 or 2t3r, tristericantellation t2,4,6 or 2t4r, etc.
# t0,5: Pentellation - applied to Uniform 6-polytopes and higher. Pentellation truncates vertices, edges, faces, cells, and 4-faces, replacing each with new facets. 6-faces are replaced by topologically expanded copies of themselves. (Pentellation is derived from Greek ''pente
Pente is an Abstract strategy game, abstract strategy board game for two or more players, created in 1977 by Gary Gabrel. A member of the M,n,k-game, m,n,k game family, Pente stands out for its Custodian capture, custodial capture mechanic, which ...
'' 'five'.)
#* There are also higher pentellations: bipentellation t1,6, tripentellation t2,7, etc.
# t0,6 or 3r3r: Hexication - applied to Uniform 7-polytopes and higher. It can be seen as trirectifying its trirectification. Hexication truncates vertices, edges, faces, cells, 4-faces, and 5-faces, replacing each with new facets. 7-faces are replaced by topologically expanded copies of themselves. (Hexication is derived from Greek '' hex'' 'six'.)
#* There are higher hexications also: bihexication: t1,7 or 3r4r, trihexication: t2,8 or 3r5r, etc.
#* t0,3,6 or 3t3r: Hexiruncinated - applied to Uniform 7-polytopes and higher. It can be seen as tritruncating its trirectification.
#** There are also higher hexiruncinations: bihexiruncinated: t1,4,7 or 3t4r, trihexiruncinated: t2,5,8 or 3t5r, etc.
# t0,7: Heptellation - applied to Uniform 8-polytopes and higher. Heptellation truncates vertices, edges, faces, cells, 4-faces, 5-faces, and 6-faces, replacing each with new facets. 8-faces are replaced by topologically expanded copies of themselves. (Heptellation is derived from Greek '' hepta'' 'seven'.)
#* There are higher heptellations also: biheptellation t1,8, triheptellation t2,9, etc.
# t0,8 or 4r4r: Octellation - applied to Uniform 9-polytopes and higher.
# t0,9: Ennecation - applied to Uniform 10-polytopes and higher.
In addition combinations of truncations can be performed which also generate new uniform polytopes. For example, a ''runcitruncation'' is a ''runcination'' and ''truncation'' applied together.
If all truncations are applied at once, the operation can be more generally called an omnitruncation
In geometry, an omnitruncation of a convex polytope is a simple polytope of the same dimension, having a vertex for each flag of the original polytope and a facet for each face of any dimension of the original polytope. Omnitruncation is the dual ...
.
Alternation
hypercube
In geometry, a hypercube is an ''n''-dimensional analogue of a square ( ) and a cube ( ); the special case for is known as a ''tesseract''. It is a closed, compact, convex figure whose 1- skeleton consists of groups of opposite parallel l ...
s are known as demicubes. In three dimensions, this produces a tetrahedron
In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular Face (geometry), faces, six straight Edge (geometry), edges, and four vertex (geometry), vertices. The tet ...
; in four dimensions, this produces a 16-cell
In geometry, the 16-cell is the regular convex 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the ...
, or ''demitesseract''.
Vertex figure
Uniform polytopes can be constructed from theirvertex figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a general -polytope is sliced off.
Definitions
Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connected ed ...
, the arrangement of edges, faces, cells, etc. around each vertex. Uniform polytopes represented by a Coxeter diagram
Harold Scott MacDonald "Donald" Coxeter (9 February 1907 – 31 March 2003) was a British-Canadian geometer and mathematician. He is regarded as one of the greatest geometers of the 20th century.
Coxeter was born in England and educated ...
, marking active mirrors by rings, have reflectional symmetry, and can be simply constructed by recursive reflections of the vertex figure.
A smaller number of nonreflectional uniform polytopes have a single vertex figure but are not repeated by simple reflections. Most of these can be represented with operations like alternation of other uniform polytopes.
Vertex figures for single-ringed Coxeter diagrams can be constructed from the diagram by removing the ringed node, and ringing neighboring nodes. Such vertex figures are themselves vertex-transitive.
Multiringed polytopes can be constructed by a slightly more complicated construction process, and their topology is not a uniform polytope. For example, the vertex figure of a truncated regular polytope (with 2 rings) is a pyramid. An omnitruncated
In geometry, an omnitruncation of a convex polytope is a simple polytope of the same dimension, having a vertex for each Flag (geometry), flag of the original polytope and a Facet (geometry), facet for each face of any dimension of the original pol ...
polytope (all nodes ringed) will always have an irregular simplex
In geometry, a simplex (plural: simplexes or simplices) is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. ...
as its vertex figure.
Circumradius
Uniform polytopes have equal edge-lengths, and all vertices are an equal distance from the center, called the circumradius. Uniform polytopes whose circumradius is equal to the edge length can be used asvertex figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a general -polytope is sliced off.
Definitions
Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connected ed ...
s for uniform honeycombs. For example, the regular hexagon
In geometry, a hexagon (from Greek , , meaning "six", and , , meaning "corner, angle") is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.
Regular hexagon
A regular hexagon is de ...
divides into 6 equilateral triangles and is the vertex figure for the regular triangular tiling
In geometry, the triangular tiling or triangular tessellation is one of the three regular tilings of the Euclidean plane, and is the only such tiling where the constituent shapes are not parallelogons. Because the internal angle of the equilater ...
. Also the cuboctahedron
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertex (geometry), vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edge (geometry), edges, each separating a tr ...
divides into 8 regular tetrahedra and 6 square pyramids (half octahedron
In geometry, an octahedron (: octahedra or octahedrons) is any polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Many types of i ...
), and it is the vertex figure for the alternated cubic honeycomb.
Uniform polytopes by dimension
It is useful to classify the uniform polytopes by dimension. This is equivalent to the number of nodes on the Coxeter diagram, or the number of hyperplanes in the Wythoffian construction. Because (''n''+1)-dimensional polytopes are tilings of ''n''-dimensional spherical space, tilings of ''n''-dimensional Euclidean andhyperbolic space
In mathematics, hyperbolic space of dimension ''n'' is the unique simply connected, ''n''-dimensional Riemannian manifold of constant sectional curvature equal to −1.
It is homogeneous, and satisfies the stronger property of being a symme ...
are also considered to be (''n''+1)-dimensional. Hence, the tilings of two-dimensional space are grouped with the three-dimensional solids.
One dimension
The only one-dimensional polytope is the line segment. It corresponds to the Coxeter family A1.Two dimensions
In two dimensions, there is an infinite family of convex uniform polytopes, theregular polygon
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either ''convex ...
s, the simplest being the equilateral triangle
A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called ''vertices'', are zero-dimensional points while the sides connecting them, also called ''edges'', are one-dimension ...
. Truncated regular polygons become bicolored geometrically quasiregular polygons of twice as many sides, t=. The first few regular polygons (and quasiregular forms) are displayed below:
There is also an infinite set of star polygon
In geometry, a star polygon is a type of non-convex polygon. Regular star polygons have been studied in depth; while star polygons in general appear not to have been formally defined, Decagram (geometry)#Related figures, certain notable ones can ...
s (one for each rational number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (for example,
The set of all ...
greater than 2), but these are non-convex. The simplest example is the pentagram
A pentagram (sometimes known as a pentalpha, pentangle, or star pentagon) is a regular five-pointed star polygon, formed from the diagonal line segments of a convex (or simple, or non-self-intersecting) regular pentagon. Drawing a circle around ...
, which corresponds to the rational number 5/2. Regular star polygons, , can be truncated into semiregular star polygons, t=t, but become double-coverings if ''q'' is even. A truncation can also be made with a reverse orientation polygon t=, for example t=.
Regular polygons, represented by Schläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines List of regular polytopes and compounds, regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, wh ...
for a p-gon. Regular polygons are self-dual, so the rectification produces the same polygon. The uniform truncation operation doubles the sides to . The snub operation, alternating the truncation, restores the original polygon . Thus all uniform polygons are also regular. The following operations can be performed on regular polygons to derive the uniform polygons, which are also regular polygons:
Three dimensions
In three dimensions, the situation gets more interesting. There are five convex regular polyhedra, known as thePlatonic solid
In geometry, a Platonic solid is a Convex polytope, convex, regular polyhedron in three-dimensional space, three-dimensional Euclidean space. Being a regular polyhedron means that the face (geometry), faces are congruence (geometry), congruent (id ...
s:
In addition to these, there are also 13 semiregular polyhedra, or Archimedean solid
The Archimedean solids are a set of thirteen convex polyhedra whose faces are regular polygon and are vertex-transitive, although they aren't face-transitive. The solids were named after Archimedes, although he did not claim credit for them. They ...
s, which can be obtained via Wythoff construction
In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.
Construction process ...
s, or by performing operations such as truncation
In mathematics and computer science, truncation is limiting the number of digits right of the decimal point.
Truncation and floor function
Truncation of positive real numbers can be done using the floor function. Given a number x \in \mathbb ...
on the Platonic solids, as demonstrated in the following table:
There is also the infinite set of prisms, one for each regular polygon, and a corresponding set of antiprism
In geometry, an antiprism or is a polyhedron composed of two Parallel (geometry), parallel Euclidean group, direct copies (not mirror images) of an polygon, connected by an alternating band of triangles. They are represented by the Conway po ...
s.
The uniform star polyhedra include a further 4 regular star polyhedra, the Kepler-Poinsot polyhedra, and 53 semiregular star polyhedra. There are also two infinite sets, the star prisms (one for each star polygon) and star antiprisms (one for each rational number greater than 3/2).
Constructions
The Wythoffian uniform polyhedra and tilings can be defined by their Wythoff symbol, which specifies the fundamental region of the object. An extension of Schläfli notation, also used by Coxeter, applies to all dimensions; it consists of the letter 't', followed by a series of subscripted numbers corresponding to the ringed nodes of theCoxeter diagram
Harold Scott MacDonald "Donald" Coxeter (9 February 1907 – 31 March 2003) was a British-Canadian geometer and mathematician. He is regarded as one of the greatest geometers of the 20th century.
Coxeter was born in England and educated ...
, and followed by the Schläfli symbol of the regular seed polytope. For example, the truncated octahedron
In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces (8 regular hexagon, hexagons and 6 Squa ...
is represented by the notation: t0,1.
Four dimensions
In four dimensions, there are 6convex regular 4-polytope
In mathematics, a regular 4-polytope or regular polychoron is a regular four-dimensional polytope. They are the four-dimensional analogues of the regular polyhedra in three dimensions and the regular polygons in two dimensions.
There are six co ...
s, 17 prisms on the Platonic and Archimedean solids (excluding the cube-prism, which has already been counted as the tesseract
In geometry, a tesseract or 4-cube is a four-dimensional hypercube, analogous to a two-dimensional square and a three-dimensional cube. Just as the perimeter of the square consists of four edges and the surface of the cube consists of six ...
), and two infinite sets: the prisms on the convex antiprisms, and the duoprism
In geometry of 4 dimensions or higher, a double prism or duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher. The Cartesian product of an -polytope and an -polytope is an -polytope, wher ...
s. There are also 41 convex semiregular 4-polytope, including the non-Wythoffian grand antiprism
In geometry, the grand antiprism or pentagonal double antiprismoid is a uniform 4-polytope (4-dimensional uniform polytope) bounded by 320 cells: 20 pentagonal antiprisms, and 300 tetrahedra. It is an anomalous, non-Wythoffian uniform 4-polyto ...
and the snub 24-cell
In geometry, the snub 24-cell or snub disicositetrachoron is a convex uniform 4-polytope composed of 120 regular Tetrahedron, tetrahedral and 24 Regular icosahedron, icosahedral cell (mathematics), cells. Five tetrahedra and three icosahedra meet ...
. Both of these special 4-polytope are composed of subgroups of the vertices of the 600-cell
In geometry, the 600-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol .
It is also known as the C600, hexacosichoron and hexacosihedroid.
It is also called a tetraplex (abbreviated from ...
.
The four-dimensional uniform star polytopes have not all been enumerated. The ones that have include the 10 regular star (Schläfli-Hess) 4-polytopes and 57 prisms on the uniform star polyhedra, as well as three infinite families: the prisms on the star antiprisms, the duoprisms formed by multiplying
Multiplication is one of the four elementary mathematical operations of arithmetic, with the other ones being addition, subtraction, and division. The result of a multiplication operation is called a '' product''. Multiplication is often de ...
two star polygons, and the duoprisms formed by multiplying an ordinary polygon with a star polygon. There is an unknown number of 4-polytope that do not fit into the above categories; over one thousand have been discovered so far.

 Every regular polytope can be seen as the images of a fundamental region in a small number of mirrors. In a 4-dimensional polytope (or 3-dimensional cubic honeycomb) the fundamental region is bounded by four mirrors. A mirror in 4-space is a three-dimensional
Every regular polytope can be seen as the images of a fundamental region in a small number of mirrors. In a 4-dimensional polytope (or 3-dimensional cubic honeycomb) the fundamental region is bounded by four mirrors. A mirror in 4-space is a three-dimensional hyperplane
In geometry, a hyperplane is a generalization of a two-dimensional plane in three-dimensional space to mathematical spaces of arbitrary dimension. Like a plane in space, a hyperplane is a flat hypersurface, a subspace whose dimension is ...
, but it is more convenient for our purposes to consider only its two-dimensional intersection with the three-dimensional surface of the hypersphere
In mathematics, an -sphere or hypersphere is an - dimensional generalization of the -dimensional circle and -dimensional sphere to any non-negative integer .
The circle is considered 1-dimensional and the sphere 2-dimensional because a point ...
; thus the mirrors form an irregular tetrahedron
In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular Face (geometry), faces, six straight Edge (geometry), edges, and four vertex (geometry), vertices. The tet ...
.
Each of the sixteen regular 4-polytopes
In mathematics, a regular 4-polytope or regular polychoron is a regular polytope, regular 4-polytope, four-dimensional polytope. They are the four-dimensional analogues of the Regular polyhedron, regular polyhedra in three dimensions and the regul ...
is generated by one of four symmetry groups, as follows:
* group ,3,3 the 5-cell
In geometry, the 5-cell is the convex 4-polytope with Schläfli symbol . It is a 5-vertex four-dimensional space, four-dimensional object bounded by five tetrahedral cells. It is also known as a C5, hypertetrahedron, pentachoron, pentatope, pe ...
, which is self-dual;
* group ,3,4 16-cell
In geometry, the 16-cell is the regular convex 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the ...
and its dual tesseract
In geometry, a tesseract or 4-cube is a four-dimensional hypercube, analogous to a two-dimensional square and a three-dimensional cube. Just as the perimeter of the square consists of four edges and the surface of the cube consists of six ...
;
* group ,4,3 the 24-cell
In four-dimensional space, four-dimensional geometry, the 24-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also called C24, or the icositetrachoron, octaplex (short for "octa ...
, self-dual;
* group ,3,5 600-cell
In geometry, the 600-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol .
It is also known as the C600, hexacosichoron and hexacosihedroid.
It is also called a tetraplex (abbreviated from ...
, its dual 120-cell
In geometry, the 120-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also called a C120, dodecaplex (short for "dodecahedral complex"), hyperdodecahedron, polydodecahedron, hec ...
, and their ten regular stellations.
* group 1,1,1 contains only repeated members of the ,3,4family.
(The groups are named in Coxeter notation
In geometry, Coxeter notation (also Coxeter symbol) is a system of classifying symmetry groups, describing the angles between fundamental reflections of a Coxeter group in a bracketed notation expressing the structure of a Coxeter-Dynkin diagram, ...
.)
Eight of the convex uniform honeycomb
In geometry, a convex uniform honeycomb is a uniform polytope, uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex polyhedron, convex uniform polyhedron, uniform polyhedral cells.
Twenty-eight such honey ...
s in Euclidean 3-space are analogously generated from the cubic honeycomb
The cubic honeycomb or cubic cellulation is the only proper regular space-filling tessellation (or honeycomb (geometry), honeycomb) in Euclidean 3-space made up of cube, cubic cells. It has 4 cubes around every edge, and 8 cubes around each verte ...
, by applying the same operations used to generate the Wythoffian uniform 4-polytopes.
For a given symmetry simplex, a generating point may be placed on any of the four vertices, 6 edges, 4 faces, or the interior volume. On each of these 15 elements there is a point whose images, reflected in the four mirrors, are the vertices of a uniform 4-polytope.
The extended Schläfli symbols are made by a t followed by inclusion of one to four subscripts 0,1,2,3. If there is one subscript, the generating point is on a corner of the fundamental region, i.e. a point where three mirrors meet. These corners are notated as
* 0: vertex of the parent 4-polytope (center of the dual's cell)
* 1: center of the parent's edge (center of the dual's face)
* 2: center of the parent's face (center of the dual's edge)
* 3: center of the parent's cell (vertex of the dual)
(For the two self-dual 4-polytopes, "dual" means a similar 4-polytope in dual position.) Two or more subscripts mean that the generating point is between the corners indicated.
Constructive summary
The 15 constructive forms by family are summarized below. The self-dual families are listed in one column, and others as two columns with shared entries on the symmetricCoxeter diagram
Harold Scott MacDonald "Donald" Coxeter (9 February 1907 – 31 March 2003) was a British-Canadian geometer and mathematician. He is regarded as one of the greatest geometers of the 20th century.
Coxeter was born in England and educated ...
s. The final 10th row lists the snub 24-cell constructions. This includes all nonprismatic uniform 4-polytopes, except for the non-Wythoffian grand antiprism
In geometry, the grand antiprism or pentagonal double antiprismoid is a uniform 4-polytope (4-dimensional uniform polytope) bounded by 320 cells: 20 pentagonal antiprisms, and 300 tetrahedra. It is an anomalous, non-Wythoffian uniform 4-polyto ...
, which has no Coxeter family.
Truncated forms
The following table defines 15 forms of truncation. Each form can have from one to four cell types, located in positions 0,1,2,3 as defined above. The cells are labeled by polyhedral truncation notation. * An n-gonal prism is represented as : ×. * The green background is shown on forms that are equivalent to either the parent or the dual. * The red background shows the truncations of the parent, and blue the truncations of the dual.Half forms
Half constructions exist with ''holes'' rather than ringed nodes. Branches neighboring ''holes'' and inactive nodes must be even-order. Half construction have the vertices of an identically ringed construction.Five and higher dimensions
In five and higher dimensions, there are 3 regular polytopes, thehypercube
In geometry, a hypercube is an ''n''-dimensional analogue of a square ( ) and a cube ( ); the special case for is known as a ''tesseract''. It is a closed, compact, convex figure whose 1- skeleton consists of groups of opposite parallel l ...
, simplex
In geometry, a simplex (plural: simplexes or simplices) is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. ...
and cross-polytope
In geometry, a cross-polytope, hyperoctahedron, orthoplex, staurotope, or cocube is a regular, convex polytope that exists in ''n''- dimensional Euclidean space. A 2-dimensional cross-polytope is a square, a 3-dimensional cross-polytope is a reg ...
. They are generalisations of the three-dimensional cube, tetrahedron and octahedron, respectively. There are no regular star polytopes in these dimensions. Most uniform higher-dimensional polytopes are obtained by modifying the regular polytopes, or by taking the Cartesian product of polytopes of lower dimensions.
In six, seven and eight dimensions, the exceptional
Exception(s), The Exception(s), or exceptional may refer to:
Arts and entertainment
* '' The Exception'', a 2016 British film
* ''The Exception'' (2006 novel), a Danish novel (orig. ''Undtagelsen'', 2004) by Christian Jungersen
* ''The Excep ...
simple Lie group
In mathematics, a simple Lie group is a connected non-abelian Lie group ''G'' which does not have nontrivial connected normal subgroups. The list of simple Lie groups can be used to read off the list of simple Lie algebras and Riemannian symm ...
s, E6, E7 and E8 come into play. By placing rings on a nonzero number of nodes of the Coxeter diagram
Harold Scott MacDonald "Donald" Coxeter (9 February 1907 – 31 March 2003) was a British-Canadian geometer and mathematician. He is regarded as one of the greatest geometers of the 20th century.
Coxeter was born in England and educated ...
s, one can obtain 39 new 6-polytopes, 127 new 7-polytopes and 255 new 8-polytopes. A notable example is the 421 polytope.
Uniform honeycombs
Related to the subject of finite uniform polytopes are uniform honeycombs in Euclidean and hyperbolic spaces. Euclidean uniform honeycombs are generated by affine Coxeter groups and hyperbolic honeycombs are generated by the hyperbolic Coxeter groups. Two affine Coxeter groups can be multiplied together. There are two classes of hyperbolic Coxeter groups, compact and paracompact. Uniform honeycombs generated by compact groups have finite facets and vertex figures, and exist in 2 through 4 dimensions. Paracompact groups have affine or hyperbolic subgraphs, and infinite facets or vertex figures, and exist in 2 through 10 dimensions.See also
*Schläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines List of regular polytopes and compounds, regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, wh ...
References
* Coxeter ''The Beauty of Geometry: Twelve Essays'', Dover Publications, 1999, (Chapter 3: Wythoff's Construction for Uniform Polytopes) * Norman Johnson ''Uniform Polytopes'', Manuscript (1991) ** Norman Johnson: ''The Theory of Uniform Polytopes and Honeycombs'', Ph.D. Dissertation, University of Toronto, 196ONLINE
* A. Boole Stott: ''Geometrical deduction of semiregular from regular polytopes and space fillings'', Verhandelingen of the Koninklijke academy van Wetenschappen width unit Amsterdam, Eerste Sectie 11,1, Amsterdam, 191
* H.S.M. Coxeter: ** H.S.M. Coxeter, M.S. Longuet-Higgins and J.C.P. Miller: ''Uniform Polyhedra'', Philosophical Transactions of the Royal Society of London, Londne, 195
** H.S.M. Coxeter, ''Regular Polytopes'', 3rd Edition, Dover New York, 1973 *
', edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ** (Paper 22) H.S.M. Coxeter
Regular and Semi Regular Polytopes I
ath. Zeit. 46 (1940) 380-407, MR 2,10** (Paper 23) H.S.M. Coxeter
Regular and Semi-Regular Polytopes II
ath. Zeit. 188 (1985) 559-591** (Paper 24) H.S.M. Coxeter
Regular and Semi-Regular Polytopes III
ath. Zeit. 200 (1988) 3-45* Marco Möller, ''Vierdimensionale Archimedische Polytope'', Dissertation, Universität Hamburg, Hamburg (2004)
ONLINE
External links
*uniform, convex polytopes in four dimensions:
Marco Möller {{Polytopes Uniform polytopes