Sieve Of Eratosthenes

In mathematics, the sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to any given limit.

It does so by iteratively marking as composite (i.e., not prime) the multiples of each prime, starting with the first prime number, 2. The multiples of a given prime are generated as a sequence of numbers starting from that prime, with constant difference between them that is equal to that prime.Horsley, Rev. Samuel, F. R. S., "' or, The Sieve of Eratosthenes. Being an account of his method of finding all the Prime Numbers,
''Philosophical Transactions'' (1683–1775), Vol. 62. (1772), pp. 327–347
This is the sieve's key distinction from using trial division to sequentially test each candidate number for divisibility by each prime. Once all the multiples of each discovered prime have been marked as composites, the remaining unmarked numbers are primes.

The earliest known reference to the sieve (, ''kóskinon Eratosthénous'') is in Nicomachus of Gerasa's ''Introduction to Arithmetic'', an early 2nd century CE book which attributes it to Eratosthenes of Cyrene, a 3rd century BCE Greek mathematician, though describing the sieving by odd numbers instead of by primes.

One of a number of prime number sieves, it is one of the most efficient ways to find all of the smaller primes. It may be used to find primes in arithmetic progressions.

Overview

A prime number is a natural number that has exactly two distinct natural number divisors: the number 1 and itself.

To find all the prime numbers less than or equal to a given integer by Eratosthenes' method:

# Create a list of consecutive integers from 2 through : .
# Initially, let equal 2, the smallest prime number.
# Enumerate the multiples of by counting in increments of from to , and mark them in the list (these will be ; the itself should not be marked).
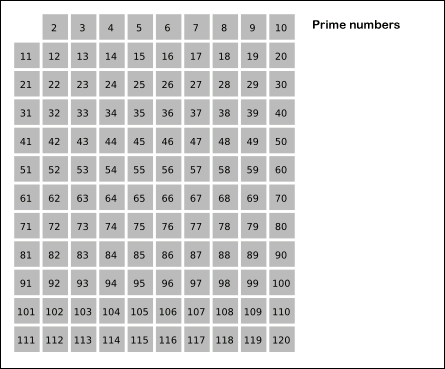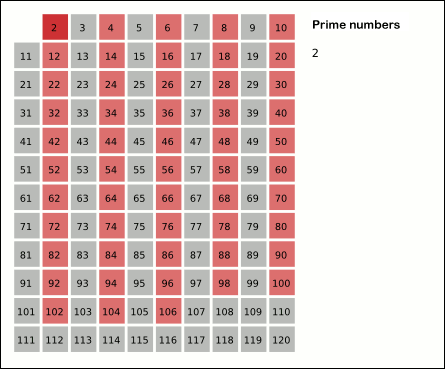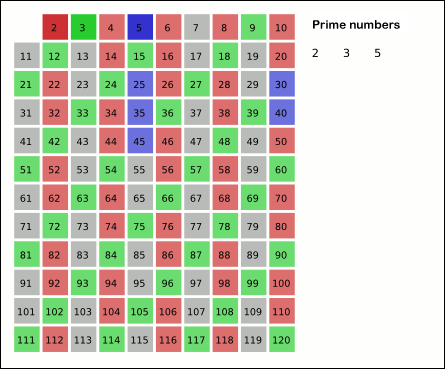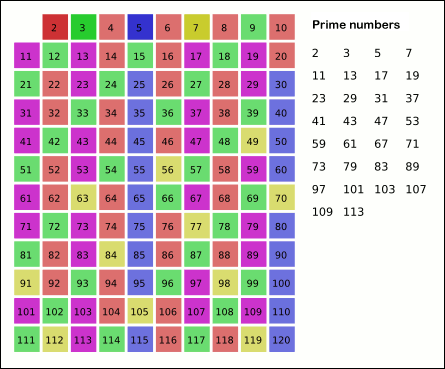
# Find the smallest number in the list greater than that is not marked. If there was no such number, stop. Otherwise, let now equal this new number (which is the next prime), and repeat from step 3.
# When the algorithm terminates, the numbers remaining not marked in the list are all the primes below .

The main idea here is that every value given to will be prime, because if it were composite it would be marked as a multiple of some other, smaller prime. Note that some of the numbers may be marked more than once (e.g., 15 will be marked both for 3 and 5).

As a refinement, it is sufficient to mark the numbers in step 3 starting from , as all the smaller multiples of will have already been marked at that point. This means that the algorithm is allowed to terminate in step 4 when is greater than .

Another refinement is to initially list odd numbers only, , and count in increments of in step 3, thus marking only odd multiples of . This actually appears in the original algorithm. This can be generalized with wheel factorization, forming the initial list only from numbers coprime with the first few primes and not just from odds (i.e., numbers coprime with 2), and counting in the correspondingly adjusted increments so that only such multiples of are generated that are coprime with those small primes, in the first place.

Example

To find all the prime numbers less than or equal to 30, proceed as follows.

First, generate a list of integers from 2 to 30:

 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

The first number in the list is 2; cross out every 2nd number in the list after 2 by counting up from 2 in increments of 2 (these will be all the multiples of 2 in the list):

 2 3 5 7 9 11 13 15 17 19 21 23 25 27 29

The next number in the list after 2 is 3; cross out every 3rd number in the list after 3 by counting up from 3 in increments of 3 (these will be all the multiples of 3 in the list):

 2 3 5 7 11 13 17 19 23 25 29

The next number not yet crossed out in the list after 3 is 5; cross out every 5th number in the list after 5 by counting up from 5 in increments of 5 (i.e. all the multiples of 5):

 2 3 5 7 11 13 17 19 23 29

The next number not yet crossed out in the list after 5 is 7; the next step would be to cross out every 7th number in the list after 7, but they are all already crossed out at this point, as these numbers (14, 21, 28) are also multiples of smaller primes because 7 × 7 is greater than 30. The numbers not crossed out at this point in the list are all the prime numbers below 30:

 2 3 5 7 11 13 17 19 23 29

Algorithm and variants

Pseudocode

The sieve of Eratosthenes can be expressed in pseudocode, as follows:, p. 16.Jonathan Sorenson, ''An Introduction to Prime Number Sieves''
Computer Sciences Technical Report #909, Department of Computer Sciences University of Wisconsin-Madison, January 2, 1990 (the use of optimization of starting from squares, and thus using only the numbers whose square is below the upper limit, is shown).

algorithm Sieve of Eratosthenes is
input: an integer ''n'' > 1.
output: all prime numbers from 2 through ''n''.

let ''A'' be an array of Boolean values, indexed by integers 2 to ''n'',
initially all set to true.

for ''i'' = 2, 3, 4, ..., not exceeding do
if ''A'' 'i''is true
for ''j'' = ''i''², ''i''²+''i'', ''i''²+2''i'', ''i''²+3''i'', ..., not exceeding ''n'' do
set ''A'' 'j'':= false

return all ''i'' such that ''A'' 'i''is true.

This algorithm produces all primes not greater than . It includes a common optimization, which is to start enumerating the multiples of each prime from . The time complexity of this algorithm is , provided the array update is an operation, as is usually the case.

Segmented sieve

As Sorenson notes, the problem with the sieve of Eratosthenes is not the number of operations it performs but rather its memory requirements. For large , the range of primes may not fit in memory; worse, even for moderate , its cache use is highly suboptimal. The algorithm walks through the entire array , exhibiting almost no locality of reference.

A solution to these problems is offered by ''segmented'' sieves, where only portions of the range are sieved at a time. These have been known since the 1970s, and work as follows:

# Divide the range 2 through into segments of some size .
# Find the primes in the first (i.e. the lowest) segment, using the regular sieve.
# For each of the following segments, in increasing order, with being the segment's topmost value, find the primes in it as follows:
## Set up a Boolean array of size .
## Mark as non-prime the positions in the array corresponding to the multiples of each prime found so far, by enumerating its multiples in steps of starting from the lowest multiple of between and .
## The remaining non-marked positions in the array correspond to the primes in the segment. It is not necessary to mark any multiples of ''these'' primes, because all of these primes are larger than , as for , one has $(k\Delta + 1)^2 > (k+1)\Delta$.

If is chosen to be , the space complexity of the algorithm is , while the time complexity is the same as that of the regular sieve.

For ranges with upper limit so large that the sieving primes below as required by the page segmented sieve of Eratosthenes cannot fit in memory, a slower but much more space-efficient sieve like the pseudosquares prime sieve, developed by Jonathan P. Sorenson, can be used instead.

Incremental sieve

An incremental formulation of the sieveO'Neill, Melissa E.
"The Genuine Sieve of Eratosthenes"
''Journal of Functional Programming'', published online by Cambridge University Press 9 October 2008 , pp. 10, 11 (contains two incremental sieves in Haskell: a priority-queue–based one by O'Neill and a list–based, by Richard Bird). generates primes indefinitely (i.e., without an upper bound) by interleaving the generation of primes with the generation of their multiples (so that primes can be found in gaps between the multiples), where the multiples of each prime are generated directly by counting up from the square of the prime in increments of (or for odd primes). The generation must be initiated only when the prime's square is reached, to avoid adverse effects on efficiency. It can be expressed symbolically under the dataflow paradigm as

''primes'' = '2'', ''3'', ...\ ''p''², ''p''²+''p'', ...for ''p'' in ''primes''],

using list comprehension notation with \ denoting set subtraction of arithmetic progressions of numbers.

Primes can also be produced by iteratively sieving out the composites through divisibility testing by sequential primes, one prime at a time. It is not the sieve of Eratosthenes but is often confused with it, even though the sieve of Eratosthenes directly generates the composites instead of testing for them. Trial division has worse theoretical complexity than that of the sieve of Eratosthenes in generating ranges of primes.

When testing each prime, the ''optimal'' trial division algorithm uses all prime numbers not exceeding its square root, whereas the sieve of Eratosthenes produces each composite from its prime factors only, and gets the primes "for free", between the composites. The widely known 1975 functional sieve code by David Turner is often presented as an example of the sieve of Eratosthenes but is actually a sub-optimal trial division sieve.

Algorithmic complexity

The sieve of Eratosthenes is a popular way to benchmark computer performance. The time complexity of calculating all primes below in the random access machine model is operations, a direct consequence of the fact that the prime harmonic series asymptotically approaches . It has an exponential time complexity with regard to length of the input, though, which makes it a pseudo-polynomial algorithm. The basic algorithm requires of memory.

The bit complexity of the algorithm is bit operations with a memory requirement of .

The normally implemented page segmented version has the same operational complexity of as the non-segmented version but reduces the space requirements to the very minimal size of the segment page plus the memory required to store the base primes less than the square root of the range used to cull composites from successive page segments of size .

A special (rarely, if ever, implemented) segmented version of the sieve of Eratosthenes, with basic optimizations, uses operations and bits of memory.Paul Pritchard, "A sublinear additive sieve for finding prime numbers", ''Communications of the ACM'' 24 (1981), 18–23. Paul Pritchard, Explaining the wheel sieve, Acta Informatica 17 (1982), 477–485. Paul Pritchard, "Fast compact prime number sieves" (among others), ''Journal of Algorithms'' 4
(1983), 332–344.

Using big O notation ignores constant factors and offsets that may be very significant for practical ranges: The sieve of Eratosthenes variation known as the Pritchard wheel sieve has an performance, but its basic implementation requires either a "one large array" algorithm which limits its usable range to the amount of available memory else it needs to be page segmented to reduce memory use. When implemented with page segmentation in order to save memory, the basic algorithm still requires about bits of memory (much more than the requirement of the basic page segmented sieve of Eratosthenes using bits of memory). Pritchard's work reduced the memory requirement at the cost of a large constant factor. Although the resulting wheel sieve has performance and an acceptable memory requirement, it is not faster than a reasonably Wheel Factorized basic sieve of Eratosthenes for practical sieving ranges.

Euler's sieve

Euler's proof of the zeta product formula contains a version of the sieve of Eratosthenes in which each composite number is eliminated exactly once. The same sieve was rediscovered and observed to take linear time by .. It, too, starts with a list of numbers from 2 to in order. On each step the first element is identified as the next prime, is multiplied with each element of the list (thus starting with itself), and the results are marked in the list for subsequent deletion. The initial element and the marked elements are then removed from the working sequence, and the process is repeated:

  (3) 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59 61 63 65 67 69 71 73 75 77 79 ...
  (5) 7 11 13 17 19 23 25 29 31 35 37 41 43 47 49 53 55 59 61 65 67 71 73 77 79 ...
  (7) 11 13 17 19 23 29 31 37 41 43 47 49 53 59 61 67 71 73 77 79 ...
  (11) 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 ...
  ..

Here the example is shown starting from odds, after the first step of the algorithm. Thus, on the th step all the remaining multiples of the th prime are removed from the list, which will thereafter contain only numbers coprime with the first primes (cf. wheel factorization), so that the list will start with the next prime, and all the numbers in it below the square of its first element will be prime too.

Thus, when generating a bounded sequence of primes, when the next identified prime exceeds the square root of the upper limit, all the remaining numbers in the list are prime. In the example given above that is achieved on identifying 11 as next prime, giving a list of all primes less than or equal to 80.

Note that numbers that will be discarded by a step are still used while marking the multiples in that step, e.g., for the multiples of 3 it is , , , , ..., , ..., so care must be taken dealing with this.

See also

* Sieve of Pritchard
* Sieve of Atkin
* Sieve of Sundaram
* Sieve theory

References

External links

primesieve – Very fast highly optimized C/C++ segmented Sieve of Eratosthenes

''Eratosthenes, sieve of'' at Encyclopaedia of Mathematics



Sieve of Eratosthenes
by George Beck, Wolfram Demonstrations Project.

Sieve of Eratosthenes in Haskell

Sieve of Eratosthenes algorithm illustrated and explained. Java and C++ implementations.

Fast optimized highly parallel CUDA segmented Sieve of Eratosthenes in C

SieveOfEratosthenesInManyProgrammingLanguages c2 wiki page


Sieve of Eratosthenes in C from 1998 with nice features and algorithmic tricks explained.

{{DEFAULTSORT:Sieve Of Eratosthenes
Primality tests
Articles with example pseudocode

Algorithms