|
Composite Number
A composite number is a positive integer that can be formed by multiplying two smaller positive integers. Accordingly it is a positive integer that has at least one divisor other than 1 and itself. Every positive integer is composite, prime number, prime, or the Unit (ring theory), unit 1, so the composite numbers are exactly the numbers that are not prime and not a unit. E.g., the integer 14 is a composite number because it is the product of the two smaller integers 2 × 7 but the integers 2 and 3 are not because each can only be divided by one and itself. The composite numbers up to 150 are: :4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100, 102, 104, 105, 106, 108, 110, 111, 112, 114, 115, 116, 117, 118, 119, 120, 121, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Highly Composite Number
A highly composite number is a positive integer that has more divisors than all smaller positive integers. If ''d''(''n'') denotes the number of divisors of a positive integer ''n'', then a positive integer ''N'' is highly composite if ''d''(''N'') > ''d''(''n'') for all ''n'' < ''N''. For example, 6 is highly composite because ''d''(6)=4, and for ''n''=1,2,3,4,5, you get ''d''(''n'')=1,2,2,3,2, respectively, which are all less than 4. A related concept is that of a largely composite number, a positive integer that has at least as many divisors as all smaller positive integers. The name can be somewhat misleading, as the first two highly composite numbers (1 and 2) are not actually composite numbers; however, all further terms are. Ramanujan wrote a paper on highly composite numbers in 1915. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Composite Number Cuisenaire Rods 10
Composite or compositing may refer to: Materials * Composite material, a material that is made from several different substances ** Metal matrix composite, composed of metal and other parts ** Cermet, a composite of ceramic and metallic materials ** Dental composite, a substance used to fill cavities in teeth ** Composite armor, a type of tank armor * Alloy, a mixture of a metal and another element * Mixture, the combination of several different substances without chemical reaction Mathematics * Composite number, a positive integer that has at least one factor other than one or itself Science * Composite particle, a particle which is made up of smaller particles * ''Compositae'' or "composite family" of flowering plants * Composite volcano, a layered conical volcano * Compositing, another name for superposed epoch analysis, a statistical method used to analyze time series involving multiple events Technology * Compositing, combining of visual elements from separate sources i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square-free Integer
In mathematics, a square-free integer (or squarefree integer) is an integer which is divisible by no square number other than 1. That is, its prime factorization has exactly one factor for each prime that appears in it. For example, is square-free, but is not, because 18 is divisible by . The smallest positive square-free numbers are Square-free factorization Every positive integer n can be factored in a unique way as n=\prod_^k q_i^i, where the q_i different from one are square-free integers that are pairwise coprime. This is called the ''square-free factorization'' of . To construct the square-free factorization, let n=\prod_^h p_j^ be the prime factorization of n, where the p_j are distinct prime numbers. Then the factors of the square-free factorization are defined as q_i=\prod_p_j. An integer is square-free if and only if q_i=1 for all i > 1. An integer greater than one is the kth power of another integer if and only if k is a divisor of all i such that q_i\neq 1. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Allyn And Bacon
Allyn & Bacon, founded in 1868, is a higher education textbook publisher in the areas of education, humanities and social sciences. It is an imprint of Pearson Education, the world's largest education publishing and technology company, which is part of Pearson PLC. Allyn & Bacon was an independent company until it was purchased by Esquire, Inc., the former publishers of the magazine of the same name, in 1981. Esquire, Inc. was sold to Gulf+Western in 1983, and Allyn & Bacon became part of Simon & Schuster Simon & Schuster LLC (, ) is an American publishing house owned by Kohlberg Kravis Roberts since 2023. It was founded in New York City in 1924, by Richard L. Simon and M. Lincoln Schuster. Along with Penguin Random House, Hachette Book Group US ...'s education division. Pearson purchased the education and reference divisions of Simon & Schuster in 1998. In 2007, Allyn & Bacon merged with Merrill, also a Pearson company. As a result of the merge, the company's website c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Blaisdell Publishing Company
Blaisdell is a surname. Notable people with the surname include: * Alfred Blaisdell, politician from North Dakota * Daniel Blaisdell, politician from New Hampshire * Frances Blaisdell, musician from New Jersey * Frank Ellsworth Blaisdell (1862–1946), American professor of surgery and entomologist * James A. Blaisdell, founder of the Claremont Colleges * John Blaisdell Corliss, politician from Michigan * Kealii Blaisdell, Kanaka Maoli activist and notable Hawaiian songwriter * Mike Blaisdell, Canadian ice hockey player * Neal Blaisdell, mayor of Honolulu ** Neal S. Blaisdell Center, multi-purpose center in Honolulu named after the mayor * Paul Blaisdell, American artist and special effects creator * Richard Kekuni Blaisdell, professor of medicine in Honolulu * Tex Blaisdell, American comics creator * William Blaisdell, American actor See also *'' Home Building & Loan Ass'n v. Blaisdell'', a United States Supreme Court decision upholding a state's mortgage modification law {{su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Addison-Wesley
Addison–Wesley is an American publisher of textbooks and computer literature. It is an imprint of Pearson plc, a global publishing and education company. In addition to publishing books, Addison–Wesley also distributes its technical titles through the O'Reilly Online Learning e-reference service. Addison–Wesley's majority of sales derive from the United States (55%) and Europe (22%). The Addison–Wesley Professional Imprint produces content including books, eBooks, and video for the professional IT worker including developers, programmers, managers, system administrators. Classic titles include '' The Art of Computer Programming'', '' The C++ Programming Language'', '' The Mythical Man-Month'', and '' Design Patterns''. History Lew Addison Cummings and Melbourne Wesley Cummings founded Addison–Wesley in 1942, with the first book published by Addison–Wesley being Massachusetts Institute of Technology professor Francis Weston Sears' ''Mechanics''. Its first comput ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Table Of Prime Factors
The tables contain the prime factorization of the natural numbers from 1 to 1000. When ''n'' is a prime number, the prime factorization is just ''n'' itself, written in bold below. The number 1 is called a unit. It has no prime factors and is neither prime nor composite. Properties Many properties of a natural number ''n'' can be seen or directly computed from the prime factorization of ''n''. *The multiplicity of a prime factor ''p'' of ''n'' is the largest exponent ''m'' for which ''pm'' divides ''n''. The tables show the multiplicity for each prime factor. If no exponent is written then the multiplicity is 1 (since ''p'' = ''p''1). The multiplicity of a prime which does not divide ''n'' may be called 0 or may be considered undefined. *Ω(''n''), the prime omega function, is the number of prime factors of ''n'' counted with multiplicity (so it is the sum of all prime factor multiplicities). *A prime number has Ω(''n'') = 1. The first: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 3 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
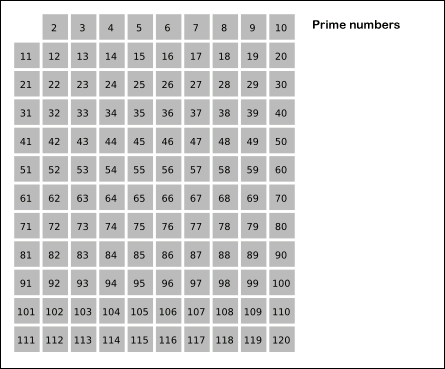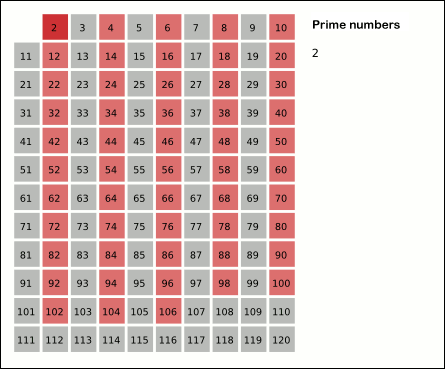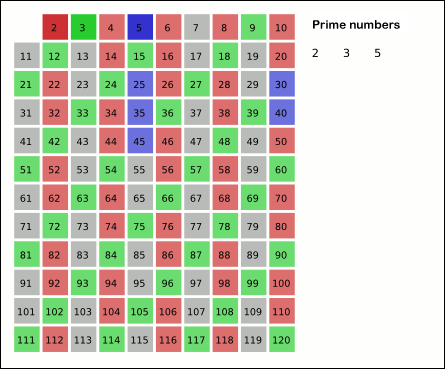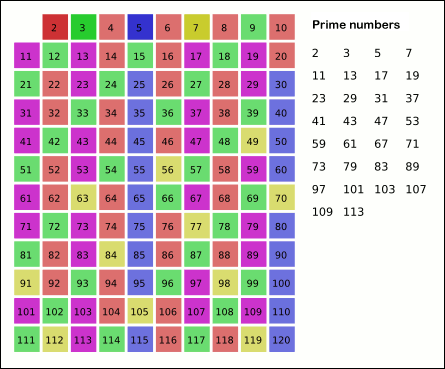
Sieve Of Eratosthenes
In mathematics, the sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to any given limit. It does so by iteratively marking as composite number, composite (i.e., not prime) the multiples of each prime, starting with the first prime number, 2. The multiples of a given prime are generated as a sequence of numbers starting from that prime, with arithmetic progression, constant difference between them that is equal to that prime.Horsley, Rev. Samuel, F. R. S., "' or, The Sieve of Eratosthenes. Being an account of his method of finding all the Prime Numbers,''Philosophical Transactions'' (1683–1775), Vol. 62. (1772), pp. 327–347 This is the sieve's key distinction from using trial division to sequentially test each candidate number for divisibility by each prime. Once all the multiples of each discovered prime have been marked as composites, the remaining unmarked numbers are primes. The earliest known reference to the sieve (, ''kóskinon Eratosthén ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer Factorization
In mathematics, integer factorization is the decomposition of a positive integer into a product of integers. Every positive integer greater than 1 is either the product of two or more integer factors greater than 1, in which case it is a composite number, or it is not, in which case it is a prime number. For example, is a composite number because , but is a prime number because it cannot be decomposed in this way. If one of the factors is composite, it can in turn be written as a product of smaller factors, for example . Continuing this process until every factor is prime is called prime factorization; the result is always unique up to the order of the factors by the prime factorization theorem. To factorize a small integer using mental or pen-and-paper arithmetic, the simplest method is trial division: checking if the number is divisible by prime numbers , , , and so on, up to the square root of . For larger numbers, especially when using a computer, various more sophis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Canonical Representation Of A Positive Integer
In mathematics, the fundamental theorem of arithmetic, also called the unique factorization theorem and prime factorization theorem, states that every integer greater than 1 is prime or can be represented uniquely as a product of prime numbers, up to the order of the factors. For example, : 1200 = 2^4 \cdot 3^1 \cdot 5^2 = (2 \cdot 2 \cdot 2 \cdot 2) \cdot 3 \cdot (5 \cdot 5) = 5 \cdot 2 \cdot 5 \cdot 2 \cdot 3 \cdot 2 \cdot 2 = \ldots The theorem says two things about this example: first, that 1200 be represented as a product of primes, and second, that no matter how this is done, there will always be exactly four 2s, one 3, two 5s, and no other primes in the product. The requirement that the factors be prime is necessary: factorizations containing composite numbers may not be unique (for example, 12 = 2 \cdot 6 = 3 \cdot 4). This theorem is one of the main reasons why 1 is not considered a prime number: if 1 were prime, then factorization into primes would not be unique; f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rough Number
A ''k''-rough number, as defined by Finch in 2001 and 2003, is a positive integer whose prime factors are all greater than or equal to ''k''. ''k''-roughness has alternately been defined as requiring all prime factors to strictly exceed ''k''.p. 130, Naccache and Shparlinski 2009. Examples (after Finch) #Every odd positive integer is 3-rough. #Every positive integer that is congruent to 1 or 5 mod 6 is 5-rough. #Every positive integer is 2-rough, since all its prime factors, being prime numbers, exceed 1. See also * Buchstab function, used to count rough numbers * Smooth number Notes References * Finch's definition from Number Theory Archives* "Divisibility, Smoothness and Cryptographic Applications", D. Naccache and I. E. Shparlinski, pp. 115–173 in ''Algebraic Aspects of Digital Communications'', eds. Tanush Shaska and Engjell Hasimaj, IOS Press, 2009, . The On-Line Encyclopedia of Integer Sequences The On-Line Encyclopedia of Integer Sequences (OEIS) is an online ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Smooth Number
In number theory, an ''n''-smooth (or ''n''-friable) number is an integer whose prime factors are all less than or equal to ''n''. For example, a 7-smooth number is a number in which every prime factor is at most 7. Therefore, 49 = 72 and 15750 = 2 × 32 × 53 × 7 are both 7-smooth, while 11 and 702 = 2 × 33 × 13 are not 7-smooth. The term seems to have been coined by Leonard Adleman. Smooth numbers are especially important in cryptography, which relies on factorization of integers. 2-smooth numbers are simply the Power of two, powers of 2, while 5-smooth numbers are also known as regular numbers. Definition A negative and positive numbers, positive integer is called B-smooth if none of its prime factors are greater than B. For example, 1,620 has prime factorization 22 × 34 × 5; therefore 1,620 is 5-smooth because none of its prime factors are greater than 5. This definition includes numbers that lack some of the smaller prime factors; for example, both 10 and 12 are 5-smooth, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |