Second-harmonic generation on:
[Wikipedia]
[Google]
[Amazon]
 Second-harmonic generation (SHG), also known as frequency doubling, is the lowest-order wave-wave nonlinear interaction that occurs in various systems, including optical, radio, atmospheric, and magnetohydrodynamic systems. As a prototype behavior of waves, SHG is widely used, for example, in doubling laser frequencies. SHG was initially discovered as a
Second-harmonic generation (SHG), also known as frequency doubling, is the lowest-order wave-wave nonlinear interaction that occurs in various systems, including optical, radio, atmospheric, and magnetohydrodynamic systems. As a prototype behavior of waves, SHG is widely used, for example, in doubling laser frequencies. SHG was initially discovered as a  Generating the second harmonic, often called frequency doubling, is also a process in radio communication; it was developed early in the 20th century and has been used with frequencies in the megahertz range. It is a special case of frequency multiplication.
Generating the second harmonic, often called frequency doubling, is also a process in radio communication; it was developed early in the 20th century and has been used with frequencies in the megahertz range. It is a special case of frequency multiplication.
 Second-harmonic generation was first demonstrated by Peter Franken, A. E. Hill, C. W. Peters, and G. Weinreich at the
Second-harmonic generation was first demonstrated by Peter Franken, A. E. Hill, C. W. Peters, and G. Weinreich at the
 Second-harmonic generation occurs in three types for critical phase-matching, denoted 0, I and II. In ''Type 0 SHG'' two photons having
Second-harmonic generation occurs in three types for critical phase-matching, denoted 0, I and II. In ''Type 0 SHG'' two photons having
 Early experiments in the field demonstrated second-harmonic generation from metal surfaces. Eventually, SHG was used to probe the air-water interface, allowing for detailed information about molecular orientation and ordering at one of the most ubiquitous of surfaces. It can be shown that the specific elements of :
:
where ''N''''s'' is the adsorbate density, ''θ'' is the angle that the molecular axis ''z'' makes with the surface normal ''Z'', and is the dominating element of the nonlinear polarizability of a molecule at an interface, allow one to determine ''θ'', given laboratory coordinates . Using an interference SHG method to determine these elements of ''χ''(2), the first molecular orientation measurement showed that the hydroxyl group of phenol pointed downwards into the water at the air-water interface (as expected due to the potential of hydroxyl groups to form hydrogen bonds). Additionally SHG at planar surfaces has revealed differences in ''pK''''a'' and rotational motions of molecules at interfaces.
Early experiments in the field demonstrated second-harmonic generation from metal surfaces. Eventually, SHG was used to probe the air-water interface, allowing for detailed information about molecular orientation and ordering at one of the most ubiquitous of surfaces. It can be shown that the specific elements of :
:
where ''N''''s'' is the adsorbate density, ''θ'' is the angle that the molecular axis ''z'' makes with the surface normal ''Z'', and is the dominating element of the nonlinear polarizability of a molecule at an interface, allow one to determine ''θ'', given laboratory coordinates . Using an interference SHG method to determine these elements of ''χ''(2), the first molecular orientation measurement showed that the hydroxyl group of phenol pointed downwards into the water at the air-water interface (as expected due to the potential of hydroxyl groups to form hydrogen bonds). Additionally SHG at planar surfaces has revealed differences in ''pK''''a'' and rotational motions of molecules at interfaces.
 Second-harmonic light can also be generated from surfaces that are "locally" planar, but may have inversion symmetry (centrosymmetric) on a larger scale. Specifically, recent theory has demonstrated that SHG from small spherical particles (micro- and nanometer scale) is allowed by proper treatment of Rayleigh scattering (scattering without a change in frequency from absorbed to emitted waves). At the surface of a small sphere, inversion symmetry is broken, allowing for SHG and other even order harmonics to occur.
For a colloidal system of microparticles at relatively low concentrations, the total SH signal , is given by:
:
where is the SH electric field generated by the ''j''th particle, and ''n'' the density of particles. The SH light generated from each particle is coherent, but adds incoherently to the SH light generated by others (as long as density is low enough). Thus, SH light is only generated from the interfaces of the spheres and their environment and is independent of particle-particle interactions. It has also been shown that the second-harmonic electric field scales with the radius of the particle cubed, a3.
Besides spheres, other small particles like rods have been studied similarly by SHG. Both immobilized and colloidal systems of small particles can be investigated. Recent experiments using second-harmonic generation of non-planar systems include transport kinetics across living cell membranes and demonstrations of SHG in complex nanomaterials.
Second-harmonic light can also be generated from surfaces that are "locally" planar, but may have inversion symmetry (centrosymmetric) on a larger scale. Specifically, recent theory has demonstrated that SHG from small spherical particles (micro- and nanometer scale) is allowed by proper treatment of Rayleigh scattering (scattering without a change in frequency from absorbed to emitted waves). At the surface of a small sphere, inversion symmetry is broken, allowing for SHG and other even order harmonics to occur.
For a colloidal system of microparticles at relatively low concentrations, the total SH signal , is given by:
:
where is the SH electric field generated by the ''j''th particle, and ''n'' the density of particles. The SH light generated from each particle is coherent, but adds incoherently to the SH light generated by others (as long as density is low enough). Thus, SH light is only generated from the interfaces of the spheres and their environment and is independent of particle-particle interactions. It has also been shown that the second-harmonic electric field scales with the radius of the particle cubed, a3.
Besides spheres, other small particles like rods have been studied similarly by SHG. Both immobilized and colloidal systems of small particles can be investigated. Recent experiments using second-harmonic generation of non-planar systems include transport kinetics across living cell membranes and demonstrations of SHG in complex nanomaterials.
 The SHG radiation pattern generated by an exciting Gaussian beam also has a (homogeneous) 2D Gaussian profile if the nonlinear medium being excited is homogeneous (A). However, if the exciting beam is positioned at an interface between opposite polarities (± boundary, ''B'') that is parallel to the beam propagation (see figure), the SHG will be split into two lobes whose amplitudes have opposite sign, i.e. are phase-shifted.
These boundaries can be found in the
The SHG radiation pattern generated by an exciting Gaussian beam also has a (homogeneous) 2D Gaussian profile if the nonlinear medium being excited is homogeneous (A). However, if the exciting beam is positioned at an interface between opposite polarities (± boundary, ''B'') that is parallel to the beam propagation (see figure), the SHG will be split into two lobes whose amplitudes have opposite sign, i.e. are phase-shifted.
These boundaries can be found in the 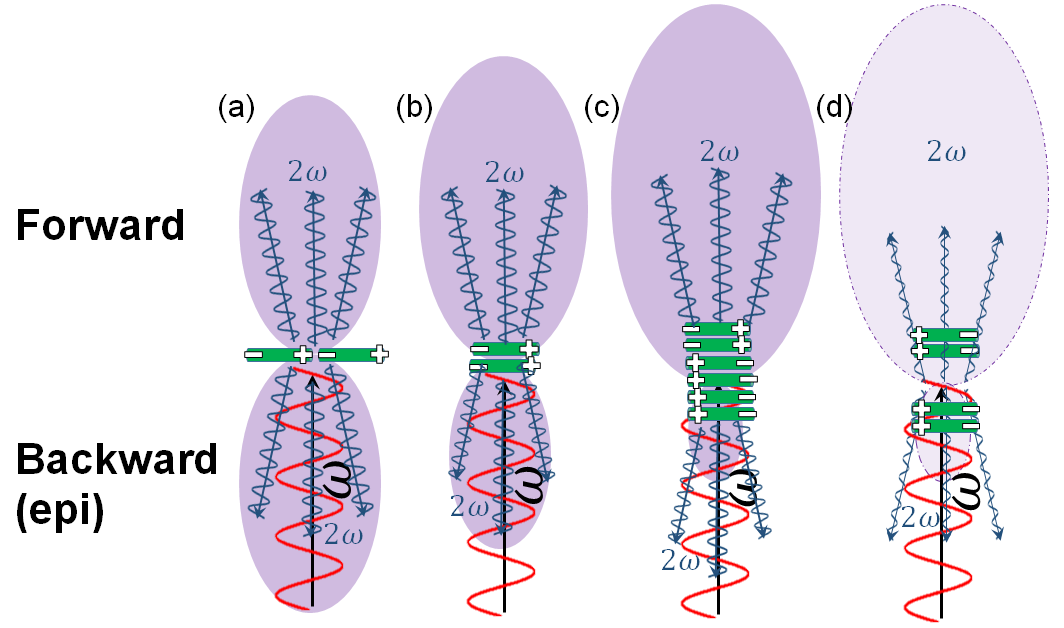 The forward (''F'') to backward (''B'') ratio is dependent on the arrangement of the different dipoles (green in figure) that are being excited. With only one dipole ((a) in the figure), ''F'' = ''B'', but ''F'' becomes higher than ''B'' when more dipoles are stacked along the propagation direction (b and c). However, the Gouy phase-shift of the Gaussian beam will imply a phase-shift between the SHGs generated at the edges of the focal volume, and can thus result in destructive interferences (zero signal) if there are dipoles at these edges having the same orientation (case (d) in the figure).
The forward (''F'') to backward (''B'') ratio is dependent on the arrangement of the different dipoles (green in figure) that are being excited. With only one dipole ((a) in the figure), ''F'' = ''B'', but ''F'' becomes higher than ''B'' when more dipoles are stacked along the propagation direction (b and c). However, the Gouy phase-shift of the Gaussian beam will imply a phase-shift between the SHGs generated at the edges of the focal volume, and can thus result in destructive interferences (zero signal) if there are dipoles at these edges having the same orientation (case (d) in the figure).

 When the conversion to 2nd harmonic becomes significant it becomes necessary to include depletion of the fundamental. The energy conversion states that all the involved fields verify the Manley–Rowe relations. One then has the coupled equations:
:
where denotes the complex conjugate. For simplicity, assume phase matched generation (). Then, energy conservation requires that
:
where is the complex conjugate of the other term, or
:
When the conversion to 2nd harmonic becomes significant it becomes necessary to include depletion of the fundamental. The energy conversion states that all the involved fields verify the Manley–Rowe relations. One then has the coupled equations:
:
where denotes the complex conjugate. For simplicity, assume phase matched generation (). Then, energy conservation requires that
:
where is the complex conjugate of the other term, or
:
 Now we solve the equations with the premise
:
and obtain
:
which leads to
:
Using
:
we get
:
If we assume a real , the relative phases for real harmonic growth must be such that . Then
:
or
:
where . From , it also follows that
:
Now we solve the equations with the premise
:
and obtain
:
which leads to
:
Using
:
we get
:
If we assume a real , the relative phases for real harmonic growth must be such that . Then
:
or
:
where . From , it also follows that
:
 Second-harmonic generation (SHG), also known as frequency doubling, is the lowest-order wave-wave nonlinear interaction that occurs in various systems, including optical, radio, atmospheric, and magnetohydrodynamic systems. As a prototype behavior of waves, SHG is widely used, for example, in doubling laser frequencies. SHG was initially discovered as a
Second-harmonic generation (SHG), also known as frequency doubling, is the lowest-order wave-wave nonlinear interaction that occurs in various systems, including optical, radio, atmospheric, and magnetohydrodynamic systems. As a prototype behavior of waves, SHG is widely used, for example, in doubling laser frequencies. SHG was initially discovered as a nonlinear optical
Nonlinear optics (NLO) is the branch of optics that describes the behaviour of light in nonlinear media, that is, media in which the polarization density P responds non-linearly to the electric field E of the light. The non-linearity is typicall ...
process in which two photon
A photon () is an elementary particle that is a quantum of the electromagnetic field, including electromagnetic radiation such as light and radio waves, and the force carrier for the electromagnetic force. Photons are massless particles that can ...
s with the same frequency interact with a nonlinear material, are "combined", and generate a new photon with twice the energy of the initial photons (equivalently, twice the frequency
Frequency is the number of occurrences of a repeating event per unit of time. Frequency is an important parameter used in science and engineering to specify the rate of oscillatory and vibratory phenomena, such as mechanical vibrations, audio ...
and half the wavelength
In physics and mathematics, wavelength or spatial period of a wave or periodic function is the distance over which the wave's shape repeats.
In other words, it is the distance between consecutive corresponding points of the same ''phase (waves ...
), that conserves the coherence of the excitation. It is a special case of sum-frequency generation (2 photons), and more generally of harmonic generation.
The second-order nonlinear susceptibility of a medium characterizes its tendency to cause SHG. Second-harmonic generation, like other even-order nonlinear optical phenomena, is not allowed in media with inversion symmetry (in the leading electric dipole contribution). However, effects such as the Bloch–Siegert shift (oscillation), found when two-level systems are driven at Rabi frequencies comparable to their transition frequencies, will give rise to second-harmonic generation in centro-symmetric systems. In addition, in non-centrosymmetric crystal
A crystal or crystalline solid is a solid material whose constituents (such as atoms, molecules, or ions) are arranged in a highly ordered microscopic structure, forming a crystal lattice that extends in all directions. In addition, macros ...
s belonging to crystallographic point group 432, SHG is not possible and under Kleinman's conditions SHG in 422 and 622 point groups should vanish, although some exceptions exist.
In some cases, almost 100% of the light energy can be converted to the second-harmonic frequency. These cases typically involve intense pulsed laser beams passing through large crystals and careful alignment to obtain phase matching
Nonlinear optics (NLO) is the branch of optics that describes the behaviour of light in nonlinear media, that is, media in which the polarization density P responds non-linearly to the electric field E of the light. The non-linearity is typicall ...
. In other cases, like second-harmonic imaging microscopy, only a tiny fraction of the light energy is converted to the second harmonic, but this light can nevertheless be detected with the help of optical filters.
 Generating the second harmonic, often called frequency doubling, is also a process in radio communication; it was developed early in the 20th century and has been used with frequencies in the megahertz range. It is a special case of frequency multiplication.
Generating the second harmonic, often called frequency doubling, is also a process in radio communication; it was developed early in the 20th century and has been used with frequencies in the megahertz range. It is a special case of frequency multiplication.
History
 Second-harmonic generation was first demonstrated by Peter Franken, A. E. Hill, C. W. Peters, and G. Weinreich at the
Second-harmonic generation was first demonstrated by Peter Franken, A. E. Hill, C. W. Peters, and G. Weinreich at the University of Michigan
The University of Michigan (U-M, U of M, or Michigan) is a public university, public research university in Ann Arbor, Michigan, United States. Founded in 1817, it is the oldest institution of higher education in the state. The University of Mi ...
, Ann Arbor, in 1961. The demonstration was made possible by the invention of the laser
A laser is a device that emits light through a process of optical amplification based on the stimulated emission of electromagnetic radiation. The word ''laser'' originated as an acronym for light amplification by stimulated emission of radi ...
, which created the required high-intensity coherent light. They focused a ruby laser with a wavelength of 694 nm into a quartz sample. They sent the output light through a spectrometer, recording the spectrum on photographic paper, which indicated the production of light at 347 nm. Famously, when published in the journal ''Physical Review Letters'', the copy editor mistook the dim spot (at 347 nm) on the photographic paper as a speck of dirt and removed it from the publication. The formulation of SHG was initially described by N. Bloembergen and P. S. Pershan at Harvard in 1962. In their extensive evaluation of Maxwell's equations
Maxwell's equations, or Maxwell–Heaviside equations, are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, Electrical network, electr ...
at the planar interface between a linear and nonlinear medium, several rules for the interaction of light in non-linear media were elucidated.
Types in crystals
Critical phase-matching
 Second-harmonic generation occurs in three types for critical phase-matching, denoted 0, I and II. In ''Type 0 SHG'' two photons having
Second-harmonic generation occurs in three types for critical phase-matching, denoted 0, I and II. In ''Type 0 SHG'' two photons having extraordinary polarization
Birefringence, also called double refraction, is the optical property of a material having a refractive index that depends on the polarization and propagation direction of light. These optically anisotropic materials are described as birefrin ...
with respect to the crystal will combine to form a single photon with double the frequency/energy and extraordinary polarization. In ''Type I SHG'' two photons having ordinary polarization
Birefringence, also called double refraction, is the optical properties, optical property of a material having a refractive index that depends on the polarization (waves), polarization and propagation direction of light. These optically anisotro ...
with respect to the crystal will combine to form one photon with double the frequency and extraordinary polarization. In ''Type II SHG'', two photons having orthogonal polarizations will combine to form one photon with double the frequency and ordinary polarization. For a given crystal orientation, only one of these types of SHG occurs. In general to utilise ''Type 0'' interactions a quasi-phase-matching crystal type will be required, for example periodically poled lithium niobate (PPLN).
Non-critical phase-matching
Since phase-matching process basically means to match the optical indices at ω and 2ω, it can also be done by a temperature control in some birefringent crystals, because n changes with the temperature. For instance, LBO presents a perfect phase-matching at 25 °C for a SHG excited at 1200 or 1400 nm, but needs to be elevated at 200 °C for SHG with the usual laser line of 1064 nm. It is called "non-critical" because it does not depend on the crystal orientation as usual phase-matching.Surface second-harmonic generation
Since media with inversion symmetry are forbidden from generating second-harmonic light via the leading-order electric dipole contribution (unlike third harmonic generation), surfaces and interfaces make interesting subjects for study with SHG. In fact, second-harmonic generation and sum frequency generation discriminate against signals from the bulk, implicitly labeling them as surface specific techniques. In 1982, T. F. Heinz and Y. R. Shen explicitly demonstrated for the first time that SHG could be used as a spectroscopic technique to probe molecular monolayers adsorbed to surfaces. Heinz and Shen adsorbed monolayers of laser dye rhodamine to a planar fused silica surface; the coated surface was then pumped by a nanosecond ultra-fast laser. SH light with characteristic spectra of the adsorbed molecule and its electronic transitions were measured as reflection from the surface and demonstrated a quadratic power dependence on the pump laser power. In SHG surface spectroscopy, one focuses on measuring twice the incident frequency 2''ω'' given an incoming electric field in order to reveal information about a surface. Simply (for a more in-depth derivation see below), the induced second-harmonic dipole per unit volume, , can be written as : where is known as the nonlinear susceptibility tensor and is a characteristic to the materials at the interface of study. The generated and corresponding have been shown to reveal information about the orientation of molecules at a surface/interface, the interfacial analytical chemistry of surfaces, and chemical reactions at interfaces.From planar surfaces
 Early experiments in the field demonstrated second-harmonic generation from metal surfaces. Eventually, SHG was used to probe the air-water interface, allowing for detailed information about molecular orientation and ordering at one of the most ubiquitous of surfaces. It can be shown that the specific elements of :
:
where ''N''''s'' is the adsorbate density, ''θ'' is the angle that the molecular axis ''z'' makes with the surface normal ''Z'', and is the dominating element of the nonlinear polarizability of a molecule at an interface, allow one to determine ''θ'', given laboratory coordinates . Using an interference SHG method to determine these elements of ''χ''(2), the first molecular orientation measurement showed that the hydroxyl group of phenol pointed downwards into the water at the air-water interface (as expected due to the potential of hydroxyl groups to form hydrogen bonds). Additionally SHG at planar surfaces has revealed differences in ''pK''''a'' and rotational motions of molecules at interfaces.
Early experiments in the field demonstrated second-harmonic generation from metal surfaces. Eventually, SHG was used to probe the air-water interface, allowing for detailed information about molecular orientation and ordering at one of the most ubiquitous of surfaces. It can be shown that the specific elements of :
:
where ''N''''s'' is the adsorbate density, ''θ'' is the angle that the molecular axis ''z'' makes with the surface normal ''Z'', and is the dominating element of the nonlinear polarizability of a molecule at an interface, allow one to determine ''θ'', given laboratory coordinates . Using an interference SHG method to determine these elements of ''χ''(2), the first molecular orientation measurement showed that the hydroxyl group of phenol pointed downwards into the water at the air-water interface (as expected due to the potential of hydroxyl groups to form hydrogen bonds). Additionally SHG at planar surfaces has revealed differences in ''pK''''a'' and rotational motions of molecules at interfaces.
From non-planar surfaces
 Second-harmonic light can also be generated from surfaces that are "locally" planar, but may have inversion symmetry (centrosymmetric) on a larger scale. Specifically, recent theory has demonstrated that SHG from small spherical particles (micro- and nanometer scale) is allowed by proper treatment of Rayleigh scattering (scattering without a change in frequency from absorbed to emitted waves). At the surface of a small sphere, inversion symmetry is broken, allowing for SHG and other even order harmonics to occur.
For a colloidal system of microparticles at relatively low concentrations, the total SH signal , is given by:
:
where is the SH electric field generated by the ''j''th particle, and ''n'' the density of particles. The SH light generated from each particle is coherent, but adds incoherently to the SH light generated by others (as long as density is low enough). Thus, SH light is only generated from the interfaces of the spheres and their environment and is independent of particle-particle interactions. It has also been shown that the second-harmonic electric field scales with the radius of the particle cubed, a3.
Besides spheres, other small particles like rods have been studied similarly by SHG. Both immobilized and colloidal systems of small particles can be investigated. Recent experiments using second-harmonic generation of non-planar systems include transport kinetics across living cell membranes and demonstrations of SHG in complex nanomaterials.
Second-harmonic light can also be generated from surfaces that are "locally" planar, but may have inversion symmetry (centrosymmetric) on a larger scale. Specifically, recent theory has demonstrated that SHG from small spherical particles (micro- and nanometer scale) is allowed by proper treatment of Rayleigh scattering (scattering without a change in frequency from absorbed to emitted waves). At the surface of a small sphere, inversion symmetry is broken, allowing for SHG and other even order harmonics to occur.
For a colloidal system of microparticles at relatively low concentrations, the total SH signal , is given by:
:
where is the SH electric field generated by the ''j''th particle, and ''n'' the density of particles. The SH light generated from each particle is coherent, but adds incoherently to the SH light generated by others (as long as density is low enough). Thus, SH light is only generated from the interfaces of the spheres and their environment and is independent of particle-particle interactions. It has also been shown that the second-harmonic electric field scales with the radius of the particle cubed, a3.
Besides spheres, other small particles like rods have been studied similarly by SHG. Both immobilized and colloidal systems of small particles can be investigated. Recent experiments using second-harmonic generation of non-planar systems include transport kinetics across living cell membranes and demonstrations of SHG in complex nanomaterials.
Radiation pattern
 The SHG radiation pattern generated by an exciting Gaussian beam also has a (homogeneous) 2D Gaussian profile if the nonlinear medium being excited is homogeneous (A). However, if the exciting beam is positioned at an interface between opposite polarities (± boundary, ''B'') that is parallel to the beam propagation (see figure), the SHG will be split into two lobes whose amplitudes have opposite sign, i.e. are phase-shifted.
These boundaries can be found in the
The SHG radiation pattern generated by an exciting Gaussian beam also has a (homogeneous) 2D Gaussian profile if the nonlinear medium being excited is homogeneous (A). However, if the exciting beam is positioned at an interface between opposite polarities (± boundary, ''B'') that is parallel to the beam propagation (see figure), the SHG will be split into two lobes whose amplitudes have opposite sign, i.e. are phase-shifted.
These boundaries can be found in the sarcomere
A sarcomere (Greek σάρξ ''sarx'' "flesh", μέρος ''meros'' "part") is the smallest functional unit of striated muscle tissue. It is the repeating unit between two Z-lines. Skeletal striated muscle, Skeletal muscles are composed of tubular ...
s of muscle
Muscle is a soft tissue, one of the four basic types of animal tissue. There are three types of muscle tissue in vertebrates: skeletal muscle, cardiac muscle, and smooth muscle. Muscle tissue gives skeletal muscles the ability to muscle contra ...
s (protein = myosin
Myosins () are a Protein family, family of motor proteins (though most often protein complexes) best known for their roles in muscle contraction and in a wide range of other motility processes in eukaryotes. They are adenosine triphosphate, ATP- ...
), for instance. Note that we have considered here only the forward generation.
Moreover the SHG phase-matching can also result in : some SHG is also emitted in backward (epi direction). When the phase-matching is not fulfilled, as in biological tissue
In biology, tissue is an assembly of similar cells and their extracellular matrix from the same embryonic origin that together carry out a specific function. Tissues occupy a biological organizational level between cells and a complete or ...
s, the backward signal comes from a sufficiently high phase-mismatch which allow a small backward contribution to compensate for it. Unlike fluorescence, the spatial coherence of the process constrain it to emit only in those two directions, where the coherence length in the backwards direction is always much smaller than in the forwards, meaning there is always more forward than backward SHG signal.
 The forward (''F'') to backward (''B'') ratio is dependent on the arrangement of the different dipoles (green in figure) that are being excited. With only one dipole ((a) in the figure), ''F'' = ''B'', but ''F'' becomes higher than ''B'' when more dipoles are stacked along the propagation direction (b and c). However, the Gouy phase-shift of the Gaussian beam will imply a phase-shift between the SHGs generated at the edges of the focal volume, and can thus result in destructive interferences (zero signal) if there are dipoles at these edges having the same orientation (case (d) in the figure).
The forward (''F'') to backward (''B'') ratio is dependent on the arrangement of the different dipoles (green in figure) that are being excited. With only one dipole ((a) in the figure), ''F'' = ''B'', but ''F'' becomes higher than ''B'' when more dipoles are stacked along the propagation direction (b and c). However, the Gouy phase-shift of the Gaussian beam will imply a phase-shift between the SHGs generated at the edges of the focal volume, and can thus result in destructive interferences (zero signal) if there are dipoles at these edges having the same orientation (case (d) in the figure).
Applications
Green lasers
Second-harmonic generation is used by the laser industry to make green 532 nm lasers from a 1064 nm source. The 1064 nm light is fed through a bulk nonlinear crystal (typically made of KDP or KTP). In high-quality diode lasers the crystal is coated on the output side with an infrared filter to prevent leakage of intense 1064 nm or 808 nm infrared light into the beam. Both of these wavelengths are invisible and do not trigger the defensive "blink-reflex" reaction in the eye and can therefore be a special hazard to human eyes. Furthermore, some laser safety eyewear intended for argon or other green lasers may filter out the green component (giving a false sense of safety), but transmit the infrared. Nevertheless, some "greenlaser pointer
A laser pointer or laser pen is a (typically battery-powered) handheld device that uses a laser diode to emit a narrow low-power visible laser beam (i.e. Coherence (physics), coherent light) to highlight something of interest with a small brigh ...
" products have become available on the market which omit the expensive infrared filter, often without warning.
Ultra-short pulse measurement
Second-harmonic generation is also used for measuring ultra-short pulse widths with autocorrelators. Characterizing an ultrashort pulse (like measuring its temporal width) cannot be done directly with electronics only, as the time-scale is below 1ps (sec) : it needs to use the pulse itself, that is why an autocorrelation function is often used. SHG has the advantage of mixing two input fields to generate the harmonic one, it is thus a good candidate (but not the only one) to perform such a pulse measurement. Optical autocorrelation, in its intensity or fringe-resolved ( interferometric) version use SHG, unlike field autocorrelation. Also, most versions of theFROG
A frog is any member of a diverse and largely semiaquatic group of short-bodied, tailless amphibian vertebrates composing the order (biology), order Anura (coming from the Ancient Greek , literally 'without tail'). Frog species with rough ski ...
(called SHG-FROG) use SHG to mix the delayed fields.
Second-harmonic generation microscopy
In biological and medical science, the effect of second-harmonic generation is used for high-resolution optical microscopy. Because of the non-zero second-harmonic coefficient, only non-centrosymmetric structures are capable of emitting SHG light. One such structure is collagen, which is found in most load-bearing tissues. Using a short-pulse laser such as a femtosecond laser and a set of appropriate filters the excitation light can be easily separated from the emitted, frequency-doubled SHG signal. This allows for very high axial and lateral resolution comparable to that ofconfocal microscopy
Confocal microscopy, most frequently confocal laser scanning microscopy (CLSM) or laser scanning confocal microscopy (LSCM), is an optical imaging technique for increasing optical resolution and contrast (vision), contrast of a micrograph by me ...
without having to use pinholes. SHG microscopy has been used for studies of the cornea
The cornea is the transparency (optics), transparent front part of the eyeball which covers the Iris (anatomy), iris, pupil, and Anterior chamber of eyeball, anterior chamber. Along with the anterior chamber and Lens (anatomy), lens, the cornea ...
and lamina cribrosa sclerae, both of which consist primarily of collagen. Second-harmonic generation can be produced by several non-centrosymmetric organic dyes; however, most of the organic dyes also generate collateral fluorescence along with second-harmonic generation signals. Until now, only two classes of organic dyes have been shown which do not produce any collateral fluorescence and works purely on second-harmonic generation. Recently, using two-photon excited fluorescence and second-harmonic generation-based microscopy, a group of Oxford University researchers showed that organic porphyrin-type molecules can have different transition dipole moments for two-photon fluorescence and second-harmonic generation, which are otherwise thought to occur from the same transition dipole moment.
Second-harmonic generation microscopy is also used in material science, for instance to characterize nanostructured materials.
Characterization of crystalline materials
Second harmonic generation is also relevant to characterize organic or inorganic crystals since is one of the most discriminant and rapid technique to detect non-centrosymmetry. In addition, this technique can be used on single crystal as well as on powdered samples. One should recall that SHG is only possible (from the bulk) in non-centrosymmetric (NC)crystal
A crystal or crystalline solid is a solid material whose constituents (such as atoms, molecules, or ions) are arranged in a highly ordered microscopic structure, forming a crystal lattice that extends in all directions. In addition, macros ...
s. The part of non-centroysmmetric crystals in nature is much lower than centrosymmetric crystals (circa 22% of the Cambridge structural database), but the frequency of NC crystals increases by a lot in pharmaceutical, biological and electronic fields because of the particular properties of these crystals ( piezoelectricity, pyroelectricity, polar phases, chirality, etc.).
In 1968 (7 years after the first experimental evidence of SHG on single crystal), Kurtz and Perry started to develop a SHG analyzer to rapidly detect the presence or not of inversion center in powdered crystalline samples. The detection of a SHG signal has been shown to be reliable and sensitive test for the detection of crystalline non-centrosymmetry with the confidence level higher than 99%. It is a relevant tool to resolve space group ambiguities that can arise from Friedel's law in single-crystal X-ray diffraction. Furthermore, the method is referenced in the International Tables for Crystallography and is described as a "powerful method of testing crystalline materials for the absence of a symmetry center."
One possible application is also to rapidly discriminate chiral phases such as conglomerate that are of particular interest for pharmaceutical industries. It could also be used as a technique to probe the structural purity of material if one of the impurities is NC reaching a detection threshold as low as 1 ppm using Kurtz–Perry apparatus up to one part in 10 billion by volume using a SHG microscope.
Due to the high sensitivity of the technique, it can be a helpful tool in the accurate determination of phase diagram and can also be used to monitor phase transitions ( polymorphic transition, dehydration, ...) when at least one of the phases is NC.
Theoretical derivation (plane wave)
At low conversion
The simplest case for analysis of second-harmonic generation is a plane wave of amplitude ''E''(''ω'') traveling in a nonlinear medium in the direction of its ''k'' vector. A polarization is generated at the second-harmonic frequency: : where is the effective nonlinear optical coefficient which is dependent on specific components of that are involved in this particular interaction. The wave equation at 2ω (assuming negligible loss and asserting the slowly varying envelope approximation) is : where . At low conversion efficiency (''E''(2''ω'') ≪ ''E''(''ω'')) the amplitude remains essentially constant over the interaction length, . Then, with the boundary condition we obtain : In terms of the optical intensity, , this is, : This intensity is maximized for the phase-matched condition Δ''k'' = 0. If the process is not phase matched, the driving polarization at ''ω'' goes in and out of phase with generated wave ''E''(2''ω'') and conversion oscillates as sin(Δ''kℓ''/2). The coherence length is defined as . It does not pay to use a nonlinear crystal much longer than the coherence length. ( Periodic poling and quasi-phase-matching provide another approach to this problem.)With depletion

 When the conversion to 2nd harmonic becomes significant it becomes necessary to include depletion of the fundamental. The energy conversion states that all the involved fields verify the Manley–Rowe relations. One then has the coupled equations:
:
where denotes the complex conjugate. For simplicity, assume phase matched generation (). Then, energy conservation requires that
:
where is the complex conjugate of the other term, or
:
When the conversion to 2nd harmonic becomes significant it becomes necessary to include depletion of the fundamental. The energy conversion states that all the involved fields verify the Manley–Rowe relations. One then has the coupled equations:
:
where denotes the complex conjugate. For simplicity, assume phase matched generation (). Then, energy conservation requires that
:
where is the complex conjugate of the other term, or
:
 Now we solve the equations with the premise
:
and obtain
:
which leads to
:
Using
:
we get
:
If we assume a real , the relative phases for real harmonic growth must be such that . Then
:
or
:
where . From , it also follows that
:
Now we solve the equations with the premise
:
and obtain
:
which leads to
:
Using
:
we get
:
If we assume a real , the relative phases for real harmonic growth must be such that . Then
:
or
:
where . From , it also follows that
:
Theoretical expression with Gaussian beams
The excitation wave is assumed to be a Gaussian beam, of amplitude: with , the direction of propagation, the Rayleigh range, thewave vector
In physics, a wave vector (or wavevector) is a vector used in describing a wave, with a typical unit being cycle per metre. It has a magnitude and direction. Its magnitude is the wavenumber of the wave (inversely proportional to the wavelength) ...
.
Each wave verifies the wave equation
:
where .
With phase-matching
It can be shown that: (a Gaussian), is a solution of the equation (''n'' = 2 for SHG).No phase-matching
A non-perfect phase-matching is a more realistic condition in practice, especially in biological samples. The paraxial approximation is however supposed still valid: , and in the harmonic expression, is now . In the special case of SHG (''n'' = 2), in a medium of length ''L'' and a focus position , the intensity writes: : where is thespeed of light
The speed of light in vacuum, commonly denoted , is a universal physical constant exactly equal to ). It is exact because, by international agreement, a metre is defined as the length of the path travelled by light in vacuum during a time i ...
in vacuum
A vacuum (: vacuums or vacua) is space devoid of matter. The word is derived from the Latin adjective (neuter ) meaning "vacant" or "void". An approximation to such vacuum is a region with a gaseous pressure much less than atmospheric pressur ...
, the vacuum permittivity
In electromagnetism, the absolute permittivity, often simply called permittivity and denoted by the Greek letter (epsilon), is a measure of the electric polarizability of a dielectric material. A material with high permittivity polarizes more ...
, the optical index of the medium at and the waist size of excitation.
Thus, the SHG intensity quickly decays in the bulk (), due to the Gouy phase-shift of the Gaussian beam.
In conformity with experiments, the SHG signal vanishes in the bulk (if the medium thickness is too large), and the SHG must be generated at the surface of the material: the conversion therefore does not strictly scales with the square of the number of scatterers, contrary to what the plane wave model indicates. Interestingly, the signal also vanishes in bulk for higher orders, like THG.
Materials used
Materials capable of generating a second harmonic are crystals without inversion symmetry, except crystals with point group 432. This eliminates water and glass. Notably, filamentous biological proteins with a cylindrical symmetric such ascollagen
Collagen () is the main structural protein in the extracellular matrix of the connective tissues of many animals. It is the most abundant protein in mammals, making up 25% to 35% of protein content. Amino acids are bound together to form a trip ...
, tubulin or myosin
Myosins () are a Protein family, family of motor proteins (though most often protein complexes) best known for their roles in muscle contraction and in a wide range of other motility processes in eukaryotes. They are adenosine triphosphate, ATP- ...
, but also certain carbohydrates
A carbohydrate () is a biomolecule composed of carbon (C), hydrogen (H), and oxygen (O) atoms. The typical hydrogen-to-oxygen atomic ratio is 2:1, analogous to that of water, and is represented by the empirical formula (where ''m'' and ''n'' ma ...
(such as starch
Starch or amylum is a polymeric carbohydrate consisting of numerous glucose units joined by glycosidic bonds. This polysaccharide is produced by most green plants for energy storage. Worldwide, it is the most common carbohydrate in human diet ...
or cellulose
Cellulose is an organic compound with the chemical formula, formula , a polysaccharide consisting of a linear chain of several hundred to many thousands of glycosidic bond, β(1→4) linked glucose, D-glucose units. Cellulose is an important s ...
) are also quite good converters of SHG (fundamental in the near infrared).
Examples of crystal
A crystal or crystalline solid is a solid material whose constituents (such as atoms, molecules, or ions) are arranged in a highly ordered microscopic structure, forming a crystal lattice that extends in all directions. In addition, macros ...
s used with for SHG conversion:
* Fundamental excitation at 600–1500 nm: BiBO (BiB3O6)
* Fundamental excitation at 570–4000 nm: lithium iodate LiIO3.
* Fundamental excitation at 800–1100 nm, often 860 or 980 nm: potassium niobate KNbO3.
* Fundamental excitation at 410–2000 nm: BBO (β-BaB2O4).
* Fundamental excitation at 984–3400 nm: KTP (KTiOPO4) or KTA.
* Fundamental excitation at ~1000–2000 nm: periodically poled crystals, like PPLN.
For common types of diode-pumped solid state lasers with input wavelengths:
* 1064 nm: monopotassium phosphate KDP (KH2PO4), lithium triborate (LiB3O5), CsLiB6O10 and barium borate BBO(β-BaB2O4).
* 1319 nm: KNbO3, BBO (β-BaB2O4), monopotassium phosphate KDP (KH2PO4), LiIO3, LiNbO3, and potassium titanyl phosphate
Potassium titanyl phosphate (KTP) is an inorganic compound with the formula . It is a white solid. KTP is an important nonlinear optics, nonlinear optical material that is commonly used for second-harmonic generation, frequency-doubling diode-pum ...
KTP (KTiOPO4).
See also
* Half-harmonic generation * Harmonic generation *Nonlinear optics
Nonlinear optics (NLO) is the branch of optics that describes the behaviour of light in Nonlinearity, nonlinear media, that is, media in which the polarization density P responds non-linearly to the electric field E of the light. The non-linearity ...
* Optical frequency multiplier
* Second-harmonic imaging microscopy
* Spontaneous parametric down-conversion
* Surface second harmonic generation
References
External links
Articles
* * {{DEFAULTSORT:Second-Harmonic Generation Second harmonic generation