|
Gaussian Beam
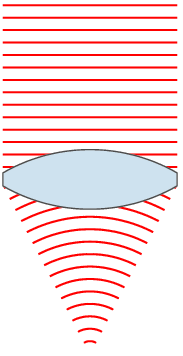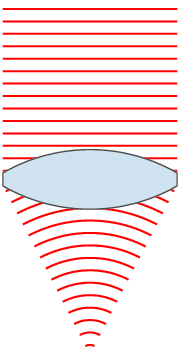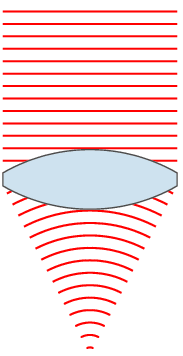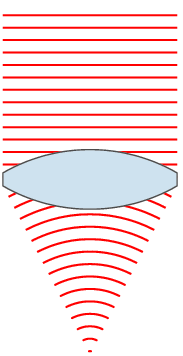
In optics, a Gaussian beam is an idealized beam of electromagnetic radiation whose amplitude envelope in the transverse plane is given by a Gaussian function; this also implies a Gaussian intensity (irradiance) profile. This fundamental (or TEM00) transverse Gaussian mode describes the intended output of many lasers, as such a beam diverges less and can be focused better than any other. When a Gaussian beam is refocused by an ideal lens, a new Gaussian beam is produced. The electric and magnetic field amplitude profiles along a circular Gaussian beam of a given wavelength and polarization are determined by two parameters: the waist , which is a measure of the width of the beam at its narrowest point, and the position relative to the waist.Svelto, pp. 153–5. Since the Gaussian function is infinite in extent, perfect Gaussian beams do not exist in nature, and the edges of any such beam would be cut off by any finite lens or mirror. However, the Gaussian is a useful appro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gaussian Beam W40mm Lambda30mm
Carl Friedrich Gauss (1777–1855) is the eponym of all of the topics listed below. There are over 100 topics all named after this German mathematician and scientist, all in the fields of mathematics, physics, and astronomy. The English eponymous adjective ''Gaussian'' is pronounced . Mathematics Algebra and linear algebra Geometry and differential geometry Number theory Cyclotomic fields *Gaussian period *Gaussian rational *Gauss sum, an exponential sum over Dirichlet characters **Elliptic Gauss sum, an analog of a Gauss sum **Quadratic Gauss sum Analysis, numerical analysis, vector calculus and calculus of variations Complex analysis and convex analysis *Gauss–Lucas theorem *Gauss's continued fraction, an analytic continued fraction derived from the hypergeometric functions *Gauss's test, Gauss's criterion – described oEncyclopedia of Mathematics*Gauss's hypergeometric theorem, an identity on hypergeometric series *Gauss plane Statistics *Gaus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Helmholtz Equation
In mathematics, the Helmholtz equation is the eigenvalue problem for the Laplace operator. It corresponds to the elliptic partial differential equation: \nabla^2 f = -k^2 f, where is the Laplace operator, is the eigenvalue, and is the (eigen)function. When the equation is applied to waves, is known as the wave number. The Helmholtz equation has a variety of applications in physics and other sciences, including the wave equation, the diffusion equation, and the Schrödinger equation for a free particle. In optics, the Helmholtz equation is the wave equation for the electric field. The equation is named after Hermann von Helmholtz, who studied it in 1860. from the Encyclopedia of Mathematics. Motivation and uses The Helmholtz equation often arises in the study of physical problems involving par ...[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Frequency
In physics, angular frequency (symbol ''ω''), also called angular speed and angular rate, is a scalar measure of the angle rate (the angle per unit time) or the temporal rate of change of the phase argument of a sinusoidal waveform or sine function (for example, in oscillations and waves). Angular frequency (or angular speed) is the magnitude of the pseudovector quantity '' angular velocity''. (UP1) Angular frequency can be obtained multiplying '' rotational frequency'', ''ν'' (or ordinary ''frequency'', ''f'') by a full turn (2 radians): . It can also be formulated as , the instantaneous rate of change of the angular displacement, ''θ'', with respect to time, ''t''. (11 pages) Unit In SI[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Velocity
The phase velocity of a wave is the rate at which the wave propagates in any medium. This is the velocity at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave (for example, the crest) will appear to travel at the phase velocity. The phase velocity is given in terms of the wavelength (lambda) and time period as :v_\mathrm = \frac. Equivalently, in terms of the wave's angular frequency , which specifies angular change per unit of time, and wavenumber (or angular wave number) , which represent the angular change per unit of space, :v_\mathrm = \frac. To gain some basic intuition for this equation, we consider a propagating (cosine) wave . We want to see how fast a particular phase of the wave travels. For example, we can choose , the phase of the first crest. This implies , and so . Formally, we let the phase and see immediately that and . So, it immediately follows that : \frac = -\frac \frac = \frac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gouy Phase
In optics, a Gaussian beam is an idealized beam of electromagnetic radiation whose amplitude envelope in the transverse plane is given by a Gaussian function; this also implies a Gaussian intensity (irradiance) profile. This fundamental (or TEM00) transverse Gaussian mode describes the intended output of many lasers, as such a beam diverges less and can be focused better than any other. When a Gaussian beam is refocused by an ideal lens, a new Gaussian beam is produced. The electric and magnetic field amplitude profiles along a circular Gaussian beam of a given wavelength and polarization are determined by two parameters: the waist , which is a measure of the width of the beam at its narrowest point, and the position relative to the waist.Svelto, pp. 153–5. Since the Gaussian function is infinite in extent, perfect Gaussian beams do not exist in nature, and the edges of any such beam would be cut off by any finite lens or mirror. However, the Gaussian is a useful app ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wavefront
In physics, the wavefront of a time-varying ''wave field (physics), field'' is the set (locus (mathematics), locus) of all point (geometry), points having the same ''phase (waves), phase''. The term is generally meaningful only for fields that, at each point, vary sinusoidally in time with a single temporal frequency (otherwise the phase is not well defined). Wavefronts usually move with time. For waves propagating in a dimension (mathematics), unidimensional medium, the wavefronts are usually single points; they are curves in a two dimensional medium, and surface (mathematics), surfaces in a three-dimensional one. For a sinusoidal plane wave, the wavefronts are planes perpendicular to the direction of propagation, that move in that direction together with the wave. For a sinusoidal spherical wave, the wavefronts are spherical surfaces that expand with it. If the speed of propagation is different at different points of a wavefront, the shape and/or orientation of the wavefro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wavefront Curvature
In physics, the wavefront of a time-varying ''wave field'' is the set ( locus) of all points having the same ''phase''. The term is generally meaningful only for fields that, at each point, vary sinusoidally in time with a single temporal frequency (otherwise the phase is not well defined). Wavefronts usually move with time. For waves propagating in a unidimensional medium, the wavefronts are usually single points; they are curves in a two dimensional medium, and surfaces in a three-dimensional one. For a sinusoidal plane wave, the wavefronts are planes perpendicular to the direction of propagation, that move in that direction together with the wave. For a sinusoidal spherical wave, the wavefronts are spherical surfaces that expand with it. If the speed of propagation is different at different points of a wavefront, the shape and/or orientation of the wavefronts may change by refraction. In particular, lenses can change the shape of optical wavefronts from planar to sphe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. It is defined such that one radian is the angle subtended at the centre of a circle by an Circular arc, arc that is equal in length to the radius. The unit was formerly an SI supplementary unit and is currently a dimensionless unit, dimensionless SI derived unit,: "The CGPM decided to interpret the supplementary units in the SI, namely the radian and the steradian, as dimensionless derived units." defined in the SI as 1 rad = 1 and expressed in terms of the SI base unit metre (m) as . Angles without explicitly specified units are generally assumed to be measured in radians, especially in mathematical writing. Definition One radian is defined as the angle at the center of a circle in a plane that wikt:subtend, subtends an arc whose length equals the radius of the circle. More generally, the magnit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave Number
In the physical sciences, the wavenumber (or wave number), also known as repetency, is the spatial frequency of a wave. Ordinary wavenumber is defined as the number of wave cycles divided by length; it is a physical quantity with dimension of reciprocal length, expressed in SI units of cycles per metre or reciprocal metre (m−1). Angular wavenumber, defined as the wave phase divided by time, is a quantity with dimension of angle per length and SI units of radians per metre. They are analogous to temporal frequency, respectively the '' ordinary frequency'', defined as the number of wave cycles divided by time (in cycles per second or reciprocal seconds), and the ''angular frequency'', defined as the phase angle divided by time (in radians per second). In multidimensional systems, the wavenumber is the magnitude of the ''wave vector''. The space of wave vectors is called ''reciprocal space''. Wave numbers and wave vectors play an essential role in optics and the physics of w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Imaginary Unit
The imaginary unit or unit imaginary number () is a mathematical constant that is a solution to the quadratic equation Although there is no real number with this property, can be used to extend the real numbers to what are called complex numbers, using addition and multiplication. A simple example of the use of in a complex number is Imaginary numbers are an important mathematical concept; they extend the real number system \mathbb to the complex number system \mathbb, in which at least one Root of a function, root for every nonconstant polynomial exists (see Algebraic closure and Fundamental theorem of algebra). Here, the term ''imaginary'' is used because there is no real number having a negative square (algebra), square. There are two complex square roots of and , just as there are two complex square roots of every real number other than zero (which has one multiple root, double square root). In contexts in which use of the letter is ambiguous or problematic, the le ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phasor
In physics and engineering, a phasor (a portmanteau of phase vector) is a complex number representing a sinusoidal function whose amplitude and initial phase are time-invariant and whose angular frequency is fixed. It is related to a more general concept called analytic representation,Bracewell, Ron. ''The Fourier Transform and Its Applications''. McGraw-Hill, 1965. p269 which decomposes a sinusoid into the product of a complex constant and a factor depending on time and frequency. The complex constant, which depends on amplitude and phase, is known as a phasor, or complex amplitude, and (in older texts) sinor or even complexor. A common application is in the steady-state analysis of an electrical network powered by time varying current where all signals are assumed to be sinusoidal with a common frequency. Phasor representation allows the analyst to represent the amplitude and phase of the signal using a single complex number. The only difference in their analytic rep ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transverse Electromagnetic Mode
A transverse mode of electromagnetic radiation is a particular electromagnetic field pattern of the radiation in the plane perpendicular (i.e., transverse) to the radiation's propagation direction. Transverse modes occur in radio waves and microwaves confined to a waveguide, and also in light waves in an optical fiber and in a laser's optical resonator. Transverse modes occur because of boundary conditions imposed on the wave by the waveguide. For example, a radio wave in a hollow metal waveguide must have zero tangential electric field amplitude at the walls of the waveguide, so the transverse pattern of the electric field of waves is restricted to those that fit between the walls. For this reason, the modes supported by a waveguide are quantized. The allowed modes can be found by solving Maxwell's equations for the boundary conditions of a given waveguide. Types of modes Unguided electromagnetic waves in free space, or in a bulk isotropic dielectric, can be described as a sup ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |