Roulette (curve)

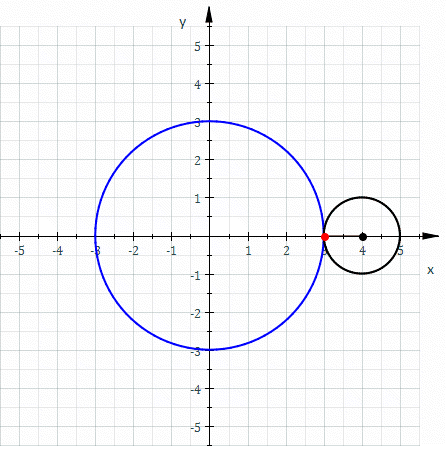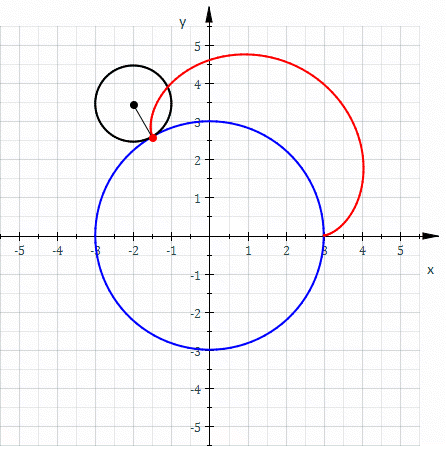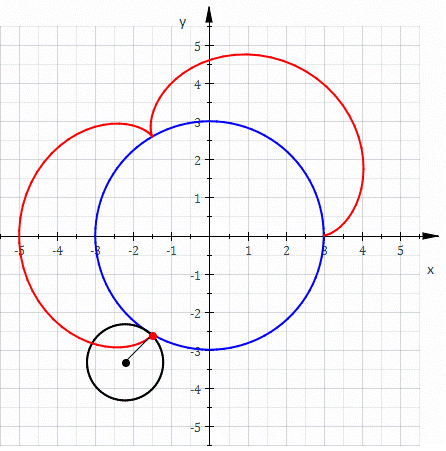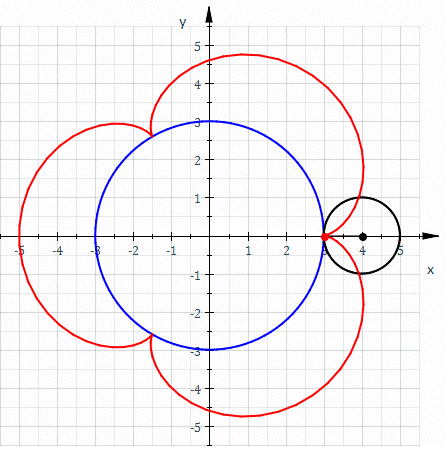In the differential geometry of curves, a roulette is a kind of curve, generalizing cycloids, epicycloids, hypocycloids, trochoids, epitrochoids, hypotrochoids, and involutes. On a basic level, it is the path traced by a curve while rolling on another curve without slipping.

Definition

Informal definition

Roughly speaking, a roulette is the curve described by a point (called the ''generator'' or ''pole'') attached to a given curve as that curve rolls without slipping, along a second given curve that is fixed. More precisely, given a curve attached to a plane which is moving so that the curve rolls, without slipping, along a given curve attached to a fixed plane occupying the same space, then a point attached to the moving plane describes a curve, in the fixed plane called a roulette.

Special cases and related concepts

In the case where the rolling curve is a line and the generator is a point on the line, the roulette is called an involute of the fixed curve. If the rolling curve is a circle and the fixed curve is a line then the roulette is a trochoid. If, in this case, the point lies on the circle then the roulette is a cycloid.

A related concept is a glissette, the curve described by a point attached to a given curve as it slides along two (or more) given curves.

Formal definition

Formally speaking, the curves must be differentiable curves in the Euclidean plane. The ''fixed curve'' is kept invariant; the ''rolling curve'' is subjected to a continuous congruence transformation such that at all times the curves are tangent at a point of contact that moves with the same speed when taken along either curve (another way to express this constraint is that the point of contact of the two curves is the instant centre of rotation of the congruence transformation). The resulting roulette is formed by the locus of the generator subjected to the same set of congruence transformations.

Modeling the original curves as curves in the complex plane, let $r,f:\mathbb R\to\Complex$ be the two natural parameterizations of the rolling ( and fixed curves, such that $r(0)=f(0)$, $r'(0) = f'(0)$, and $, r'(t), = , f'(t), \neq 0$ for all $t$. The roulette of generator $p\in\Complex$ as $r$ is rolled on $f$ is then given by the mapping:

:$t\mapsto f(t)+(p-r(t)) .$

Generalizations

If, instead of a single point being attached to the rolling curve, another given curve is carried along the moving plane, a family of congruent curves is produced. The envelope of this family may also be called a roulette.

Roulettes in higher spaces can certainly be imagined but one needs to align more than just the tangents.

Example

If the fixed curve is a catenary and the rolling curve is a line, we have:

:$f(t)=t+i(\cosh(t)-1) \qquad r(t)=\sinh(t)$

:$f'(t)=1+i\sinh(t) \qquad r'(t)=\cosh(t).$

The parameterization of the line is chosen so that
:$, f'(t), = \sqrt = \sqrt = , r'(t), .$

Applying the formula above we obtain:

:$f(t)+(p-r(t)) =t-i+ =t-i+(p+i).$

If ''p'' = −''i'' the expression has a constant imaginary part (namely −''i'') and the roulette is a horizontal line. An interesting application of this is that a square wheel could roll without bouncing on a road that is a matched series of catenary arcs.

List of roulettes

See also

* Rolling
* Gear
* Locus (mathematics)
* Superposition principle
* Spirograph
* Tusi couple
* Rosetta (orbit)

Notes

References

* W. H. Besant (1890)
Notes on Roulettes and Glissettes
' from Cornell University Historical Math Monographs, originally published by Deighton, Bell & Co.
*

Further reading

Roulette at 2dcurves.comBase, roulante et roulettes d'un mouvement plan sur plan

{{Authority control