|
Cycloid
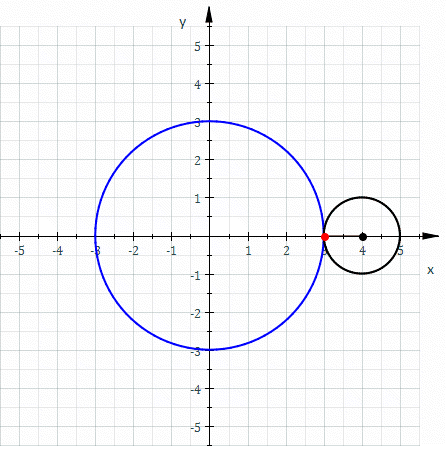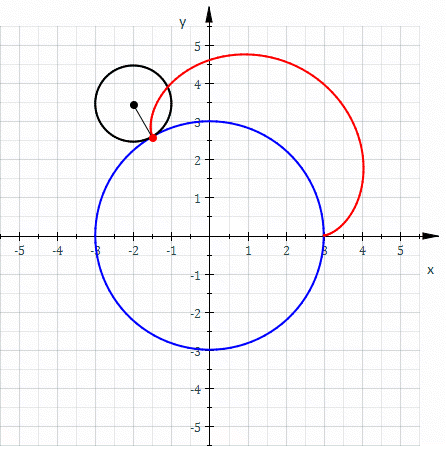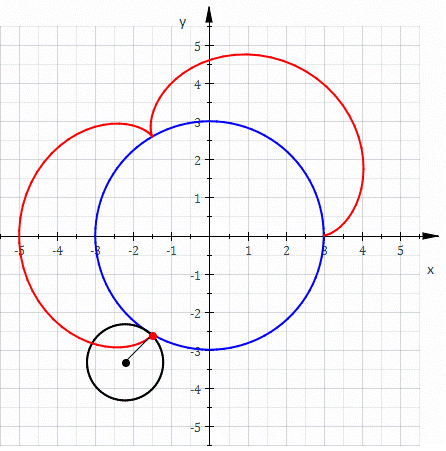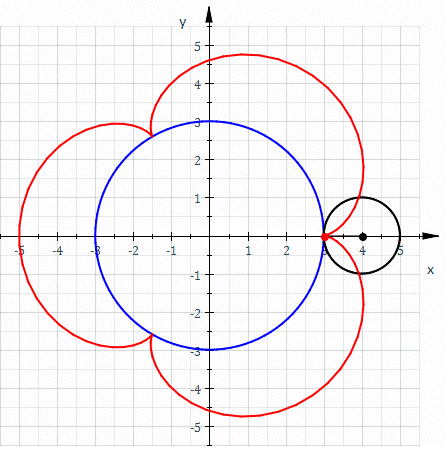
In geometry, a cycloid is the curve traced by a point on a circle as it Rolling, rolls along a Line (geometry), straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette (curve), roulette, a curve generated by a curve rolling on another curve. The cycloid, with the Cusp (singularity), cusps pointing upward, is the curve of fastest descent under uniform gravity (the brachistochrone curve). It is also the form of a curve for which the Frequency, period of an object in simple harmonic motion (rolling up and down repetitively) along the curve does not depend on the object's starting position (the tautochrone curve). In physics, when a charged particle at rest is put under a uniform Electric field, electric and magnetic field perpendicular to one another, the particle’s trajectory draws out a cycloid. History The cycloid has been called "The Helen of Geometers" as, like Helen of Troy, it caused frequent quarrels among 17th-centur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cycloid F
In geometry, a cycloid is the curve In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight. Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that ... traced by a point on a circle as it Rolling, rolls along a Line (geometry), straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette (curve), roulette, a curve generated by a curve rolling on another curve. The cycloid, with the Cusp (singularity), cusps pointing upward, is the curve of fastest descent under uniform gravity (the brachistochrone curve). It is also the form of a curve for which the Frequency, period of an object in simple harmonic motion (rolling up and down repetitively) along the curve does not depend on the object's starting position (the tautochrone curve). In physics, when a charged particle at rest is put under a uniform Electr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
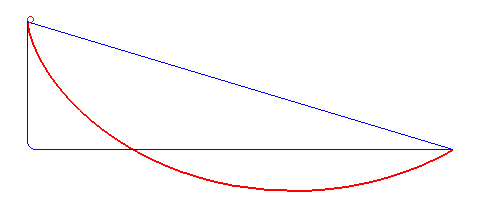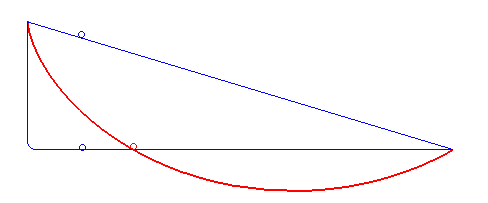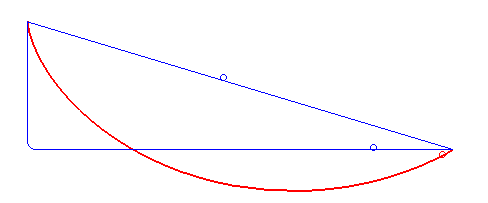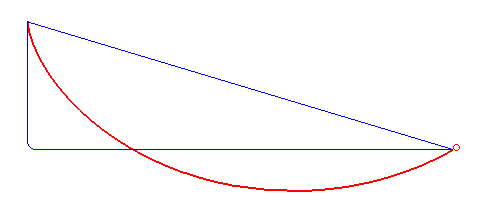
Brachistochrone Curve
In physics and mathematics, a brachistochrone curve (), or curve of fastest descent, is the one lying on the plane between a point ''A'' and a lower point ''B'', where ''B'' is not directly below ''A'', on which a bead slides frictionlessly under the influence of a uniform gravitational field to a given end point in the shortest time. The problem was posed by Johann Bernoulli in 1696 and solved by Isaac Newton in 1697. The brachistochrone curve is the same shape as the tautochrone curve; both are cycloids. However, the portion of the cycloid used for each of the two varies. More specifically, the brachistochrone can use up to a complete rotation of the cycloid (at the limit when A and B are at the same level), but always starts at a cusp. In contrast, the tautochrone problem can use only up to the first half rotation, and always ends at the horizontal.Stewart, James. "Section 10.1 - Curves Defined by Parametric Equations." ''Calculus: Early Transcendentals''. 7th ed. Belmont, CA: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tautochrone Curve
A tautochrone curve or isochrone curve () is the curve for which the time taken by an object sliding without friction in uniform gravity to its lowest point is independent of its starting point on the curve. The curve is a cycloid, and the time is equal to Pi, π times the square root of the radius of the circle which generates the cycloid, over the Gravitational acceleration, acceleration of gravity. The tautochrone curve is related to the brachistochrone curve, which is also a cycloid. The tautochrone problem The tautochrone problem, the attempt to identify this curve, was solved by Christiaan Huygens in 1659. He proved geometrically in his ''Horologium Oscillatorium'', originally published in 1673, that the curve is a cycloid. The cycloid is given by a point on a circle of radius r tracing a curve as the circle rolls along the x axis, as: \begin x &= r(\theta - \sin \theta) \\ y &= r(1 - \cos \theta), \end Huygens also proved that the time of descent is equal to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trochoid
In geometry, a trochoid () is a roulette curve formed by a circle rolling along a line. It is the curve traced out by a point fixed to a circle (where the point may be on, inside, or outside the circle) as it rolls along a straight line. If the point is on the circle, the trochoid is called ''common'' (also known as a cycloid); if the point is inside the circle, the trochoid is ''curtate''; and if the point is outside the circle, the trochoid is ''prolate''. The word "trochoid" was coined by Gilles de Roberval, referring to the special case of a cycloid. Basic description As a circle of radius rolls without slipping along a line , the center moves parallel to , and every other point in the rotating plane rigidly attached to the circle traces the curve called the trochoid. Let . Parametric equations of the trochoid for which is the -axis are :\begin & x = a\theta - b \sin \theta \\ & y = a - b \cos \theta \end where is the variable angle through which the circle rolls. C ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Roulette (curve)
In the differential geometry of curves, a roulette is a kind of curve, generalizing cycloids, epicycloids, hypocycloids, trochoids, epitrochoids, hypotrochoids, and involutes. On a basic level, it is the path traced by a curve while rolling on another curve without slipping. Definition Informal definition Roughly speaking, a roulette is the curve described by a point (called the ''generator'' or ''pole'') attached to a given curve as that curve rolls without slipping, along a second given curve that is fixed. More precisely, given a curve attached to a plane which is moving so that the curve rolls, without slipping, along a given curve attached to a fixed plane occupying the same space, then a point attached to the moving plane describes a curve, in the fixed plane called a roulette. Special cases and related concepts In the case where the rolling curve is a line and the generator is a point on the line, the roulette is called an involute of the fixed curve. If the rol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John Wallis
John Wallis (; ; ) was an English clergyman and mathematician, who is given partial credit for the development of infinitesimal calculus. Between 1643 and 1689 Wallis served as chief cryptographer for Parliament and, later, the royal court. He is credited with introducing the symbol ∞ to represent the concept of infinity. He similarly used 1/∞ for an infinitesimal. He was a contemporary of Newton and one of the greatest intellectuals of the early renaissance of mathematics. Biography Educational background * Cambridge, M.A., Oxford, D.D. * Grammar School at Tenterden, Kent, 1625–31. * School of Martin Holbeach at Felsted, Essex, 1631–2. * Cambridge University, Emmanuel College, 1632–40; B.A., 1637; M.A., 1640. * D.D. at Oxford in 1654. Family On 14 March 1645, he married Susanna Glynde ( – 16 March 1687). They had three children: # Anne, Lady Blencowe (4 June 1656 – 5 April 1718), married Sir John Blencowe (30 November 1642 – 6 May 1726) in 1675, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is called the radius. The length of a line segment connecting two points on the circle and passing through the centre is called the diameter. A circle bounds a region of the plane called a Disk (mathematics), disc. The circle has been known since before the beginning of recorded history. Natural circles are common, such as the full moon or a slice of round fruit. The circle is the basis for the wheel, which, with related inventions such as gears, makes much of modern machinery possible. In mathematics, the study of the circle has helped inspire the development of geometry, astronomy and calculus. Terminology * Annulus (mathematics), Annulus: a ring-shaped object, the region bounded by two concentric circles. * Circular arc, Arc: any Connected ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Curve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight. Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that appeared more than 2000 years ago in Euclid's ''Elements'': "The urvedline is ��the first species of quantity, which has only one dimension, namely length, without any width nor depth, and is nothing else than the flow or run of the point which ��will leave from its imaginary moving some vestige in length, exempt of any width." This definition of a curve has been formalized in modern mathematics as: ''A curve is the image of an interval to a topological space by a continuous function''. In some contexts, the function that defines the curve is called a ''parametrization'', and the curve is a parametric curve. In this article, these curves are sometimes called ''topological curves'' to distinguish them from more constrained curves su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rolling
Rolling is a Motion (physics)#Types of motion, type of motion that combines rotation (commonly, of an Axial symmetry, axially symmetric object) and Translation (geometry), translation of that object with respect to a surface (either one or the other moves), such that, if ideal conditions exist, the two are in contact with each other without sliding (motion), sliding. Rolling where there is no sliding is referred to as ''pure rolling''. By definition, there is no sliding when there is a frame of reference in which all points of contact on the rolling object have the same velocity as their counterparts on the surface on which the object rolls; in particular, for a frame of reference in which the rolling plane is at rest (see animation), the instantaneous velocity of all the points of contact (for instance, a generating line segment of a cylinder) of the rolling object is zero. In practice, due to small deformations near the contact area, some sliding and energy dissipation occurs. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sarah B
Sara Beth Bareilles ( ; born December 7, 1979) is an American singer, songwriter, musician, and actress. She has sold over three million albums and over 15 million singles in the United States. Bareilles has earned various accolades, including two Grammy Awards, as well as nominations for four Primetime Emmy Awards and three Tony Awards. In 2012, VH1 named her one of the Top 100 Greatest Women in Music. After signing with Epic Records, Bareilles rose to prominence with the release of her second studio album and major label debut, '' Little Voice'' (2007). Its lead single, " Love Song", peaked at number four on the ''Billboard'' Hot 100 and earned nominations for Song of the Year and Best Female Pop Vocal Performance at the 51st Annual Grammy Awards. Bareilles made her Broadway debut when she composed music and wrote lyrics for the 2015 musical '' Waitress'', for which she earned nominations for the Tony Award for Best Original Score and the Grammy Award for Best Musi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moritz Cantor
Moritz Benedikt Cantor (23 August 1829 – 10 April 1920) was a German historian of mathematics. Biography Cantor was born at Mannheim. He came from a Sephardi Jewish family that had emigrated to the Netherlands from Portugal, another branch of which had established itself in Russia. In his early youth, Moritz Cantor was not strong enough to go to school, and his parents decided to educate him at home. Later, however, he was admitted to an advanced class of the Gymnasium in Mannheim. From there he went to the University of Heidelberg in 1848, and soon after to the University of Göttingen, where he studied under Gauss and Weber, and where Stern awakened in him a strong interest in historical research. After obtaining his PhD at the University of Heidelberg in 1851, he went to Berlin, where he eagerly followed the lectures of Peter Gustav Lejeune Dirichlet; and upon his return to Heidelberg in 1853, he was appointed privat-docent at the university. In 1863, he was promoted ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |