resonant ultrasound spectroscopy on:
[Wikipedia]
[Google]
[Amazon]
Resonant ultrasound spectroscopy (RUS) is a laboratory technique used in
 Here, is the ith component of the
Here, is the ith component of the
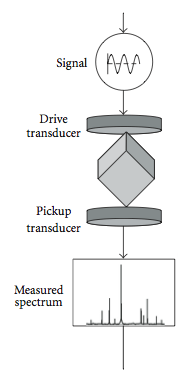 The most common method for detecting the mechanical resonant spectrum is illustrated in Fig. 2, where a small
The most common method for detecting the mechanical resonant spectrum is illustrated in Fig. 2, where a small
 Since the accuracy of the measure depends strictly on the accuracy in the sample preparation, several precautions are taken: RPRs are prepared with the edges parallel to crystallographic directions; for cylinders only the axis can be matched to sample
Since the accuracy of the measure depends strictly on the accuracy in the sample preparation, several precautions are taken: RPRs are prepared with the edges parallel to crystallographic directions; for cylinders only the axis can be matched to sample
geology
Geology (). is a branch of natural science concerned with the Earth and other astronomical objects, the rocks of which they are composed, and the processes by which they change over time. Modern geology significantly overlaps all other Earth ...
and material science
A material is a substance or mixture of substances that constitutes an object. Materials can be pure or impure, living or non-living matter. Materials can be classified on the basis of their physical and chemical properties, or on their geol ...
to measure fundamental material properties involving elasticity. This technique relies on the fact that solid objects have natural frequencies at which they vibrate when mechanically excited. The natural frequency depends on the elasticity, size, and shape of the object—RUS exploits this property of solids to determine the elastic tensor of the material. The great advantage of this technique is that the entire elastic tensor is obtained from a single crystal
In materials science, a single crystal (or single-crystal solid or monocrystalline solid) is a material in which the crystal lattice of the entire sample is continuous and unbroken to the edges of the sample, with no Grain boundary, grain bound ...
sample in a single rapid measurement. At lower or more general frequencies, this method is known as acoustic resonance spectroscopy.
History
Interest in elastic properties made its entrance with 17th century philosophers, but the real theory of elasticity, indicating that the elastic constants of a material could be obtained by measuring sound velocities in that material, was summarized only two hundred of years later. In 1964, D. B. Frasier and R. C. LeCraw used the solution calculated in 1880 by G. Lamé and H. Lamb to solve the forward problem, and then inverted it graphically, in what may be the first RUS measurement. Nevertheless, we had to wait for the participation of geophysics community, interested in determining the Earth's interior structure, to solve theinverse problem
An inverse problem in science is the process of calculating from a set of observations the causal factors that produced them: for example, calculating an image in X-ray computed tomography, sound source reconstruction, source reconstruction in ac ...
: in 1970 three geophysicists improved the previous method and introduced the term resonant sphere technique (RST). Excited by the encouraging results achieved with lunar samples, one of them gave one of his students the task of extending the method for use with cube shaped samples. This method, now known as the rectangular parallelepiped resonance (RPR) method, was further extended by I. Ohno in 1976. Finally, at the end of the 1980s, A. Migliori and J. Maynard expanded the limits of the technique in terms of loading and low-level electronic measurements, and with W. Visscher brought the computer algorithms to their current state, introducing the final term resonant ultrasound spectroscopy (RUS).
Theory
Firstly, one must solve the problem of calculating the natural frequencies in terms of sample dimensions, mass, and a set of hypothetical elastic constants (the forward problem). Then one must apply a nonlinear inversion algorithm to find the elastic constants from the measured natural frequencies (theinverse problem
An inverse problem in science is the process of calculating from a set of observations the causal factors that produced them: for example, calculating an image in X-ray computed tomography, sound source reconstruction, source reconstruction in ac ...
).
Lagrangian minimization
All RUS measurements are performed on samples that are free vibrators. Because a completeanalytical solution
In mathematics, an expression or equation is in closed form if it is formed with constants, variables, and a set of functions considered as ''basic'' and connected by arithmetic operations (, and integer powers) and function composition. C ...
for the free vibrations of solids does not exist, one must rely upon approximations. Finite element methods are based on balancing the forces applied to a differential volume element
In mathematics, a volume element provides a means for integrating a function with respect to volume in various coordinate systems such as spherical coordinates and cylindrical coordinates. Thus a volume element is an expression of the form
\ma ...
, then calculating its response. Energy minimization methods on the other hand determine the minimum energy, and thus the equilibrium configuration for the object. Among the energy minimization techniques, the Lagrangian minimization is the most used in the RUS analyses because of its advantage in speed (an order of magnitude smaller than the finite-element methods).
The procedure begins with an object of volume V, bounded by its free surface
In physics, a free surface is the surface of a fluid that is subject to zero parallel shear stress,
such as the interface between two homogeneous fluids.
An example of two such homogeneous fluids would be a body of water (liquid) and the air in ...
S. The Lagrangian is given by
where KE is the kinetic energy
In physics, the kinetic energy of an object is the form of energy that it possesses due to its motion.
In classical mechanics, the kinetic energy of a non-rotating object of mass ''m'' traveling at a speed ''v'' is \fracmv^2.Resnick, Rober ...
density
and PE is the potential energy
In physics, potential energy is the energy of an object or system due to the body's position relative to other objects, or the configuration of its particles. The energy is equal to the work done against any restoring forces, such as gravity ...
density
 Here, is the ith component of the
Here, is the ith component of the displacement vector
In geometry and mechanics, a displacement is a vector whose length is the shortest distance from the initial to the final position of a point P undergoing motion. It quantifies both the distance and direction of the net or total motion along ...
, ω is the angular frequency
In physics, angular frequency (symbol ''ω''), also called angular speed and angular rate, is a scalar measure of the angle rate (the angle per unit time) or the temporal rate of change of the phase argument of a sinusoidal waveform or sine ...
from harmonic time dependence, is a component of the elastic stiffness tensor, and ρ is the density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be u ...
. Subscripts i, j, etc., refer to Cartesian coordinate
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular o ...
directions.
To find the minimum of the Lagrangian, calculate the differential of L as a function of u, the arbitrary variation of u in V and on S. This gives:
Because is arbitrary in V and on S, both terms in square brackets must be zero. Setting the first term equal to zero yields the elastic wave equation. The second square bracketed term is an expression of free surface
In physics, a free surface is the surface of a fluid that is subject to zero parallel shear stress,
such as the interface between two homogeneous fluids.
An example of two such homogeneous fluids would be a body of water (liquid) and the air in ...
boundary conditions; is the unit vector normal to S. For a free body (as we assume it), the latter term sums to zero and can be ignored.
Thus the set of that satisfies the previously mentioned conditions are those displacements that correspond to ω being a normal mode
A normal mode of a dynamical system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The free motion described by the normal modes takes place at fixed frequencies ...
frequency of the system. This suggests that the normal vibrations of an object (Fig. 1) may be calculated by applying a variational method (in our case the Rayleigh-Ritz variational method, explained in the next paragraph) to determine both the normal mode frequencies and the description of the physical oscillations. To quote Visscher, getting both equations from the basic Lagrangian is "a mathematical fortuity that may have occurred during a lapse in Murphy's vigilance".
Rayleigh-Ritz variational method
The actuation of this approach requires the expansion of the in a set of basis functions appropriate to the geometry of the body, substituting that expression into Eq. (1) and reducing the problem to that of diagonalizing a N×N matrix (eigenvalue
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by a ...
problem). The stationary points of the Lagrangian are found by solving the eigenvalue problem resulting from Eq. (4), that is,
where an are the approximations to the motion expanded in a complete basis set, E comes from the kinetic energy
In physics, the kinetic energy of an object is the form of energy that it possesses due to its motion.
In classical mechanics, the kinetic energy of a non-rotating object of mass ''m'' traveling at a speed ''v'' is \fracmv^2.Resnick, Rober ...
term, and Γ comes from the elastic energy
Elastic energy is the mechanical potential energy stored in the configuration of a material or physical system as it is subjected to elastic deformation by work performed upon it. Elastic energy occurs when objects are impermanently compressed ...
term. The order of the matrices is ~10^3 for good approximations.
Equation (5) determines the resonance
Resonance is a phenomenon that occurs when an object or system is subjected to an external force or vibration whose frequency matches a resonant frequency (or resonance frequency) of the system, defined as a frequency that generates a maximu ...
frequencies from the elastic moduli.
The inverse problem
Theinverse problem
An inverse problem in science is the process of calculating from a set of observations the causal factors that produced them: for example, calculating an image in X-ray computed tomography, sound source reconstruction, source reconstruction in ac ...
of deducing the elastic constants from a measured spectrum
A spectrum (: spectra or spectrums) is a set of related ideas, objects, or properties whose features overlap such that they blend to form a continuum. The word ''spectrum'' was first used scientifically in optics to describe the rainbow of co ...
of mechanical resonance
Mechanical resonance is the tendency of a mechanical system to respond at greater amplitude when the frequency of its oscillations matches the system's natural frequency of vibration (its '' resonance frequency'' or ''resonant frequency'') clos ...
s has no analytical solution
In mathematics, an expression or equation is in closed form if it is formed with constants, variables, and a set of functions considered as ''basic'' and connected by arithmetic operations (, and integer powers) and function composition. C ...
, so it needs to be solved by computational methods. For the indirect method, a starting resonant frequency spectrum, (n=1,2,...) is calculated using estimated values for the elastic constants and the known sample dimensions and density. The difference between the calculated and measured resonance frequency spectrum, (n=1,2,...) is quantified by a figure of merit
A figure of merit (FOM) is a performance metric that characterizes the performance of a device, system, or method, relative to its alternatives. Examples
*Absolute alcohol content per currency unit in an alcoholic beverage
*accurizing, Accuracy o ...
function,
where (n=1,2,...) are weight coefficients reflecting the confidence on individual resonance measurements. Then, a minimization of the function F is sought by regressing the values of all the elastic constants using computer software
Software consists of computer programs that instruct the Execution (computing), execution of a computer. Software also includes design documents and specifications.
The history of software is closely tied to the development of digital comput ...
developed for this process.
Measurements
 The most common method for detecting the mechanical resonant spectrum is illustrated in Fig. 2, where a small
The most common method for detecting the mechanical resonant spectrum is illustrated in Fig. 2, where a small parallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms (the term ''rhomboid'' is also sometimes used with this meaning). By analogy, it relates to a parallelogram just as a cube relates to a square.
Three equiva ...
-shaped sample is lightly held between two piezoelectric transducers. One transducer is used to generate an elastic wave of constant amplitude
The amplitude of a periodic variable is a measure of its change in a single period (such as time or spatial period). The amplitude of a non-periodic signal is its magnitude compared with a reference value. There are various definitions of am ...
and varying frequency
Frequency is the number of occurrences of a repeating event per unit of time. Frequency is an important parameter used in science and engineering to specify the rate of oscillatory and vibratory phenomena, such as mechanical vibrations, audio ...
, whereas the other is used to detect the sample's resonance. As a frequency range is swept, a sequence of resonance
Resonance is a phenomenon that occurs when an object or system is subjected to an external force or vibration whose frequency matches a resonant frequency (or resonance frequency) of the system, defined as a frequency that generates a maximu ...
peaks is recorded. The position of these peaks occurs at the natural frequencies (from which the elastic constants are determined) and the quality factor
In physics and engineering, the quality factor or factor is a dimensionless parameter that describes how underdamped an oscillator or resonator is. It is defined as the ratio of the initial energy stored in the resonator to the energy lost in ...
Q (a measure of how narrow the resonance is) provides information about the dissipation
In thermodynamics, dissipation is the result of an irreversible process that affects a thermodynamic system. In a dissipative process, energy ( internal, bulk flow kinetic, or system potential) transforms from an initial form to a final form, wh ...
of elastic energy
Elastic energy is the mechanical potential energy stored in the configuration of a material or physical system as it is subjected to elastic deformation by work performed upon it. Elastic energy occurs when objects are impermanently compressed ...
.
Unlike in a conventional ultrasonic measure, in a method that resonates the sample a strong coupling between the transducer
A transducer is a device that Energy transformation, converts energy from one form to another. Usually a transducer converts a signal in one form of energy to a signal in another.
Transducers are often employed at the boundaries of automation, M ...
and the sample is not required, because the sample behaves as a natural amplifier
An amplifier, electronic amplifier or (informally) amp is an electronic device that can increase the magnitude of a signal (a time-varying voltage or current). It is a two-port electronic circuit that uses electric power from a power su ...
. Rather, keeping at minimum the couple between them, you get a good approximation to free surface
In physics, a free surface is the surface of a fluid that is subject to zero parallel shear stress,
such as the interface between two homogeneous fluids.
An example of two such homogeneous fluids would be a body of water (liquid) and the air in ...
boundary conditions and tend to preserve the Q, too.
For variable-temperature measurements the sample is held between the ends of two buffer rods that link the sample to the transducers (Fig. 3) because the transducers must be kept at room temperature
Room temperature, colloquially, denotes the range of air temperatures most people find comfortable indoors while dressed in typical clothing. Comfortable temperatures can be extended beyond this range depending on humidity, air circulation, and ...
. In terms of pressure
Pressure (symbol: ''p'' or ''P'') is the force applied perpendicular to the surface of an object per unit area over which that force is distributed. Gauge pressure (also spelled ''gage'' pressure)The preferred spelling varies by country and eve ...
, on the contrary, there is a limit of only a few bars, because the application of higher pressures leads to dampening of the resonances of the sample.
Samples
RUS can be applied to a great range of samples sizes, with a minimum in the order or a few hundred micrometers, but for the measurement of mineral elasticity it is used on samples typically between 1 mm and 1 cm in size. The sample, either a fully densepolycrystalline
A crystallite is a small or even microscopic crystal which forms, for example, during the cooling of many materials. Crystallites are also referred to as grains.
Bacillite is a type of crystallite. It is rodlike with parallel longulites.
S ...
aggregate or a single crystal
In materials science, a single crystal (or single-crystal solid or monocrystalline solid) is a material in which the crystal lattice of the entire sample is continuous and unbroken to the edges of the sample, with no Grain boundary, grain bound ...
, is machined in to a regular shape. Theoretically any sample shape can be used, but you obtain a substantial saving in computational time using rectangular parallelepiped resonators (RPR), spherical or cylindrical ones (less time savings with cylinders).
 Since the accuracy of the measure depends strictly on the accuracy in the sample preparation, several precautions are taken: RPRs are prepared with the edges parallel to crystallographic directions; for cylinders only the axis can be matched to sample
Since the accuracy of the measure depends strictly on the accuracy in the sample preparation, several precautions are taken: RPRs are prepared with the edges parallel to crystallographic directions; for cylinders only the axis can be matched to sample symmetry
Symmetry () in everyday life refers to a sense of harmonious and beautiful proportion and balance. In mathematics, the term has a more precise definition and is usually used to refer to an object that is Invariant (mathematics), invariant und ...
. RUS is rarely used for samples of lower symmetry, and for isotropic
In physics and geometry, isotropy () is uniformity in all orientations. Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix ' or ', hence '' anisotropy''. ''Anisotropy'' is also ...
samples, alignment is irrelevant. For the higher symmetries, it is convenient to have different lengths edges to prevent a redundant resonance.
Measurements on single crystals require orientation of the sample crystallographic axes with the edges of the RPR, to neglect the orientation computation and deal only with elastic moduli.
Polycrystalline samples should ideally be fully dense, free of cracks and without preferential orientation of the grains. Single crystal samples must be free of internal defects such as twin walls. The surfaces of all samples must be polished flat and opposite faces should be parallel. Once prepared, the density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be u ...
must be measured accurately as it scales the entire set of elastic moduli.
Transducers
RUS ultrasonic transducers are designed to make dry point contact with the sample. This is due to the requirement forfree surface
In physics, a free surface is the surface of a fluid that is subject to zero parallel shear stress,
such as the interface between two homogeneous fluids.
An example of two such homogeneous fluids would be a body of water (liquid) and the air in ...
boundary conditions for the computation of elastic moduli from frequencies. For RPRs this requires a very light touch between the sample's corners and the transducers. Corners are used because they provide elastically weak coupling, reducing loading, and because they are never vibrational node points. Sufficiently weak contact ensures no transduced correction is required.
Applications
As a versatile tool for characterizing elastic properties ofsolid
Solid is a state of matter where molecules are closely packed and can not slide past each other. Solids resist compression, expansion, or external forces that would alter its shape, with the degree to which they are resisted dependent upon the ...
materials, RUS has found applications in a variety of fields.
In geosciences
Earth science or geoscience includes all fields of natural science related to the planet Earth. This is a branch of science dealing with the physical, chemical, and biological complex constitutions and synergistic linkages of Earth's four spheres ...
one of the most important applications is related to the determination of seismic velocities in the Earth's interior. In a recent work, for example, the elastic constants of hydrous forsterite
Forsterite (Mg2SiO4; commonly abbreviated as Fo; also known as white olivine) is the magnesium-rich Endmember, end-member of the olivine solid solution series. It is Isomorphism (crystallography), isomorphous with the iron-rich end-member, fayalit ...
were measured up to 14.1 GPa at ambient temperature. This study showed that aggregate bulk and shear moduli of hydrous forsterite increase with pressure at a greater rate than those of the corresponding anhydrous
A substance is anhydrous if it contains no water. Many processes in chemistry can be impeded by the presence of water; therefore, it is important that water-free reagents and techniques are used. In practice, however, it is very difficult to achie ...
phase. This implies that at ambient conditions VP and VS of hydrous forsterite are slower than those of anhydrous one; conversely, with increasing pressure, and consequently depth, VP and VS of hydrous forsterite exceed those of anhydrous one. In addition hydration decreases the VP/VS ratio of forsterite, the maximum compressional wave
Longitudinal waves are waves which oscillate in the direction which is parallel to the direction in which the wave travels and displacement of the medium is in the same (or opposite) direction of the wave propagation. Mechanical longitudinal w ...
azimuthal anisotropy
Anisotropy () is the structural property of non-uniformity in different directions, as opposed to isotropy. An anisotropic object or pattern has properties that differ according to direction of measurement. For example, many materials exhibit ve ...
and the maximum shear wave
__NOTOC__
In seismology and other areas involving elastic waves, S waves, secondary waves, or shear waves (sometimes called elastic S waves) are a type of elastic wave and are one of the two main types of elastic body waves, so named because t ...
splitting. These data help us to constrain Earth's mantle
Earth's mantle is a layer of silicate mineral, silicate rock between the Earth's crust, crust and the Earth's outer core, outer core. It has a mass of and makes up 67% of the mass of Earth. It has a thickness of making up about 46% of Earth's ...
composition and distinguish regions of hydrogen
Hydrogen is a chemical element; it has chemical symbol, symbol H and atomic number 1. It is the lightest and abundance of the chemical elements, most abundant chemical element in the universe, constituting about 75% of all baryon, normal matter ...
enrichment from regions of high temperature or partial melt.
References
{{reflist Ultrasound