Particle statistics is a particular description of multiple

particle In the physical sciences, a particle (or corpuscule in older texts) is a small localized object which can be described by several physical or chemical properties, such as volume, density, or mass. They vary greatly in size or quantity, fro ...

s in statistical mechanics. A key prerequisite concept is that of a

statistical ensemble In physics, specifically statistical mechanics, an ensemble (also statistical ensemble) is an idealization consisting of a large number of virtual copies (sometimes infinitely many) of a system, considered all at once, each of which represents ...

(an idealization comprising the

state space A state space is the set of all possible configurations of a system. It is a useful abstraction for reasoning about the behavior of a given system and is widely used in the fields of artificial intelligence and game theory. For instance, the t ...

of possible states of a system, each labeled with a probability) that emphasizes properties of a large system as a whole at the expense of knowledge about parameters of separate particles. When an ensemble describes a system of particles with similar properties, their number is called the

particle number The particle number (or number of particles) of a thermodynamic system, conventionally indicated with the letter ''N'', is the number of constituent particles in that system. The particle number is a fundamental parameter in thermodynamics which i ...

and usually denoted by ''N''.

Classical statistics

classical mechanics Classical mechanics is a physical theory describing the motion of macroscopic objects, from projectiles to parts of machinery, and astronomical objects, such as spacecraft, planets, stars, and galaxies. For objects governed by classical ...

, all particles ( fundamental and composite particles, atoms, molecules, electrons, etc.) in the system are considered distinguishable. This means that individual particles in a system can be tracked. As a consequence, switching the positions of any pair of particles in the system leads to a different configuration of the system. Furthermore, there is no restriction on placing more than one particle in any given state accessible to the system. These characteristics of classical positions are called

Maxwell–Boltzmann statistics In statistical mechanics, Maxwell–Boltzmann statistics describes the distribution of classical material particles over various energy states in thermal equilibrium. It is applicable when the temperature is high enough or the particle density ...

Quantum statistics

The fundamental feature of

quantum mechanics Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, q ...

that distinguishes it from classical mechanics is that particles of a particular type are indistinguishable from one another. This means that in an ensemble of similar particles, interchanging any two particles does not lead to a new configuration of the system. In the language of quantum mechanics this means that the

wave function A wave function in quantum physics is a mathematical description of the quantum state of an isolated quantum system. The wave function is a complex-valued probability amplitude, and the probabilities for the possible results of measurements m ...

of the system is invariant up to a phase with respect to the interchange of the constituent particles. In the case of a system consisting of particles of different kinds (for example, electrons and protons), the wave function of the system is invariant up to a phase separately for both assemblies of particles. The applicable definition of a particle does not require it to be

elementary Elementary may refer to: Arts, entertainment, and media Music * ''Elementary'' (Cindy Morgan album), 2001 * ''Elementary'' (The End album), 2007 * ''Elementary'', a Melvin "Wah-Wah Watson" Ragin album, 1977 Other uses in arts, entertainment, a ...

or even "microscopic", but it requires that all its

degrees of freedom Degrees of freedom (often abbreviated df or DOF) refers to the number of independent variables or parameters of a thermodynamic system. In various scientific fields, the word "freedom" is used to describe the limits to which physical movement or ...

(or ''internal states'') that are relevant to the physical problem considered shall be known. All quantum particles, such as

lepton In particle physics, a lepton is an elementary particle of half-integer spin (spin (physics), spin ) that does not undergo strong interactions. Two main classes of leptons exist: electric charge, charged leptons (also known as the electron-li ...

s and

baryon In particle physics, a baryon is a type of composite subatomic particle which contains an odd number of valence quarks (at least 3). Baryons belong to the hadron family of particles; hadrons are composed of quarks. Baryons are also classi ...

s, in the universe have three translational motion degrees of freedom (represented with the wave function) and one discrete degree of freedom, known as spin. Progressively more "complex" particles obtain progressively more internal freedoms (such as various quantum numbers in an

atom Every atom is composed of a nucleus and one or more electrons bound to the nucleus. The nucleus is made of one or more protons and a number of neutrons. Only the most common variety of hydrogen has no neutrons. Every solid, liquid, gas ...

), and, when the number of internal states that "identical" particles in an ensemble can occupy dwarfs their count (the particle number), then effects of quantum statistics become negligible. That's why quantum statistics is useful when one considers, say, helium liquid or

ammonia Ammonia is an inorganic compound of nitrogen and hydrogen with the formula . A stable binary hydride, and the simplest pnictogen hydride, ammonia is a colourless gas with a distinct pungent smell. Biologically, it is a common nitrogeno ...

gas (its

molecule A molecule is a group of two or more atoms held together by attractive forces known as chemical bonds; depending on context, the term may or may not include ions which satisfy this criterion. In quantum physics, organic chemistry, and bio ...

s have a large, but conceivable number of internal states), but is useless applied to systems constructed of

macromolecule A macromolecule is a very large molecule important to biophysical processes, such as a protein or nucleic acid. It is composed of thousands of covalently bonded atoms. Many macromolecules are polymers of smaller molecules called monomers. ...

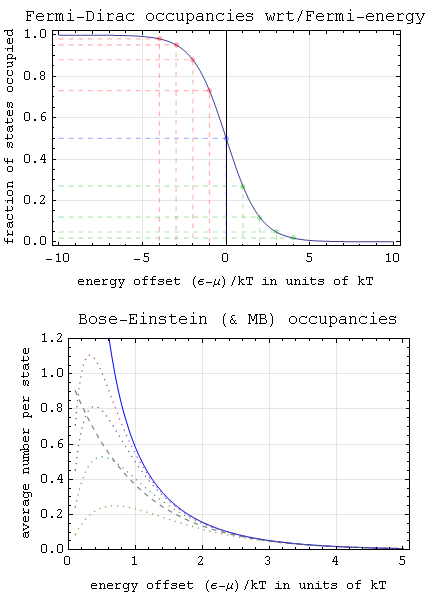
s. While this difference between classical and quantum descriptions of systems is fundamental to all of quantum statistics, quantum particles are divided into two further classes on the basis of the symmetry of the system. The spin–statistics theorem binds two particular kinds of combinatorial symmetry with two particular kinds of spin symmetry, namely bosons and fermions.

Classical statistics

Quantum statistics

See also