Non-random two-liquid model

The non-random two-liquid model (abbreviated NRTL model) is an activity coefficient model introduced by Renon
and Prausnitz in 1968 that correlates the activity coefficients $\gamma_i$ of a compound with its mole fractions $x_i$ in the liquid phase concerned. It is frequently applied in the field of chemical engineering to calculate phase equilibria. The concept of NRTL is based on the hypothesis of Wilson, who stated that the local concentration around a molecule in most mixtures is different from the bulk concentration. This difference is due to a difference between the interaction energy of the central molecule with the molecules of its own kind $U_$ and that with the molecules of the other kind $U_$. The energy difference also introduces a non-randomness at the local molecular level. The NRTL model belongs to the so-called local-composition models. Other models of this type are the Wilson model, the UNIQUAC model, and the group contribution model UNIFAC. These local-composition models are not thermodynamically consistent for a one-fluid model for a real mixture due to the assumption that the local composition around molecule ''i'' is independent of the local composition around molecule ''j''. This assumption is not true, as was shown by Flemr in 1976. However, they are consistent if a hypothetical two-liquid model is used. Models, which have consistency between bulk and the local molecular concentrations around different types of molecules are COSMO-RS, and COSMOSPACE.

Derivation

Like Wilson (1964), Renon & Prausnitz (1968) began with local composition theory, but instead of using the Flory–Huggins volumetric expression as Wilson did, they assumed local compositions followed
:$\frac = \frac \frac$

with a new "non-randomness" parameter α. The excess Gibbs free energy was then determined to be
:$\frac = \sum_i^N x_i \frac$.

Unlike Wilson's equation, this can predict partially miscible mixtures. However, the cross term, like Wohl's expansion, is more suitable for $H^\text$ than $G^\text$, and experimental data is not always sufficiently plentiful to yield three meaningful values, so later attempts to extend Wilson's equation to partial miscibility (or to extend Guggenheim's quasichemical theory for nonrandom mixtures to Wilson's different-sized molecules) eventually yielded variants like UNIQUAC.

Equations for a binary mixture

For a binary mixture the following functions are used:

:
\left\{\begin{matrix} \ln\ \gamma_1=x^2_2\left tau_{21}\left(\frac{G_{21{x_1+x_2 G_{21\right)^2 +\frac{\tau_{12} G_{12 {(x_2+x_1 G_{12})^2 }\right\\
\\ \ln\ \gamma_2=x^2_1\left tau_{12}\left(\frac{G_{12{x_2+x_1 G_{12\right)^2 +\frac{\tau_{21} G_{21 {(x_1+x_2 G_{21})^2 }\right\end{matrix}\right.

with

:$\left\{\begin{matrix} \ln\ G_{12}=-\alpha_{12}\ \tau_{12} \\ \ln\ G_{21}=-\alpha_{21}\ \tau_{21} \end{matrix}\right.$

Here, $\tau_{12}$ and $\tau_{21}$ are the dimensionless interaction parameters, which are related to the interaction energy parameters $\Delta g_{12}$ and $\Delta g_{21}$ by:

:$\left\{\begin{matrix} \tau_{12}=\frac{\Delta g_{12{RT}=\frac{U_{12}-U_{22{RT} \\ \tau_{21}=\frac{\Delta g_{21{RT}=\frac{U_{21}-U_{11{RT} \end{matrix}\right.$

Here ''R'' is the gas constant and ''T'' the absolute temperature, and ''U_ij'' is the energy between molecular surface ''i'' and ''j''. ''U_ii'' is the energy of evaporation. Here ''U_ij'' has to be equal to ''U_ji'', but $\Delta g_{ij}$ is not necessary equal to $\Delta g_{ji}$.

The parameters $\alpha_{12}$ and $\alpha_{21}$ are the so-called non-randomness parameter, for which usually $\alpha_{12}$ is set equal to $\alpha_{21}$. For a liquid, in which the local distribution is random around the center molecule, the parameter $\alpha_{12}=0$. In that case, the equations reduce to the one-parameter Margules activity model:

:
\left\{\begin{matrix} \ln\ \gamma_1=x^2_2\left tau_{21} +\tau_{12} \rightAx^2_2
\\ \ln\ \gamma_2=x^2_1\left tau_{12}+\tau_{21} \rightAx^2_1
\end{matrix}\right.

In practice, $\alpha_{12}$ is set to 0.2, 0.3 or 0.48. The latter value is frequently used for aqueous systems. The high value reflects the ordered structure caused by hydrogen bonds. However, in the description of liquid-liquid equilibria, the non-randomness parameter is set to 0.2 to avoid wrong liquid-liquid description. In some cases, a better phase equilibria description is obtained by setting $\alpha_{12}=-1$. However this mathematical solution is impossible from a physical point of view since no system can be more random than random ($\alpha_{12}=0$). In general, NRTL offers more flexibility in the description of phase equilibria than other activity models due to the extra non-randomness parameters. However, in practice this flexibility is reduced in order to avoid wrong equilibrium description outside the range of regressed data.

The limiting activity coefficients, also known as the activity coefficients at infinite dilution, are calculated by:

:
\left\{\begin{matrix} \ln\ \gamma_1^\infty=\left tau_{21} +\tau_{12} \exp{(-\alpha_{12}\ \tau_{12})} \right\\ \ln\ \gamma_2^\infty=\left tau_{12} +\tau_{21}\exp{(-\alpha_{12}\ \tau_{21})}\right\end{matrix}\right.

The expressions show that at $\alpha_{12}=0$, the limiting activity coefficients are equal. This situation occurs for molecules of equal size but of different polarities.
It also shows, since three parameters are available, that multiple sets of solutions are possible.

General equations

The general equation for $\ln(\gamma_i)$ for species $i$ in a mixture of $n$ components is:

:$\ln(\gamma_i)=\frac{\displaystyle\sum_{j=1}^{n}{x_{j}\tau_{ji}G_{ji}{\displaystyle\sum_{k=1}^{n}{x_{k}G_{ki}+\sum_{j=1}^{n}{\frac{x_{j}G_{ij{\displaystyle\sum_{k=1}^{n}{x_{k}G_{kj {\left ({\tau_{ij}-\frac{\displaystyle\sum_{m=1}^{n}{x_{m}\tau_{mj}G_{mj}{\displaystyle\sum_{k=1}^{n}{x_{k}G_{kj \right )}$

with

:$G_{ij}=\exp\left ({-\alpha_{ij}\tau_{ij\right )$
:$\alpha_{ij}=\alpha_{ij_{0+\alpha_{ij_{1T$
:$\tau_{i,j}=A_{ij}+\frac{B_{ij{T}+\frac{C_{ij{T^{2+D_{ij}\ln{\left ({T}\right )}+E_{ij}T^{F_{ij$

There are several different equation forms for $\alpha_{ij}$ and $\tau_{ij}$, the most general of which are shown above.

Temperature dependent parameters

To describe phase equilibria over a large temperature regime, i.e. larger than 50 K, the interaction parameter has to be made temperature dependent.
Two formats are frequently used. The extended Antoine equation format:

:$\tau_{ij}=f(T)=a_{ij}+\frac{b_{ij{T}+c_{ij}\ \ln\ T+d_{ij}T$

Here the logarithmic and linear terms are mainly used in the description of liquid-liquid equilibria (miscibility gap).

The other format is a second-order polynomial format:
:$\Delta g_{ij}=f(T)=a_{ij}+b_{ij}\cdot T +c_{ij}T^{2}$

Parameter determination

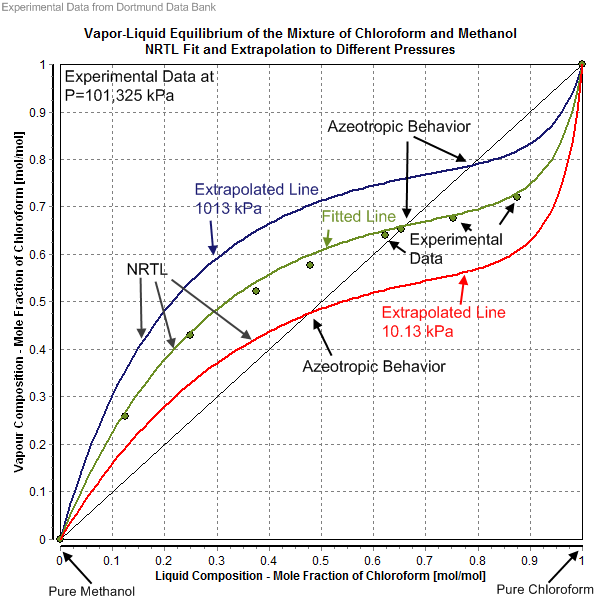
The NRTL parameters are fitted to activity coefficients that have been derived from experimentally determined phase equilibrium data (vapor–liquid, liquid–liquid, solid–liquid) as well as from heats of mixing. The source of the experimental data are often factual data banks like the Dortmund Data Bank. Other options are direct experimental work and predicted activity coefficients with UNIFAC and similar models.
It is noteworthy that for the same mixture several NRTL parameter sets might exist, and the choice of NRTL parameter set depends on the kind of phase equilibrium (i.e. solid–liquid (SL), liquid–liquid (LL), vapor–liquid (VL)). In the case of vapor–liquid equilibria, the fitted result importantly depends on which saturated vapor pressure of the pure components was used, and whether the gas phase was treated as an ideal or a real gas. Accurate saturated vapor pressure values are important in the determination or the description of an azeotrope. The gas fugacity coefficients are mostly set to unity (ideal gas assumption), but for vapor-liquid equilibria at high pressures (i.e. > 10 bar) an equation of state is needed to calculate the gas fugacity coefficient for a real gas description.

Determination of NRTL parameters from regression of LLE and VLE experimental data is a challenging problem because it involves solving isoactivity or isofugacity equations which are highly non-linear. In addition, parameters obtained from LLE of VLE may not always represent the experimental behaviour expected. For this reason it is necessary to confirm the thermodynamic consistency of the obtained parameters in the whole range of compositions (including binary subsystems, experimental and calculated tie-lines, calculated plait point locations from the Hessian matrix, etc.) by using a phase stability test such as the Gibbs free energy minor tangent criteria.

Parameters for NRTL model

NRTL binary interaction parameters have been published in the Dechema data series and are provided by NIST and DDBST. There also exist machine-learning approaches that are able to predict NRTL parameters by using the SMILES notation for molecules as input.

Literature

{{reflist

Physical chemistry
Thermodynamic models

Engineering thermodynamics