|
COSMOSPACE
COSMOSPACE (COSMO Surface-Pair Activity Coefficient Equation) is an activity coefficient model in which the activity coefficient of the components in a liquid chemical mixture can be related through their molar fraction. It was initially developed as an implicit solution to COSMO-RS. While UNIQUAC is a first order approximation, COSMOSPACE gives the exact solution of a lattice model in which pairwise molecule surfaces interact. Therefore, COSMOSPACE outperforms Uniquac in the description of vapor–liquid and liquid–liquid phase equilibria.Thesis of Dennis Bosse, "Diffusion, Viscosity, and Thermodynamics in Liquid Systems" , Technischen Universität Kaiserslautern (2005)" See also * UNIQUAC * :fr:UNIQUAC, UNIQUAC * COSMOSPACE *Chemical equilibrium *Chemical thermodynamics *Fugacity In chemical thermodynamics, the fugacity of a real gas is an effective partial pressure which replaces the mechanical partial pressure in an accurate computation of the chemical equilibri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
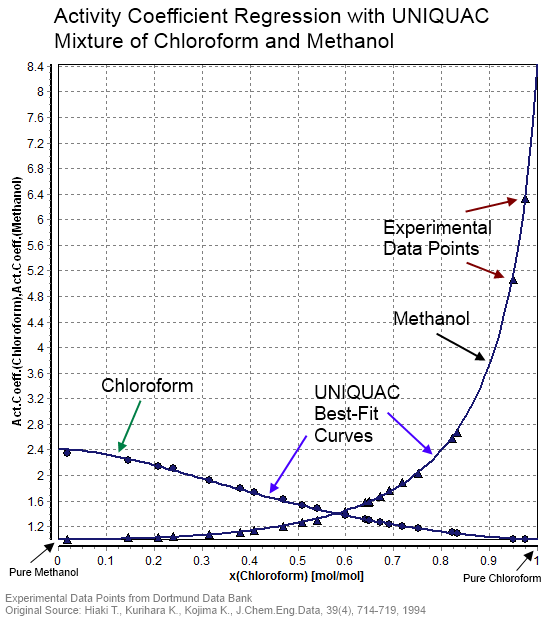
UNIQUAC
In statistical thermodynamics, UNIQUAC (a portmanteau of universal quasichemical) is an activity coefficient model used in description of phase equilibria. The model is a so-called lattice model and has been derived from a first order approximation of interacting molecule surfaces. The model is, however, not fully thermodynamically consistent due to its two- liquid mixture approach. In this approach the local concentration around one central molecule is assumed to be independent from the local composition around another type of molecule. The UNIQUAC model can be considered a second generation activity coefficient because its expression for the excess Gibbs energy consists of an entropy term in addition to an enthalpy term. Earlier activity coefficient models such as the Wilson equation and the non-random two-liquid model (NRTL model) only consist of enthalpy terms. Today the UNIQUAC model is frequently applied in the description of phase equilibria (i.e. liquid–solid, liqui ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Activity Coefficient
In thermodynamics, an activity coefficient is a factor used to account for deviation of a mixture of chemical substances from ideal behaviour. In an ideal mixture, the microscopic interactions between each pair of chemical species are the same (or macroscopically equivalent, the enthalpy change of solution and volume variation in mixing is zero) and, as a result, properties of the mixtures can be expressed directly in terms of simple concentrations or partial pressures of the substances present e.g. Raoult's law. Deviations from ideality are accommodated by modifying the concentration by an ''activity coefficient''. Analogously, expressions involving gases can be adjusted for non-ideality by scaling partial pressures by a fugacity coefficient. The concept of activity coefficient is closely linked to that of activity in chemistry. Thermodynamic definition The chemical potential, \mu_\mathrm, of a substance B in an ideal mixture of liquids or an ideal solution is given by :\mu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Implicit Function
In mathematics, an implicit equation is a relation of the form R(x_1, \dots, x_n) = 0, where is a function of several variables (often a polynomial). For example, the implicit equation of the unit circle is x^2 + y^2 - 1 = 0. An implicit function is a function that is defined by an implicit equation, that relates one of the variables, considered as the value of the function, with the others considered as the arguments. For example, the equation x^2 + y^2 - 1 = 0 of the unit circle defines as an implicit function of if , and is restricted to nonnegative values. The implicit function theorem provides conditions under which some kinds of implicit equations define implicit functions, namely those that are obtained by equating to zero multivariable functions that are continuously differentiable. Examples Inverse functions A common type of implicit function is an inverse function. Not all functions have a unique inverse function. If is a function of that has a unique inv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
COSMO-RS
COSMO-RS (short for COnductor like Screening MOdel for Real Solvents)"Conductor-like Screening Model for Real Solvents: A New Approach to the Quantitative Calculation of Solvation Phenomena", A. Klamt, J. Phys. Chem., 99, 2224-2235 (1995), DOI: 10.1021/j100007a062/ref> is a quantum chemistry based equilibrium thermodynamics method with the purpose of predicting chemical potentials µ in liquids. It processes the screening charge density σ on the surface of molecules to calculate the chemical potential µ of each species in solution. Perhaps in dilute solution a constant potential must be considered. As an initial step a quantum chemical COSMO calculation for all molecules is performed and the results (e.g. the screening charge density) are stored in a database. In a separate step COSMO-RS uses the stored COSMO results to calculate the chemical potential of the molecules in a liquid solvent or mixture. The resulting chemical potentials are the basis for other thermodynamic equilibri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orders Of Approximation
In science, engineering, and other quantitative disciplines, order of approximation refers to formal or informal expressions for how accurate an approximation is. Usage in science and engineering In formal expressions, the ordinal number used before the word order refers to the highest power in the series expansion used in the approximation. The expressions: a ''zeroth-order approximation'', a ''first-order approximation'', a ''second-order approximation'', and so forth are used as fixed phrases. The expression a ''zero-order approximation'' is also common. Cardinal numerals are occasionally used in expressions like an ''order-zero approximation'', an ''order-one approximation'', etc. The omission of the word ''order'' leads to phrases that have less formal meaning. Phrases like first approximation or to a first approximation may refer to ''a roughly approximate value of a quantity''. [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Equilibrium
In thermodynamics, the phase rule is a general principle governing "pVT" systems, whose thermodynamic states are completely described by the variables pressure (), volume () and temperature (), in thermodynamic equilibrium. If is the number of degrees of freedom, is the number of components and is the number of phases, then :F = C - P + 2 It was derived by American physicist Josiah Willard Gibbs in his landmark paper titled ''On the Equilibrium of Heterogeneous Substances'', published in parts between 1875 and 1878. The rule assumes the components do not react with each other. The number of degrees of freedom is the number of independent intensive variables, i.e. the largest number of thermodynamic parameters such as temperature or pressure that can be varied simultaneously and arbitrarily without determining one another. An example of one-component system is a system involving one pure chemical, while two-component systems, such as mixtures of water and ethanol, have two chem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chemical Equilibrium
In a chemical reaction, chemical equilibrium is the state in which both the reactants and products are present in concentrations which have no further tendency to change with time, so that there is no observable change in the properties of the system. This state results when the forward reaction proceeds at the same rate as the reverse reaction. The reaction rates of the forward and backward reactions are generally not zero, but they are equal. Thus, there are no net changes in the concentrations of the reactants and products. Such a state is known as dynamic equilibrium. Historical introduction The concept of chemical equilibrium was developed in 1803, after Berthollet found that some chemical reactions are reversible. For any reaction mixture to exist at equilibrium, the rates of the forward and backward (reverse) reactions must be equal. In the following chemical equation, arrows point both ways to indicate equilibrium. A and B are reactant chemical species, S and T a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chemical Thermodynamics
Chemical thermodynamics is the study of the interrelation of heat and work with chemical reactions or with physical changes of state within the confines of the laws of thermodynamics. Chemical thermodynamics involves not only laboratory measurements of various thermodynamic properties, but also the application of mathematical methods to the study of chemical questions and the ''spontaneity'' of processes. The structure of chemical thermodynamics is based on the first two laws of thermodynamics. Starting from the first and second laws of thermodynamics, four equations called the "fundamental equations of Gibbs" can be derived. From these four, a multitude of equations, relating the thermodynamic properties of the thermodynamic system can be derived using relatively simple mathematics. This outlines the mathematical framework of chemical thermodynamics. History In 1865, the German physicist Rudolf Clausius, in his ''Mechanical Theory of Heat'', suggested that the principles of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fugacity
In chemical thermodynamics, the fugacity of a real gas is an effective partial pressure which replaces the mechanical partial pressure in an accurate computation of the chemical equilibrium constant. It is equal to the pressure of an ideal gas which has the same temperature and molar Gibbs free energy as the real gas. Fugacities are determined experimentally or estimated from various models such as a Van der Waals gas that are closer to reality than an ideal gas. The real gas pressure and fugacity are related through the dimensionless fugacity coefficient . \varphi = \frac For an ideal gas, fugacity and pressure are equal and so . Taken at the same temperature and pressure, the difference between the molar Gibbs free energies of a real gas and the corresponding ideal gas is equal to . The fugacity is closely related to the thermodynamic activity. For a gas, the activity is simply the fugacity divided by a reference pressure to give a dimensionless quantity. This reference ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |