Maxwell–Boltzmann distribution

In physics (in particular in statistical mechanics), the Maxwell–Boltzmann distribution, or Maxwell(ian) distribution, is a particular probability distribution named after James Clerk Maxwell and Ludwig Boltzmann.

It was first defined and used for describing particle speeds in idealized gases, where the particles move freely inside a stationary container without interacting with one another, except for very brief collisions in which they exchange energy and momentum with each other or with their thermal environment. The term "particle" in this context refers to gaseous particles only ( atoms or molecules), and the system of particles is assumed to have reached thermodynamic equilibrium.''Statistical Physics'' (2nd Edition), F. Mandl, Manchester Physics, John Wiley & Sons, 2008, The energies of such particles follow what is known as Maxwell–Boltzmann statistics, and the statistical distribution of speeds is derived by equating particle energies with kinetic energy.

Mathematically, the Maxwell–Boltzmann distribution is the chi distribution with three degrees of freedom (the components of the velocity vector in Euclidean space), with a scale parameter measuring speeds in units proportional to the square root of $T/m$ (the ratio of temperature and particle mass).

The Maxwell–Boltzmann distribution is a result of the kinetic theory of gases, which provides a simplified explanation of many fundamental gaseous properties, including pressure and diffusion. The Maxwell–Boltzmann distribution applies fundamentally to particle velocities in three dimensions, but turns out to depend only on the speed (the magnitude of the velocity) of the particles. A particle speed probability distribution indicates which speeds are more likely: a randomly chosen particle will have a speed selected randomly from the distribution, and is more likely to be within one range of speeds than another. The kinetic theory of gases applies to the classical ideal gas, which is an idealization of real gases. In real gases, there are various effects (e.g., van der Waals interactions, vortical flow, relativistic speed limits, and quantum exchange interactions) that can make their speed distribution different from the Maxwell–Boltzmann form. However, rarefied gases at ordinary temperatures behave very nearly like an ideal gas and the Maxwell speed distribution is an excellent approximation for such gases. This is also true for ideal plasmas, which are ionized gases of sufficiently low density.

The distribution was first derived by Maxwell in 1860 on heuristic grounds.See:
* Maxwell, J.C. (1860 A): ''Illustrations of the dynamical theory of gases. Part I. On the motions and collisions of perfectly elastic spheres. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science'', 4th Series, vol.19, pp.19-32


* Maxwell, J.C. (1860 B): ''Illustrations of the dynamical theory of gases. Part II. On the process of diffusion of two or more kinds of moving particles among one another. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science'', 4th Ser., vol.20, pp.21-37

/ref> Boltzmann later, in the 1870s, carried out significant investigations into the physical origins of this distribution. The distribution can be derived on the ground that it maximizes the entropy of the system. A list of derivations are:

# Maximum entropy probability distribution#Distributions with measured constants, Maximum entropy probability distribution in the phase space, with the constraint of conservation of average energy $\langle H \rangle = E$;
# Canonical ensemble.

Distribution function

For a system containing a large number of identical non-interacting, non-relativistic classical particles in themodynamic equilibrium, the fraction of the particles within an infinitesimal element of the three-dimensional velocity space $d^3v$, centered on a velocity vector of magnitude $v$, is given by
$f(v) ~d^3v = \left(\frac\right)^ \, e^ ~ d^3v,$
where $m$ is the particle mass, $k$ is the Boltzmann constant, and $T$ is thermodynamic temperature.
$f(v)$ is a probability distribution function, properly normalized so that $\int f(v) \, d^3 v$ over all velocities is unity.

One can write the element of velocity space as $d^3v = dv_x \, dv_y \, dv_z$, for velocities in a standard Cartesian coordinate system, or as $d^3v = v^2 \, dv \, d\Omega$ in a standard spherical coordinate system, where $d\Omega$ is an element of solid angle.

The Maxwellian distribution function for particles moving in only one direction, if this direction is $x$, is
$f(v_x) ~dv_x = \left(\frac\right)^ \, e^ ~ dv_x,$
which can be obtained by integrating the three-dimensional form given above over $v_y$ and $v_z$.

Recognizing the symmetry of $f(v)$, one can integrate over solid angle and write a probability distribution of speeds as the function

$f(v) = \left(\frac\right)^\, 4\pi v^2 e^.$

This probability density function gives the probability, per unit speed, of finding the particle with a speed near $v$. This equation is simply the Maxwell–Boltzmann distribution (given in the infobox) with distribution parameter $a = \sqrt$.
The Maxwell–Boltzmann distribution is equivalent to the chi distribution with three degrees of freedom and scale parameter $a = \sqrt$.

The simplest ordinary differential equation satisfied by the distribution is:
$k T v f'(v) + f(v) \left(m v^2 - 2 k T\right) = 0,$
$f(1) = \sqrt e^ \left(\frac\right)^$

or in unitless presentation:
$a^2 x f'(x)+\left(x^2-2 a^2\right) f(x)=0,$
$f(1)=\frac.$

With the Darwin–Fowler method of mean values, the Maxwell–Boltzmann distribution is obtained as an exact result.

Relation to the 2D Maxwell–Boltzmann distribution

For particles confined to move in a plane, the speed distribution is given by

$P(s < , \vec, < s + ds) = \frac\exp\left(-\frac\right) ds$

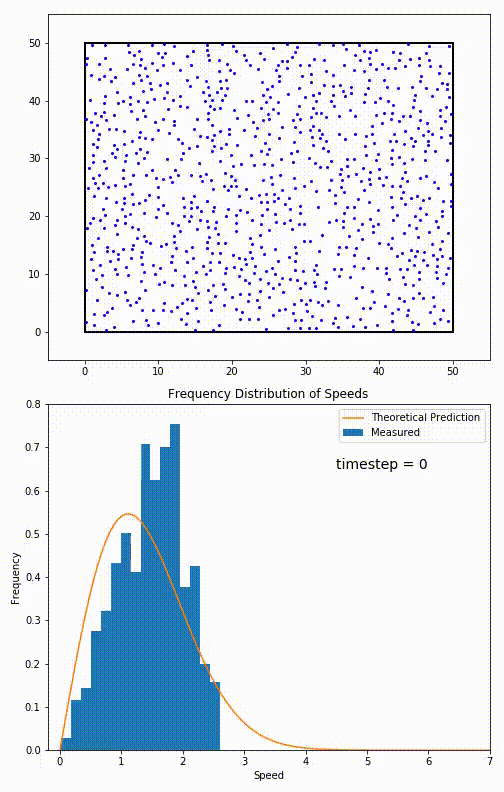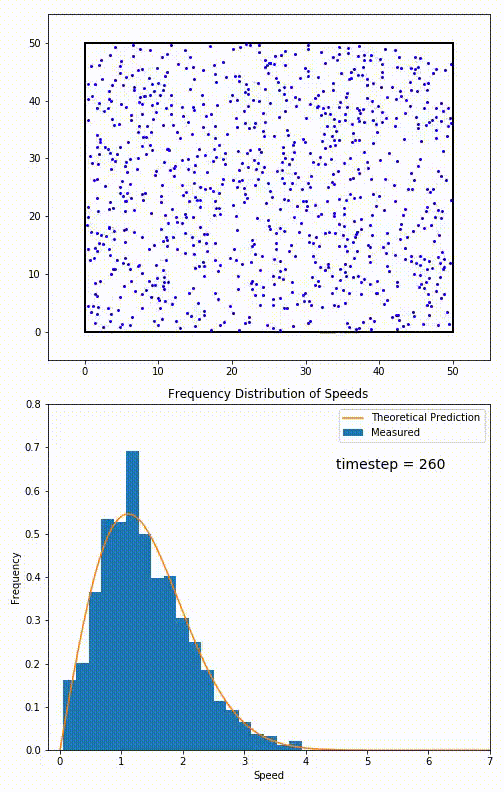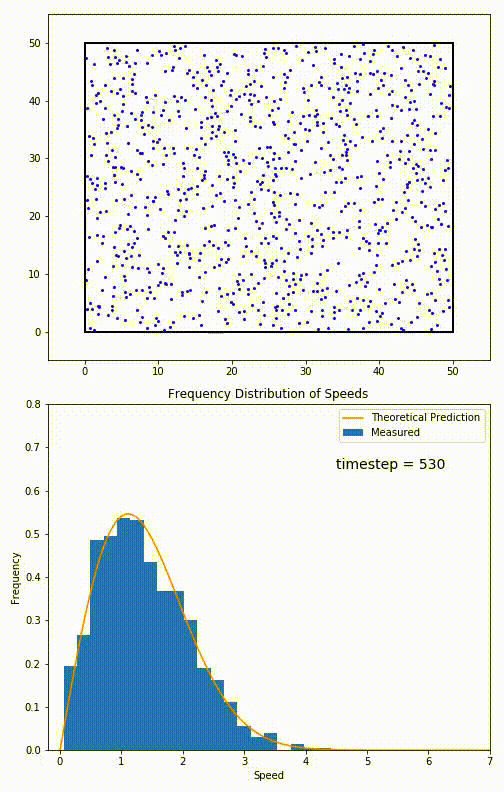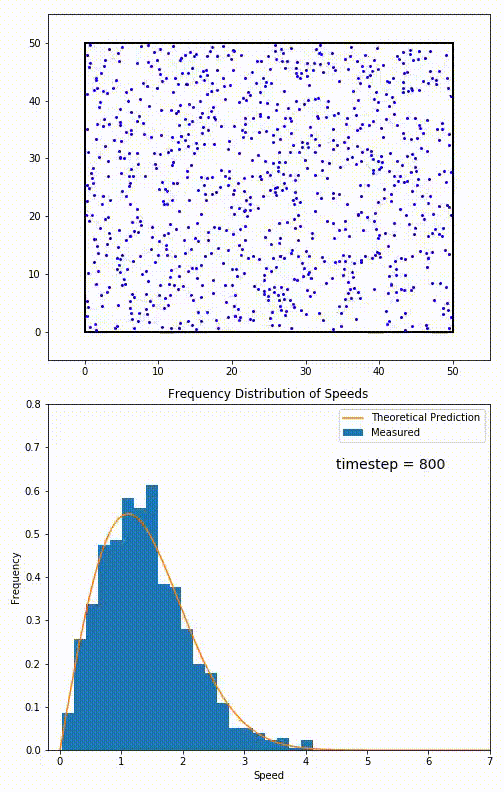
This distribution is used for describing systems in equilibrium. However, most systems do not start out in their equilibrium state. The evolution of a system towards its equilibrium state is governed by the Boltzmann equation. The equation predicts that for short range interactions, the equilibrium velocity distribution will follow a Maxwell–Boltzmann distribution. To the right is a molecular dynamics (MD) simulation in which 900 hard sphere particles are constrained to move in a rectangle. They interact via perfectly elastic collisions. The system is initialized out of equilibrium, but the velocity distribution (in blue) quickly converges to the 2D Maxwell–Boltzmann distribution (in orange).

Typical speeds

The mean speed $\langle v \rangle$, most probable speed ( mode) , and root-mean-square speed $\sqrt$ can be obtained from properties of the Maxwell distribution.

This works well for nearly ideal, monatomic gases like helium, but also for molecular gases like diatomic oxygen. This is because despite the larger heat capacity (larger internal energy at the same temperature) due to their larger number of degrees of freedom, their translational kinetic energy (and thus their speed) is unchanged.

* The most probable speed, , is the speed most likely to be possessed by any molecule (of the same mass ) in the system and corresponds to the maximum value or the mode of . To find it, we calculate the derivative , set it to zero and solve for : $\frac = -8\pi \left(\frac\right)^\ v\ e^ \left(\frac-1\right) = 0$ with the solution: $\frac = 1$ $v_p = \sqrt = \sqrt$ is the gas constant and is molar mass of the substance, and thus may be calculated as a product of particle mass, , and Avogadro constant, : $M = m N_A$For diatomic nitrogen (N₂, the primary component of air) at room temperature (), this gives $v_p \approx \sqrt \approx 422\ \text.$
* The mean speed is the expected value of the speed distribution, setting $b= \frac = \frac$: $\begin \langle v \rangle &= \int_0^ v \, f(v) \, dv \\ &= 4 \pi \left (\frac \right )^\frac \int_^ v^3 e^ dv \\ &= 4 \pi \left (\frac \right )^\frac \frac = \sqrt \\ &= \sqrt = \sqrt = \frac v_p \end$
* The mean square speed $\langle v^2 \rangle$ is the second-order raw moment of the speed distribution. The "root mean square speed" $v_\mathrm$ is the square root of the mean square speed, corresponding to the speed of a particle with median kinetic energy, setting $b = \frac = \frac$:\begin
v_\mathrm
& = \sqrt
= \left(\int_0^ v^2 \, f(v) \, dv \right)^ \\
& = \left( 4 \pi \left (\frac \right )^ \int_^ v^4 e^ dv\right)^ \\
& = \left(4 \pi \left (\frac\right )^ \frac \sqrt \right)^
= \left( \frac \right)^ \\ pt&= \sqrt
= \sqrt
= \sqrt v_p
\end

In summary, the typical speeds are related as follows:
$v_p \approx 88.6\%\ \langle v \rangle < \langle v \rangle < 108.5\%\ \langle v \rangle \approx v_\mathrm.$

The root mean square speed is directly related to the speed of sound in the gas, by
$c = \sqrt\ v_\mathrm = \sqrt\ v_\mathrm = \sqrt\ v_p ,$
where $\gamma = 1 + \frac$ is the adiabatic index, is the number of degrees of freedom of the individual gas molecule. For the example above, diatomic nitrogen (approximating air) at , $f = 5$ and
$c = \sqrtv_\mathrm \approx 68\%\ v_\mathrm \approx 84\%\ v_p \approx 353\ \mathrm,$
the true value for air can be approximated by using the average molar weight of air (), yielding at (corrections for variable humidity are of the order of 0.1% to 0.6%).

The average relative velocity
$v_ \equiv \langle , \vec_1-\vec_2, \rangle = \int \! d^3v_1 \, d^3v_2 \left, \vec_1-\vec_2\ f(\vec_1) f(\vec_2) = \frac\sqrt = \sqrt\langle v \rangle$
where the three-dimensional velocity distribution is
$f(\vec) \equiv \frace^.$

The integral can easily be done by changing to coordinates $\vec = \vec_1-\vec_2$ and $\vec = \frac.$

Derivation and related distributions

Maxwell–Boltzmann statistics

The original derivation in 1860 by James Clerk Maxwell was an argument based on molecular collisions of the Kinetic theory of gases as well as certain symmetries in the speed distribution function; Maxwell also gave an early argument that these molecular collisions entail a tendency towards equilibrium. After Maxwell, Ludwig Boltzmann in 1872 also derived the distribution on mechanical grounds and argued that gases should over time tend toward this distribution, due to collisions (see H-theorem). He later (1877) derived the distribution again under the framework of statistical thermodynamics. The derivations in this section are along the lines of Boltzmann's 1877 derivation, starting with result known as Maxwell–Boltzmann statistics (from statistical thermodynamics). Maxwell–Boltzmann statistics gives the average number of particles found in a given single-particle microstate. Under certain assumptions, the logarithm of the fraction of particles in a given microstate is proportional to the ratio of the energy of that state to the temperature of the system:
$-\log \left(\frac\right) \propto \frac.$
The assumptions of this equation are that the particles do not interact, and that they are classical; this means that each particle's state can be considered independently from the other particles' states. Additionally, the particles are assumed to be in thermal equilibrium.

This relation can be written as an equation by introducing a normalizing factor:

where:
* is the expected number of particles in the single-particle microstate ,
* is the total number of particles in the system,
* is the energy of microstate ,
* the sum over index takes into account all microstates,
* is the equilibrium temperature of the system,
* is the Boltzmann constant.
The denominator in Equation () is a normalizing factor so that the ratios $N_i:N$ add up to unity — in other words it is a kind of partition function (for the single-particle system, not the usual partition function of the entire system).

Because velocity and speed are related to energy, Equation () can be used to derive relationships between temperature and the speeds of gas particles. All that is needed is to discover the density of microstates in energy, which is determined by dividing up momentum space into equal sized regions.

Distribution for the momentum vector

The potential energy is taken to be zero, so that all energy is in the form of kinetic energy.
The relationship between kinetic energy and momentum for massive non- relativistic particles is

where ''p''² is the square of the momentum vector . We may therefore rewrite Equation () as:

where ''Z'' is the partition function, corresponding to the denominator in Equation (). Here ''m'' is the molecular mass of the gas, ''T'' is the thermodynamic temperature and ''k'' is the Boltzmann constant. This distribution of $N_i:N$ is proportional to the probability density function ''f''_p for finding a molecule with these values of momentum components, so:

The normalizing constant can be determined by recognizing that the probability of a molecule having ''some'' momentum must be 1.
Integrating the exponential in () over all ''p''_''x'', ''p''_''y'', and ''p''_''z'' yields a factor of
\iiint_^ \exp \left -\frac\rightdp_x\, dp_y\, dp_z
= \left(\sqrt \sqrt\right)^3

So that the normalized distribution function is:

The distribution is seen to be the product of three independent normally distributed variables $p_x$, $p_y$, and $p_z$, with variance $mkT$. Additionally, it can be seen that the magnitude of momentum will be distributed as a Maxwell–Boltzmann distribution, with $a=\sqrt$. The Maxwell–Boltzmann distribution for the momentum (or equally for the velocities) can be obtained more fundamentally using the H-theorem at equilibrium within the Kinetic theory of gases framework.

Distribution for the energy

The energy distribution is found imposing

where $d^3 \textbf p$ is the infinitesimal phase-space volume of momenta corresponding to the energy interval $dE$.
Making use of the spherical symmetry of the energy-momentum dispersion relation $E = , \textbf p, ^2/2m$, this can be expressed in terms of $dE$ as

Using then () in (), and expressing everything in terms of the energy $E$, we get
$f_E(E) dE = \frac e^ 4 \pi m \sqrt dE = 2 \sqrt \left( \frac \right)^ \exp\left(-\frac \right) dE$
and finally

Since the energy is proportional to the sum of the squares of the three normally distributed momentum components, this energy distribution can be written equivalently as a gamma distribution, using a shape parameter, $k_\text = 3/2$ and a scale parameter, $\theta_\text = kT$.

Using the equipartition theorem, given that the energy is evenly distributed among all three degrees of freedom in equilibrium, we can also split $f_E(E) dE$ into a set of chi-squared distributions, where the energy per degree of freedom, $\epsilon$, is distributed as a chi-squared distribution with one degree of freedom,
Appendix N, page 434

$f_\epsilon\left(\epsilon\right)\,d\epsilon= \sqrt~\exp\left(-\frac\right)\,d\epsilon$

At equilibrium, this distribution will hold true for any number of degrees of freedom. For example, if the particles are rigid mass dipoles of fixed dipole moment, they will have three translational degrees of freedom and two additional rotational degrees of freedom. The energy in each degree of freedom will be described according to the above chi-squared distribution with one degree of freedom, and the total energy will be distributed according to a chi-squared distribution with five degrees of freedom. This has implications in the theory of the specific heat of a gas.

Distribution for the velocity vector

Recognizing that the velocity probability density ''f''_v is proportional to the momentum probability density function by

$f_\mathbf d^3v = f_\mathbf \left(\frac\right)^3 d^3v$

and using p = ''m''v we get

which is the Maxwell–Boltzmann velocity distribution. The probability of finding a particle with velocity in the infinitesimal element about velocity is

$f_\mathbf \left(v_x, v_y, v_z\right)\, dv_x\, dv_y\, dv_z.$

Like the momentum, this distribution is seen to be the product of three independent normally distributed variables $v_x$, $v_y$, and $v_z$, but with variance $\frac$.
It can also be seen that the Maxwell–Boltzmann velocity distribution for the vector velocity
is the product of the distributions for each of the three directions:
$f_\mathbf \left(v_x, v_y, v_z\right) = f_v (v_x)f_v (v_y)f_v (v_z)$
where the distribution for a single direction is
$f_v (v_i) = \sqrt \exp \left(-\frac\right).$

Each component of the velocity vector has a normal distribution with mean $\mu_ = \mu_ = \mu_ = 0$ and standard deviation $\sigma_ = \sigma_ = \sigma_ = \sqrt$, so the vector has a 3-dimensional normal distribution, a particular kind of multivariate normal distribution, with mean $\mu_ = \mathbf$ and covariance $\Sigma_ = \left(\frac\right)I$, where $I$ is the $3\times3$ identity matrix.

Distribution for the speed

The Maxwell–Boltzmann distribution for the speed follows immediately from the distribution of the velocity vector, above. Note that the speed is
$v = \sqrt$
and the volume element in spherical coordinates
$dv_x\, dv_y\, dv_z = v^2 \sin \theta\, dv\, d\theta\, d\phi = v^2 dv \, d\Omega$
where $\phi$ and $\theta$ are the spherical coordinate angles of the velocity vector. Integration of the probability density function of the velocity over the solid angles $d\Omega$ yields an additional factor of $4\pi$.
The speed distribution with substitution of the speed for the sum of the squares of the vector components:

In ''n''-dimensional space

In ''n''-dimensional space, Maxwell–Boltzmann distribution becomes:
$f(v) ~d^nv = \left(\frac\right)^\, e^ ~d^nv$

Speed distribution becomes:
$f(v) ~dv = \text \times e^ \times v^ ~dv$

The following integral result is useful:
\begin
\int_^ v^a e^ dv
&= \left frac\right \int_^ e^x^dx^\\
&= \left frac\right \int_^ e^x^\fracdx\\
&= \left frac\right \frac
\end
where $\Gamma(z)$ is the Gamma function. This result can be used to calculate the moments of speed distribution function:
\begin
\langle v \rangle
&= \frac

\\ pt&= \left frac\right \frac
\end
which is the mean speed itself v_ = \langle v \rangle = \left frac\right \frac.

\begin
\langle v^2 \rangle
&= \frac

\\
&= \left frac\right\frac \\
&= \left frac\right\frac = \frac
\end
which gives root-mean-square speed v_ = \sqrt = \left frac\right .

The derivative of speed distribution function:
$\frac = \text \times \ e^ \left(-\frac v^+(n-1)v^\right) = 0$

This yields the most probable speed ( mode) v_ = \left frac\right.

See also

* Quantum Boltzmann equation
* Maxwell–Boltzmann statistics
* Maxwell–Jüttner distribution
* Boltzmann distribution
* Rayleigh distribution
* Kinetic theory of gases

References

Further reading

* Physics for Scientists and Engineers – with Modern Physics (6th Edition), P. A. Tipler, G. Mosca, Freeman, 2008,
* Thermodynamics, From Concepts to Applications (2nd Edition), A. Shavit, C. Gutfinger, CRC Press (Taylor and Francis Group, USA), 2009,
* Chemical Thermodynamics, D.J.G. Ives, University Chemistry, Macdonald Technical and Scientific, 1971,
* Elements of Statistical Thermodynamics (2nd Edition), L.K. Nash, Principles of Chemistry, Addison-Wesley, 1974,
* Ward, CA & Fang, G 1999, 'Expression for predicting liquid evaporation flux: Statistical rate theory approach', Physical Review E, vol. 59, no. 1, pp. 429–40.
* Rahimi, P & Ward, CA 2005, 'Kinetics of Evaporation: Statistical Rate Theory Approach', International Journal of Thermodynamics, vol. 8, no. 9, pp. 1–14.

External links

"The Maxwell Speed Distribution"
from The Wolfram Demonstrations Project at Mathworld

{{DEFAULTSORT:Maxwell-Boltzmann Distribution
Continuous distributions
Gases
Ludwig Boltzmann
James Clerk Maxwell
Normal distribution
Particle distributions