Logarithmic spiral on:
[Wikipedia]
[Google]
[Amazon]
 A logarithmic spiral, equiangular spiral, or growth spiral is a self-similar spiral
A logarithmic spiral, equiangular spiral, or growth spiral is a self-similar spiral

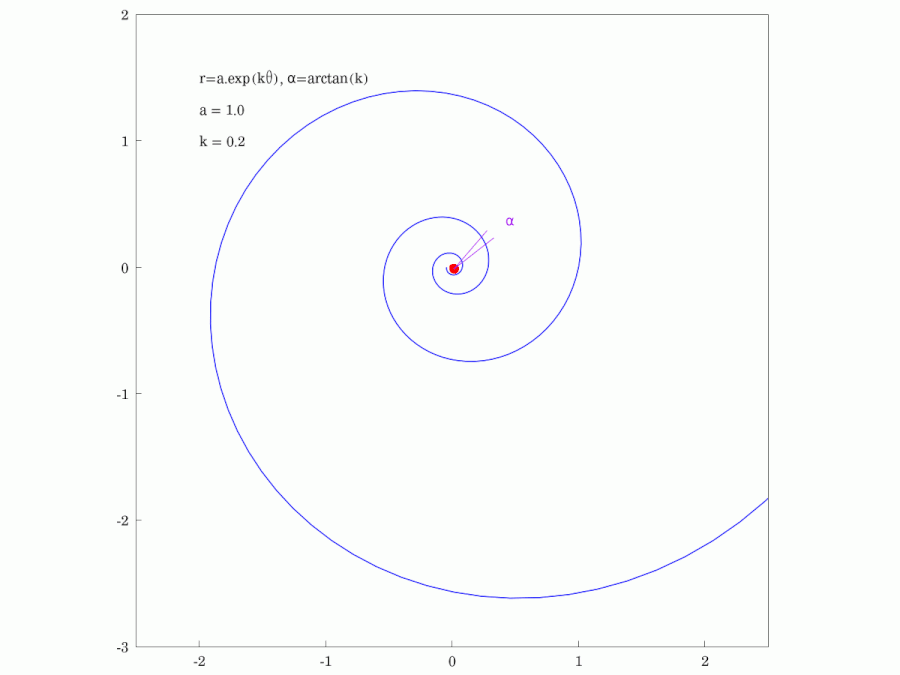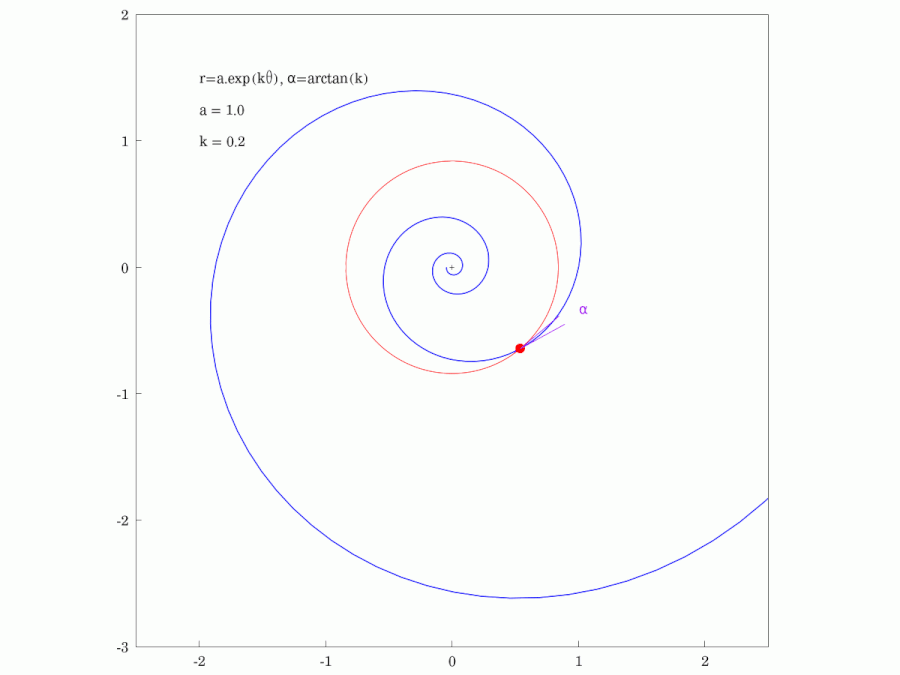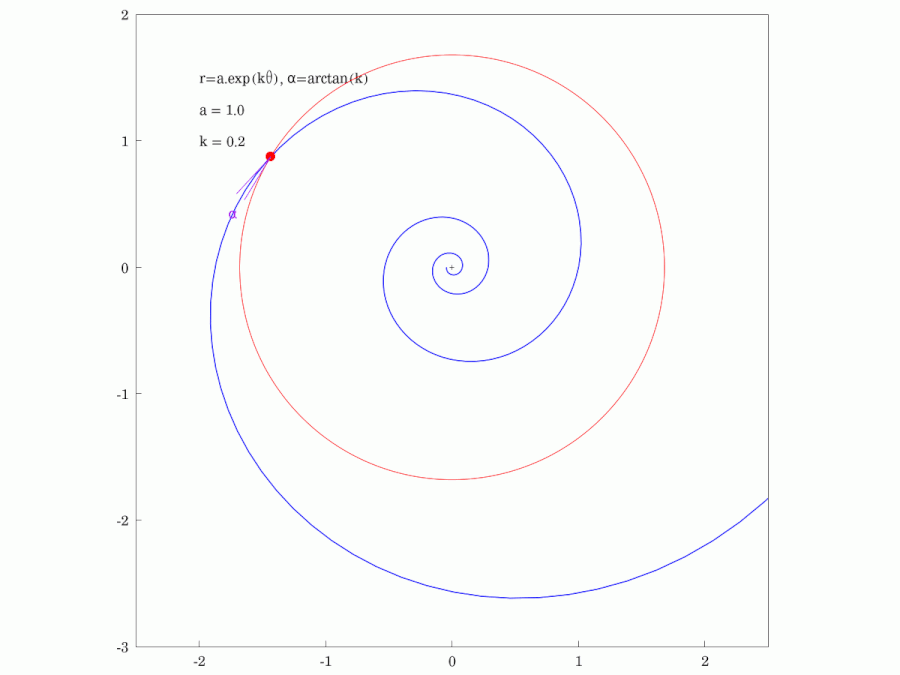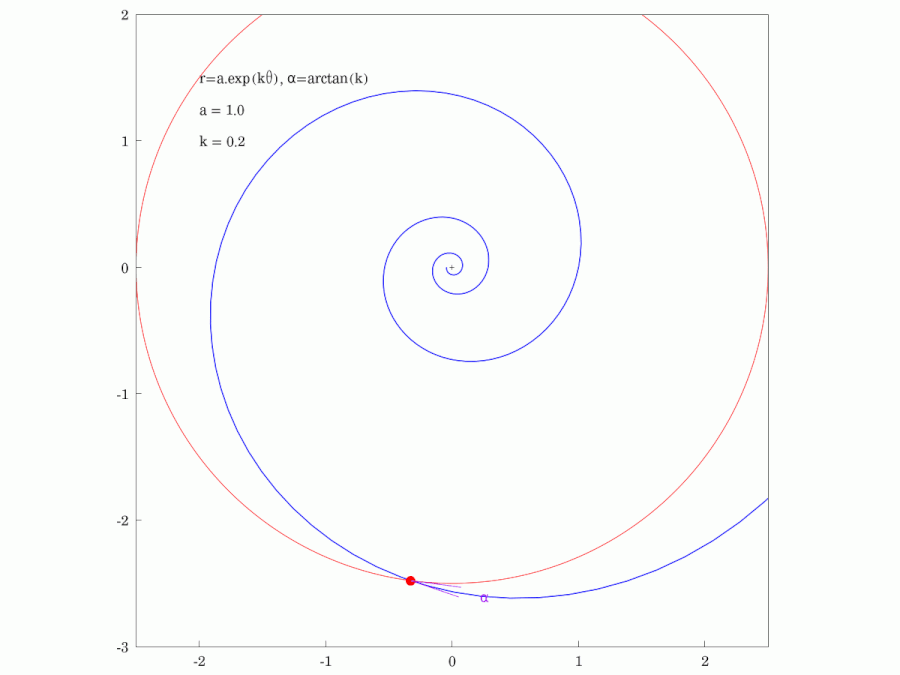 The logarithmic spiral has the following properties (see Spiral):
* Pitch angle: with pitch angle (see diagram and animation).(In case of angle would be 0 and the curve a circle with radius .)
* Curvature:
* Arc length: Especially: , if . This property was first realized by
The logarithmic spiral has the following properties (see Spiral):
* Pitch angle: with pitch angle (see diagram and animation).(In case of angle would be 0 and the curve a circle with radius .)
* Curvature:
* Arc length: Especially: , if . This property was first realized by  * Rotating, scaling: Rotating the spiral by angle yields the spiral , which is the original spiral uniformly scaled (at the origin) by . Scaling by gives the ''same'' curve.
* Self-similarity: A result of the previous property: A scaled logarithmic spiral is congruent (by rotation) to the original curve. ''Example:'' The diagram shows spirals with slope angle and . Hence they are all scaled copies of the red one. But they can also be generated by rotating the red one by angles resp.. All spirals have no points in common (see property on ''complex exponential function'').
* Relation to other curves: Logarithmic spirals are congruent to their own
* Rotating, scaling: Rotating the spiral by angle yields the spiral , which is the original spiral uniformly scaled (at the origin) by . Scaling by gives the ''same'' curve.
* Self-similarity: A result of the previous property: A scaled logarithmic spiral is congruent (by rotation) to the original curve. ''Example:'' The diagram shows spirals with slope angle and . Hence they are all scaled copies of the red one. But they can also be generated by rotating the red one by angles resp.. All spirals have no points in common (see property on ''complex exponential function'').
* Relation to other curves: Logarithmic spirals are congruent to their own
 In several natural phenomena one may find curves that are close to being logarithmic spirals. Here follow some examples and reasons:
*The approach of a hawk to its prey in classical pursuit, assuming the prey travels in a straight line. Their sharpest view is at an angle to their direction of flight; this angle is the same as the spiral's pitch.
*The approach of an insect to a light source. They are used to having the light source at a constant angle to their flight path. Usually the Sun (or Moon for nocturnal species) is the only light source and flying that way will result in a practically straight line. In the same token, a rhumb line approximates a logarithmic spiral close to a pole.
*The arms of spiral galaxies. The
In several natural phenomena one may find curves that are close to being logarithmic spirals. Here follow some examples and reasons:
*The approach of a hawk to its prey in classical pursuit, assuming the prey travels in a straight line. Their sharpest view is at an angle to their direction of flight; this angle is the same as the spiral's pitch.
*The approach of an insect to a light source. They are used to having the light source at a constant angle to their flight path. Usually the Sun (or Moon for nocturnal species) is the only light source and flying that way will result in a practically straight line. In the same token, a rhumb line approximates a logarithmic spiral close to a pole.
*The arms of spiral galaxies. The
Equiangular Spiral (or Logarithmic Spiral) and Its Related Curves
University of Georgia (1999) * Alexander Bogomolny
Spira Mirabilis - Wonderful Spiral
at cut-the-knot
history and math * *
''SpiralZoom.com''
an educational website about the science of pattern formation, spirals in nature, and spirals in the mythic imagination.
Online exploration using JSXGraph (JavaScript)
YouTube lecture on Zeno's mice problem and logarithmic spirals
{{Spirals Spirals Spiral Spiral Plane curves
 A logarithmic spiral, equiangular spiral, or growth spiral is a self-similar spiral
A logarithmic spiral, equiangular spiral, or growth spiral is a self-similar spiral curve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight.
Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that ...
that often appears in nature. The first to describe a logarithmic spiral was Albrecht Dürer
Albrecht Dürer ( , ;; 21 May 1471 – 6 April 1528),Müller, Peter O. (1993) ''Substantiv-Derivation in Den Schriften Albrecht Dürers'', Walter de Gruyter. . sometimes spelled in English as Durer or Duerer, was a German painter, Old master prin ...
(1525) who called it an "eternal line" ("ewige Linie"). More than a century later, the curve was discussed by Descartes (1638), and later extensively investigated by Jacob Bernoulli
Jacob Bernoulli (also known as James in English or Jacques in French; – 16 August 1705) was a Swiss mathematician. He sided with Gottfried Wilhelm Leibniz during the Leibniz–Newton calculus controversy and was an early proponent of Leibniz ...
, who called it ''Spira mirabilis'', "the marvelous spiral".
The logarithmic spiral is distinct from the Archimedean spiral
The Archimedean spiral (also known as Archimedes' spiral, the arithmetic spiral) is a spiral named after the 3rd-century BC Ancient Greece, Greek mathematician Archimedes. The term ''Archimedean spiral'' is sometimes used to refer to the more gene ...
in that the distances between the turnings of a logarithmic spiral increase in a geometric progression, whereas for an Archimedean spiral these distances are constant.
Definition
Inpolar coordinates
In mathematics, the polar coordinate system specifies a given point (mathematics), point in a plane (mathematics), plane by using a distance and an angle as its two coordinate system, coordinates. These are
*the point's distance from a reference ...
the logarithm
In mathematics, the logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of to base is , because is to the rd power: . More generally, if , the ...
ic spiral can be written as
or
with being the base of natural logarithm
The natural logarithm of a number is its logarithm to the base of a logarithm, base of the e (mathematical constant), mathematical constant , which is an Irrational number, irrational and Transcendental number, transcendental number approxima ...
s, and , being real constants.
In Cartesian coordinates
The logarithmic spiral with the polar equation can be represented in Cartesian coordinates by In thecomplex plane
In mathematics, the complex plane is the plane (geometry), plane formed by the complex numbers, with a Cartesian coordinate system such that the horizontal -axis, called the real axis, is formed by the real numbers, and the vertical -axis, call ...
:
''Spira mirabilis'' and Jacob Bernoulli
''Spira mirabilis'',Latin
Latin ( or ) is a classical language belonging to the Italic languages, Italic branch of the Indo-European languages. Latin was originally spoken by the Latins (Italic tribe), Latins in Latium (now known as Lazio), the lower Tiber area aroun ...
for "miraculous spiral", is another name for the logarithmic spiral. Although this curve had already been named by other mathematicians, the specific name ("miraculous" or "marvelous" spiral) was given to this curve by Jacob Bernoulli
Jacob Bernoulli (also known as James in English or Jacques in French; – 16 August 1705) was a Swiss mathematician. He sided with Gottfried Wilhelm Leibniz during the Leibniz–Newton calculus controversy and was an early proponent of Leibniz ...
, because he was fascinated by one of its unique mathematical properties: the size of the spiral increases but its shape is unaltered with each successive curve, a property known as self-similarity. Possibly as a result of this unique property, the spira mirabilis has evolved in nature, appearing in certain growing forms such as nautilus
A nautilus (; ) is any of the various species within the cephalopod family Nautilidae. This is the sole extant family of the superfamily Nautilaceae and the suborder Nautilina.
It comprises nine living species in two genera, the type genus, ty ...
shells and sunflower
The common sunflower (''Helianthus annuus'') is a species of large annual forb of the daisy family Asteraceae. The common sunflower is harvested for its edible oily seeds, which are often eaten as a snack food. They are also used in the pr ...
heads. Jacob Bernoulli wanted such a spiral engraved on his headstone
A gravestone or tombstone is a marker, usually stone, that is placed over a grave. A marker set at the head of the grave may be called a headstone. An especially old or elaborate stone slab may be called a funeral stele, stela, or slab. The u ...
along with the phrase " Eadem mutata resurgo" ("Although changed, I shall arise the same."), but, by error, an Archimedean spiral
The Archimedean spiral (also known as Archimedes' spiral, the arithmetic spiral) is a spiral named after the 3rd-century BC Ancient Greece, Greek mathematician Archimedes. The term ''Archimedean spiral'' is sometimes used to refer to the more gene ...
was placed there instead.
Properties
 The logarithmic spiral has the following properties (see Spiral):
* Pitch angle: with pitch angle (see diagram and animation).(In case of angle would be 0 and the curve a circle with radius .)
* Curvature:
* Arc length: Especially: , if . This property was first realized by
The logarithmic spiral has the following properties (see Spiral):
* Pitch angle: with pitch angle (see diagram and animation).(In case of angle would be 0 and the curve a circle with radius .)
* Curvature:
* Arc length: Especially: , if . This property was first realized by Evangelista Torricelli
Evangelista Torricelli ( ; ; 15 October 160825 October 1647) was an Italian people, Italian physicist and mathematician, and a student of Benedetto Castelli. He is best known for his invention of the barometer, but is also known for his advances i ...
even before calculus
Calculus is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations.
Originally called infinitesimal calculus or "the ...
had been invented.
* Sector area:
* Inversion: Circle inversion
In geometry, inversive geometry is the study of ''inversion'', a transformation of the Euclidean plane that maps circles or lines to other circles or lines and that preserves the angles between crossing curves. Many difficult problems in geometry ...
() maps the logarithmic spiral onto the logarithmic spiral
involute
In mathematics, an involute (also known as an evolvent) is a particular type of curve that is dependent on another shape or curve. An involute of a curve is the Locus (mathematics), locus of a point on a piece of taut string as the string is eith ...
s, evolutes, and the pedal curves based on their centers.
* Complex exponential function: The exponential function exactly maps all lines not parallel with the real or imaginary axis in the complex plane, to all logarithmic spirals in the complex plane with centre at : The pitch angle of the logarithmic spiral is the angle between the line and the imaginary axis.
Special cases and approximations
Thegolden spiral
In geometry, a golden spiral is a logarithmic spiral whose growth factor is , the golden ratio. That is, a golden spiral gets wider (or further from its origin) by a factor of for every quarter Turn (angle), turn it makes.
Approximations of th ...
is a logarithmic spiral that grows outward by a factor of the golden ratio
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their summation, sum to the larger of the two quantities. Expressed algebraically, for quantities and with , is in a golden ratio to if
\fr ...
for every 90 degrees of rotation (pitch angle about 17.03239 degrees). It can be approximated by a "Fibonacci spiral", made of a sequence of quarter circles with radii proportional to Fibonacci number
In mathematics, the Fibonacci sequence is a Integer sequence, sequence in which each element is the sum of the two elements that precede it. Numbers that are part of the Fibonacci sequence are known as Fibonacci numbers, commonly denoted . Many w ...
s.
In nature
 In several natural phenomena one may find curves that are close to being logarithmic spirals. Here follow some examples and reasons:
*The approach of a hawk to its prey in classical pursuit, assuming the prey travels in a straight line. Their sharpest view is at an angle to their direction of flight; this angle is the same as the spiral's pitch.
*The approach of an insect to a light source. They are used to having the light source at a constant angle to their flight path. Usually the Sun (or Moon for nocturnal species) is the only light source and flying that way will result in a practically straight line. In the same token, a rhumb line approximates a logarithmic spiral close to a pole.
*The arms of spiral galaxies. The
In several natural phenomena one may find curves that are close to being logarithmic spirals. Here follow some examples and reasons:
*The approach of a hawk to its prey in classical pursuit, assuming the prey travels in a straight line. Their sharpest view is at an angle to their direction of flight; this angle is the same as the spiral's pitch.
*The approach of an insect to a light source. They are used to having the light source at a constant angle to their flight path. Usually the Sun (or Moon for nocturnal species) is the only light source and flying that way will result in a practically straight line. In the same token, a rhumb line approximates a logarithmic spiral close to a pole.
*The arms of spiral galaxies. The Milky Way
The Milky Way or Milky Way Galaxy is the galaxy that includes the Solar System, with the name describing the #Appearance, galaxy's appearance from Earth: a hazy band of light seen in the night sky formed from stars in other arms of the galax ...
galaxy has several spiral arms, each of which is roughly a logarithmic spiral with pitch of about 12 degrees. However, although spiral galaxies have often been modeled as logarithmic spirals, Archimedean spiral
The Archimedean spiral (also known as Archimedes' spiral, the arithmetic spiral) is a spiral named after the 3rd-century BC Ancient Greece, Greek mathematician Archimedes. The term ''Archimedean spiral'' is sometimes used to refer to the more gene ...
s, or hyperbolic spirals, their pitch angles vary with distance from the galactic center, unlike logarithmic spirals (for which this angle does not vary), and also at variance with the other mathematical spirals used to model them.
*The nerves of the cornea
The cornea is the transparency (optics), transparent front part of the eyeball which covers the Iris (anatomy), iris, pupil, and Anterior chamber of eyeball, anterior chamber. Along with the anterior chamber and Lens (anatomy), lens, the cornea ...
(this is, corneal nerves of the subepithelial layer terminate near superficial epithelial layer of the cornea in a logarithmic spiral pattern).C. Q. Yu CQ and M. I. Rosenblatt, "Transgenic corneal neurofluorescence in mice: a new model for in vivo investigation of nerve structure and regeneration,"
Invest Ophthalmol Vis Sci. 2007 Apr;48(4):1535-42.
*The bands of tropical cyclone
A tropical cyclone is a rapidly rotating storm system with a low-pressure area, a closed low-level atmospheric circulation, strong winds, and a spiral arrangement of thunderstorms that produce heavy rain and squalls. Depending on its locat ...
s, such as hurricanes.
*Many biological structures including the shells of mollusk
Mollusca is a phylum of protostomic invertebrate animals, whose members are known as molluscs or mollusks (). Around 76,000 extant species of molluscs are recognized, making it the second-largest animal phylum after Arthropoda. The ...
s. In these cases, the reason may be construction from expanding similar shapes, as is the case for polygon
In geometry, a polygon () is a plane figure made up of line segments connected to form a closed polygonal chain.
The segments of a closed polygonal chain are called its '' edges'' or ''sides''. The points where two edges meet are the polygon ...
al figures.
* Logarithmic spiral beaches can form as the result of wave refraction and diffraction by the coast. Half Moon Bay (California) is an example of such a type of beach.
In engineering applications
* Logarithmic spiral antennas are frequency-independent antennas, that is, antennas whose radiation pattern, impedance and polarization remain largely unmodified over a wide bandwidth. * When manufacturing mechanisms by subtractive fabrication machines (such as laser cutters), there can be a loss of precision when the mechanism is fabricated on a different machine due to the difference of material removed (that is, the kerf) by each machine in the cutting process. To adjust for this variation of kerf, the self-similar property of the logarithmic spiral has been used to design a kerf cancelling mechanism for laser cutters. *Logarithmic spiral bevel gears are a type of spiral bevel gear whose gear tooth centerline is a logarithmic spiral. A logarithmic spiral has the advantage of providing equal angles between the tooth centerline and the radial lines, which gives the meshing transmission more stability. *Inrock climbing
Rock climbing is a climbing sports discipline that involves ascending climbing routes, routes consisting of natural rock in an outdoor environment, or on artificial resin climbing walls in a mostly indoor environment. Routes are documented in c ...
, spring-loaded camming devices are made from metal cams whose outer gripping surfaces are shaped as arcs of logarithmic spirals. When the device is inserted into a rock crack, the rotation of these cams expands their combined width to match the width of the crack, while maintaining a constant angle against the surface of the rock (relative to the center of the spiral, where force is applied). The pitch angle of the spiral is chosen to optimize the friction of the device against the rock.
*Soft robots based on the logarithmic spiral were designed for scalable and efficient 3D printing. Using cable-driven actuation, they mimic octopus-like movements for stable and versatile object manipulation.
See also
*Archimedean spiral
The Archimedean spiral (also known as Archimedes' spiral, the arithmetic spiral) is a spiral named after the 3rd-century BC Ancient Greece, Greek mathematician Archimedes. The term ''Archimedean spiral'' is sometimes used to refer to the more gene ...
* Epispiral
* List of spirals
* Mice problem, a geometric problem asking for the path followed by mice chasing one another whose solution is a logarithmic spiral
* Tait–Kneser theorem
References
* * Jim WilsonEquiangular Spiral (or Logarithmic Spiral) and Its Related Curves
University of Georgia (1999) * Alexander Bogomolny
Spira Mirabilis - Wonderful Spiral
at cut-the-knot
External links
history and math * *
''SpiralZoom.com''
an educational website about the science of pattern formation, spirals in nature, and spirals in the mythic imagination.
Online exploration using JSXGraph (JavaScript)
YouTube lecture on Zeno's mice problem and logarithmic spirals
{{Spirals Spirals Spiral Spiral Plane curves