Image gradient

An image gradient is a directional change in the intensity or color in an image. The gradient of the image is one of the fundamental building blocks in image processing. For example, the Canny edge detector uses image gradient for edge detection. In graphics software for digital image editing, the term gradient or color gradient is also used for a gradual blend of color which can be considered as an even gradation from low to high values, and seen from black to white in the images to the right. Another name for this is ''color progression''.

Mathematically, the gradient of a two-variable function (here the image intensity function) at each image point is a 2D vector with the components given by the derivatives in the horizontal and vertical directions. At each image point, the gradient vector points in the direction of largest possible intensity increase, and the length of the gradient vector corresponds to the rate of change in that direction.

Since the intensity function of a digital image is only known at discrete points, derivatives of this function cannot be defined unless we assume that there is an underlying continuous intensity function which has been sampled at the image points. With some additional assumptions, the derivative of the continuous intensity function can be computed as a function on the sampled intensity function, i.e., the digital image. Approximations of these derivative functions can be defined at varying degrees of accuracy. The most common way to approximate the image gradient is to convolve an image with a kernel, such as the Sobel operator or Prewitt operator.

Image gradients are often utilized in maps and other visual representations of data in order to convey additional information. GIS tools use color progressions to indicate elevation and population density, among others.

Computer vision

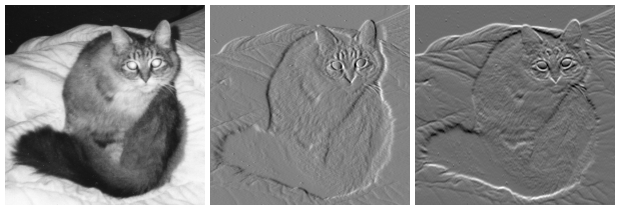
In computer vision, image gradients can be used to extract information from images. Gradient images are created from the original image (generally by convolving with a filter, one of the simplest being the Sobel filter) for this purpose. Each pixel of a gradient image measures the change in intensity of that same point in the original image, in a given direction. To get the full range of direction, gradient images in the x and y directions are computed.

One of the most common uses is in edge detection. After gradient images have been computed, pixels with large gradient values become possible edge pixels. The pixels with the largest gradient values in the direction of the gradient become edge pixels, and edges may be traced in the direction perpendicular to the gradient direction. One example of an edge detection algorithm that uses gradients is the Canny edge detector.

Image gradients can also be used for robust feature and texture matching. Different lighting or camera properties can cause two images of the same scene to have drastically different pixel values. This can cause matching algorithms to fail to match very similar or identical features. One way to solve this is to compute texture or feature signatures based on gradient images computed from the original images. These gradients are less susceptible to lighting and camera changes, so matching errors are reduced.

Mathematics

The gradient of an image is a vector of its partials:

:$\nabla f=\begin g_ \\ g_ \end = \begin \frac \\ \frac \end$,

where:

:$\textstyle\frac$ is the derivative with respect to x (gradient in the x direction)

:$\textstyle\frac$ is the derivative with respect to y (gradient in the y direction).

The derivative of an image can be approximated by finite differences. If central difference is used, to calculate $\textstyle\frac$ we can apply a 1-dimensional filter to the image $\mathbf$ by convolution:

:$\frac = \begin -1 \\ +1 \end * \mathbf$

where $*$ denotes the 1-dimensional convolution operation. This 2×1 filter will shift the image by half a pixel. To avoid this, the following 3×1 filter
:$\begin -1 \\ 0 \\ +1 \end$
can be used. The gradient direction can be calculated by the formula:

:\theta = \operatorname \left \frac \right /math>,

and the magnitude is given by:

:$\sqrt$

See also

*Acutance
* Color banding
* Gradient-domain image processing
* Image derivatives
*Posterization
*Spatial gradient
*Total variation denoising

References

Further reading

*

External links

GradientFilter
function

{{color topics

Computer graphics
Image processing