Horologium Oscillatorium

( English: ''The Pendulum Clock: or Geometrical Demonstrations Concerning the Motion of Pendula as Applied to Clocks'') is a book published by Dutch mathematician and physicist Christiaan Huygens in 1673 and his major work on pendula and horology. It is regarded as one of the three most important works on mechanics in the 17th century, the other two being Galileo’s '' Discourses and Mathematical Demonstrations Relating to Two New Sciences'' (1638) and Newton’s (1687).

Much more than a mere description of clocks, Huygens's is the first modern treatise in which a physical problem (the accelerated motion of a falling body) is idealized by a set of parameters then analyzed mathematically and constitutes one of the seminal works of applied mathematics.Bruce, I. (2007).
Christian Huygens: Horologium Oscillatorium
'. Translated and annotated by Ian Bruce. The book is also known for its strangely worded dedication to Louis XIV.. The appearance of the book in 1673 was a political issue, since at that time the Dutch Republic was at war with France; Huygens was anxious to show his allegiance to his patron, which can be seen in the obsequious dedication to Louis XIV..

Overview

The motivation behind ''Horologium Oscillatorium'' (1673) goes back to the idea of using a pendulum to keep time, which had already been proposed by people engaged in astronomical observations such as Galileo. Mechanical clocks at the time were instead regulated by balances that were often very unreliable.Bos, H. J. M. (1973)
Huygens, Christiaan
''Complete Dictionary of Scientific Biography'', pp. 597-613. Moreover, without reliable clocks, there was no good way to measure longitude at sea, which was particularly problematic for a country dependent on sea trade like the Dutch Republic.

Huygens interest in using a freely suspended pendulum to regulate clocks began in earnest in December 1656. He had a working model by the next year which he patented and then communicated to others such as Frans van Schooten and Claude Mylon.van den Ende, H., Hordijk, B., Kersing, V., & Memel, R. (2018).
The invention of the pendulum clock: A collaboration on the real story
'. Although Huygens’s design, published in a short tract entitled ''Horologium'' (1658), was a combination of existing ideas, it nonetheless became widely popular and many pendulum clocks by Salomon Coster and his associates were built on it. Existing clock towers, such as those at Scheveningen and Utrecht, were also retrofitted following Huygens's design.

Huygens continued his mathematical studies on free fall shortly after and, in 1659, obtained a series of remarkable results. At the same time, he was aware that the periods of simple pendula are not perfectly tautochronous, that is, they do not keep exact time but depend to some extent on their amplitude. Huygens was interested in finding a way to make the bob of a pendulum move reliably and independently of its amplitude. The breakthrough came later that same year when he discovered that the ability to keep perfect time can be achieved if the path of the pendulum bob is a cycloid. However, it was unclear what form to give the metal cheeks regulating the pendulum to lead the bob in a cycloidal path. His famous and surprising solution was that the cheeks must also have the form of a cycloid, on a scale determined by the length of the pendulum.Chareix, F. (2004)
Huygens and mechanics
''Proceedings of the International Conference "Titan - from discovery to encounter" (April 13–17, 2004).'' Noordwijk, Netherlands: ESA Publications Division, , p. 55 - 65. These and other results led Huygens to develop his theory of evolutes and provided the incentive to write a much larger work, which became the ''Horologium Oscillatorium''.

After 1673, during his stay in the '' Academie des Sciences'', Huygens studied harmonic oscillation more generally and continued his attempt at determining longitude at sea using his pendulum clocks, but his experiments carried on ships were not always successful.

Contents

In the Preface, Huygens states:

The book is divided into five interconnected parts. Parts I and V of the book contain descriptions of clock designs. The rest of the book is made of three, highly abstract, mathematical and mechanical parts dealing with pendular motion and a theory of curves. Except for Part IV, written in 1664, the entirety of the book was composed in a three-month period starting in October 1659.

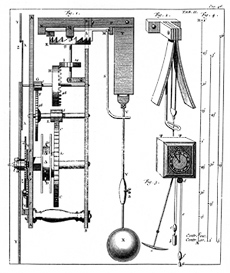
Part I: Description of the oscillating clock

Huygens spends the first part of the book describing in detail his design for an oscillating pendulum clock. It includes descriptions of the endless chain, a lens-shaped bob to reduce air resistance, a small weight to adjust the pendulum swing, an escapement mechanism for connecting the pendulum to the gears, and two thin metal plates in the shape of cycloids mounted on either side to limit pendular motion. This part ends with a table to adjust for the inequality of the solar day, a description on how to draw a cycloid, and a discussion of the application of pendulum clocks for the determination of longitude at sea.

Part II: Fall of weights and motion along a cycloid

In the second part of the book, Huygens states three hypotheses on the motion of bodies, which can be seen as precursors to Newton's three laws of motion. They are essentially the law of inertia, the effect of gravity on uniform motion, and the law of composition of motion:

# If there is no gravity, and the air offers no resistance to the motion of bodies, then any one of these bodies admits of a single motion to be continued with an equal velocity along a straight line.
# Now truly this motion becomes, under the action of gravity and for whatever the direction of the uniform motion, a motion composed from that constant motion that a body now has or had previously, together with the motion due gravity downwards.
# Also, either of these motions can be considered separately, neither one to be impeded by the other.

He uses these three rules to re-derive geometrically Galileo's original study of falling bodies, including linear fall along inclined planes and fall along a curved path. He then studies constrained fall, culminating with a proof that a body falling along an inverted cycloid reaches the bottom in a fixed amount of time, regardless of the point on the path at which it begins to fall. This in effect shows the solution to the tautochrone problem as given by a cycloid curve. In modern notation:

$(\pi/2)\surd(2D/g)$

The following propositions are covered in Part II:

Part III: Size and evolution of the curve

In the third part of the book, Huygens introduces the concept of an evolute as the curve that is "unrolled" (Latin: ''evolutus'') to create a second curve known as the involute. He then uses evolutes to justify the cycloidal shape of the thin plates in Part I. Huygens originally discovered the isochronism of the cycloid using infinitesimal techniques but in his final publication he resorted to proportions and reductio ad absurdum, in the manner of Archimedes, to rectify curves such as the cycloid, the parabola, and other higher order curves.

The following propositions are covered in Part III:

Part IV: Center of oscillation or movement

The fourth and longest part of the book contains the first successful theory of the center of oscillation, together with special methods for applying the theory, and the calculations of the centers of oscillation of several plane and solid figures. Huygens introduces physical parameters into his analysis while addressing the problem of the compound pendulum.

It starts with a number of definitions and proceeds to derive propositions using Torricelli's Principle: ''If some weights begin to move under the force of gravity, then it is not possible for the center of gravity of these weights to ascend to a greater height than that found at the beginning of the motion.'' Huygens called this principle "the chief axiom of mechanics" and used it like a conservation of kinetic energy principle, without recourse to forces or torques. In the process, he obtained solutions to dynamical problems such as the period of an oscillating pendulum as well as a compound pendulum, the center of oscillation and its interchangeability with the pivot point, and the concept of moment of inertia and the constant of gravitational acceleration. Huygens made use, implicitly, of the formula for free fall. In modern notation:

$d = 1/2 gt^2$

The following propositions are covered in Part IV:

Part V: Alternative design and centrifugal force

The last part of the book returns to the design of a clock where the motion of the pendulum is circular, and the string unwinds from the evolute of a parabola. It ends with thirteen propositions regarding bodies in uniform circular motion, without proofs, and states the laws of centrifugal force for uniform circular motion. These propositions were studied closely at the time, although their proofs were only published posthumously in the ''De Vi Centrifuga'' (1703).

Summary

Many of the propositions found in the ''Horologium Oscillatorium'' had little to do with clocks but rather point to the evolution of Huygens’s ideas. When an attempt to measure the gravitational constant using a pendulum failed to give consistent results, Huygens abandoned the experiment and instead idealized the problem into a mathematical study comparing free fall and fall along a circle.

Initially, he followed Galileo’s approach to the study of fall, only to leave it shortly after when it was clear the results could not be extended to curvilinear fall. Huygens then tackled the problem directly by using his own approach to infinitesimal analysis, a combination of analytic geometry, classical geometry, and contemporary infinitesimal techniques. Huygens chose not to publish the majority of his results using these techniques but instead adhered as much as possible to a strictly classical presentation, in the manner of Archimedes.

Legacy

Reception

Initial reviews of Huygens's ''Horologium Oscillatorium'' in major research journals at the time were generally positive. An anonymous review in '' Journal de Sçavans'' (1674) praised the author of the book for his invention of the pendulum clock "which brings the greatest honor to our century because it is of utmost importance... for astronomy and for navigation" while also noting the elegant, but difficult, mathematics needed to fully understand the book. Another review in the '' Giornale de' Letterati'' (1674) repeated many of the same points than the first one, with further elaboration on Huygens's trials at sea. The review in the ''Philosophical Transactions'' (1673) likewise praised the author for his invention but mentions other contributors to the clock design, such as William Neile, that in time would lead to a priority dispute.

In addition to submitting his work for review, Huygens sent copies of his book to individuals throughout Europe, including statesmen such as Johan De Witt, and mathematicians such as Gilles de Roberval and Gregory of St. Vincent. Their appreciation of the text was due not exclusively on their ability to comprehend it fully but rather as a recognition of Huygens’s intellectual standing, or of his gratitude or fraternity that such gift implied. Thus, sending copies of the ''Horologium'' ''Oscillatorium'' worked in a manner similar to a gift of an actual clock, which Huygens had also sent to several people, including Louis XIV and the Grand Duke Ferdinand II.

Mathematical style

Huygens's mathematics in the ''Horologium Oscillatorium'' and elsewhere is best characterized as geometrical analysis of curves and of motions. It closely resembled classical Greek geometry in style, as Huygens preferred the works of classical authors, above all Archimedes. He was also proficient in the analytical geometry of Descartes and Fermat, and made use of it particularly in Parts III and IV of his book. With these and other infinitesimal tools, Huygens was quite capable of finding solutions to hard problems that today are solved using mathematical analysis, such as proving a uniqueness theorem for a class of differential equations, or extending approximation and inequalities techniques to the case of second order differentials.Bos, H. J. M. (1980). Huygens and mathematics. In H.J.M. Bos, M.J.S. Rudwick, H.A.M. Snelders, & R.P.W. Visser (Eds.), ''Studies on Christiaan Huygens'' (pp. 126-146). Swets & Zeitlinger B.V.

Huygens's manner of presentation (i.e., clearly stated axioms, followed by propositions) also made an impression among contemporary mathematicians, including Newton, who studied the propositions on centrifugal force very closely and later acknowledged the influence of ''Horologium Oscillatorium'' on his own major work. Nonetheless, the Archimedean and geometrical style of Huygens's mathematics soon fell into disuse with the advent of the calculus, making it more difficult for subsequent generations to appreciate his work.

Appraisal

Huygens’s most lasting contribution in the ''Horologium Oscillatorium'' is his thorough application of mathematics to explain pendulum clocks, which were the first reliable timekeepers fit for scientific use. His mastery of geometry and physics to design and analyze a precision instrument arguably anticipated the advent of mechanical engineering.

Huygens's analyses of the cycloid in Parts II and III would later lead to the studies of many other such curves, including the caustic, the brachistochrone, the sail curve, and the catenary. Additionally, his exacting mathematical dissection of physical problems into a minimum of parameters provided an example for others (such as the Bernoullis) on work in applied mathematics that would be carry on in the following centuries, albeit in the language of the calculus.

Editions

Huygens’s own manuscript of the book is missing, but he bequeathed his notebooks and correspondence to the Library of the University of Leiden, now in the ''Codices Hugeniorum''. Much of the background material is in ''Oeuvres Complètes'', vols. 17-18.

Since its publication in France in 1673, Huygens’s work has been available in Latin and in the following modern languages:

* First publication. ''Horologium Oscillatorium, Sive De Motu Pendulorum Ad Horologia Aptato Demonstrationes Geometricae''. Latin. Paris: F. Muguet, 1673. 4+ 161 + page


* Later edition by W.J. ’s Gravesande. In ''Christiani Hugenii Zulichemii Opera varia'', 4 vols. Latin. Leiden: J. vander Aa, 1724, 15–192. epr. as ''Christiani Hugenii Zulichemii opera mechanica, geometrica, astronomica et miscellenea'', 4 vols., Leiden: G. Potvliet et alia, 1751
* Standard edition. In ''Oeuvres Complètes'', vol. 18. French and Latin. The Hague: Martinus Nijhoff, 1934, 68–368.
* German translation. ''Die Pendeluhr'' (trans. A. Heckscher and A. von Oettingen), Leipzig: Engelmann, 1913 ( Ostwalds Klassiker der exakten Wissenschaften, no. 192).
* Italian translation. ''L’orologio a pendolo'' (trans. C. Pighetti), Florence: Barbèra, 1963. lso includes an Italian translation of ''Traité de la Lumière''">Traité_de_la_Lumière.html" ;"title="lso includes an Italian translation of ''Traité de la Lumière">lso includes an Italian translation of ''Traité de la Lumière''
* French translation''. L’Horloge oscillante'' (trans. J. Peyroux), Bordeaux: Bergeret, 1980. [Photorepr. Paris: Blanchard, 1980].
* English translation. ''Christiaan Huygens’ The Pendulum Clock, or Geometrical Demonstrations Concerning the Motion Of Pendula As Applied To Clocks'' (trans. R.J. Blackwell), Ames: Iowa State University Press, 1986.
* Dutch translation. ''Christiaan Huygens: Het Slingeruurwerk, een studie'' (transl. J. Aarts), Utrecht: Epsilon Uitgaven, 2015.

References

{{Christiaan Huygens

1673 non-fiction books
1673 in science
17th-century books in Latin
17th-century Dutch books
Physics books
Mathematics books
Mathematics literature
Historical physics publications
Books by Christiaan Huygens
Louis XIV