Gregory's Series on:
[Wikipedia]
[Google]
[Amazon]
In mathematics, the arctangent series, traditionally called Gregory's series, is the
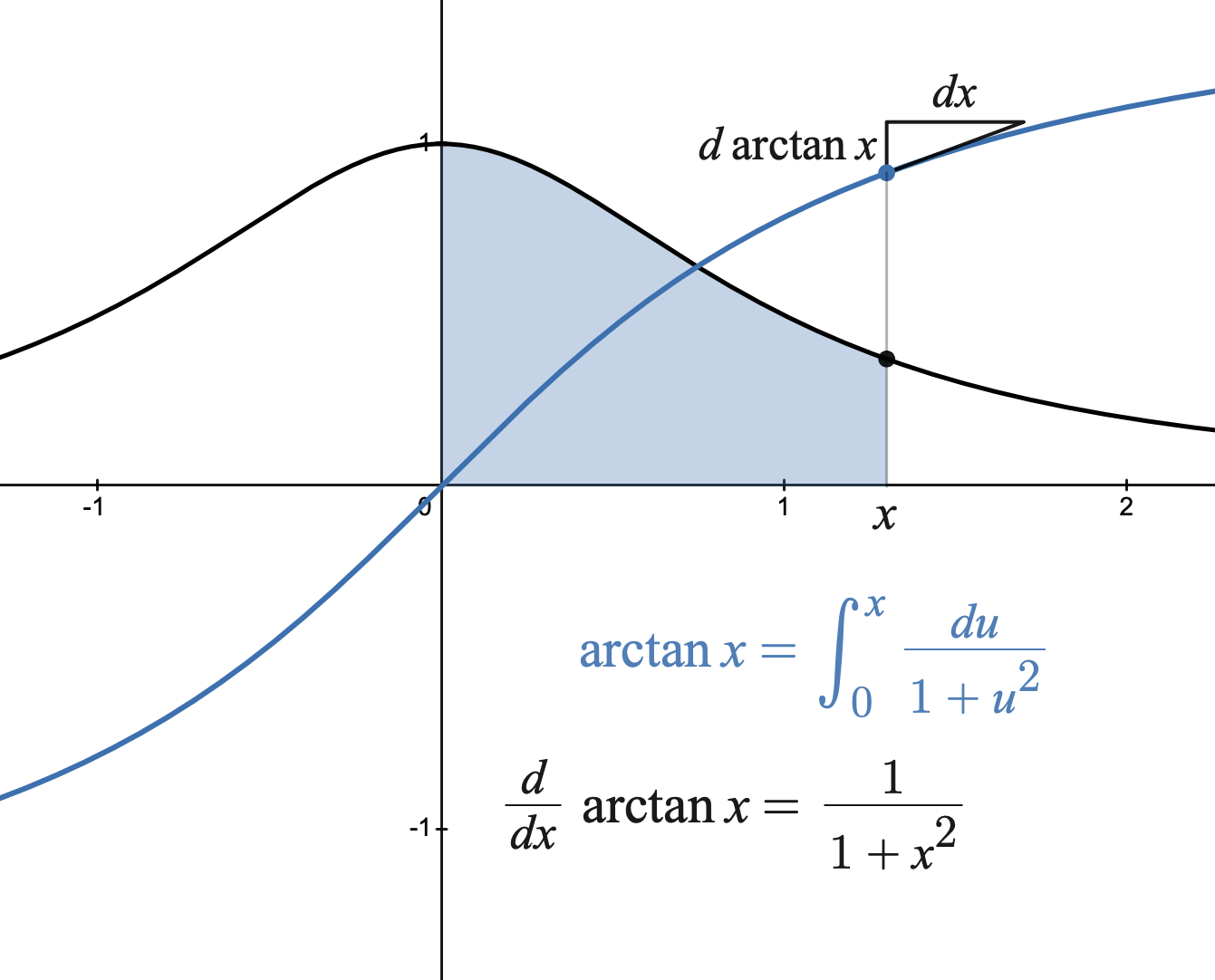 If then The derivative is
:
Taking the reciprocal,
:
This sometimes is used as a definition of the arctangent:
:
The
If then The derivative is
:
Taking the reciprocal,
:
This sometimes is used as a definition of the arctangent:
:
The
Taylor series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor ser ...
expansion at the origin of the arctangent function:
:
This series converges in the complex
Complex commonly refers to:
* Complexity, the behaviour of a system whose components interact in multiple ways so possible interactions are difficult to describe
** Complex system, a system composed of many components which may interact with each ...
disk except for (where
It was first discovered in the 14th century by Indian mathematician
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics (400 CE to 1200 CE), important contributions were made by scholars like Aryabhata, Brahmagupta, ...
Mādhava of Sangamagrāma ( – c. 1425), the founder of the Kerala school, and is described in extant works by Nīlakaṇṭha Somayāji (c. 1500) and Jyeṣṭhadeva
Jyeṣṭhadeva () was an astronomer-mathematician of the Kerala school of astronomy and mathematics founded by Madhava of Sangamagrama (). He is best known as the author of '' Yuktibhāṣā'', a commentary in Malayalam of Tantrasamgraha by ...
(c. 1530). Mādhava's work was unknown in Europe, and the arctangent series was independently rediscovered by James Gregory in 1671 and by Gottfried Leibniz
Gottfried Wilhelm Leibniz (or Leibnitz; – 14 November 1716) was a German polymath active as a mathematician, philosopher, scientist and diplomat who is credited, alongside Isaac Newton, Sir Isaac Newton, with the creation of calculus in ad ...
in 1673. In recent literature the arctangent series is sometimes called the Mādhava–Gregory series to recognize Mādhava's priority (see also Mādhava series).
The special case of the arctangent of is traditionally called the ''Leibniz formula'' for , or recently sometimes the ''Mādhava–Leibniz formula'':
:
The extremely slow convergence of the arctangent series for makes this formula impractical per se. Kerala-school mathematicians used additional correction terms to speed convergence. John Machin (1706) expressed as a sum of arctangents of smaller values, eventually resulting in a variety of Machin-like formulas for . Isaac Newton
Sir Isaac Newton () was an English polymath active as a mathematician, physicist, astronomer, alchemist, theologian, and author. Newton was a key figure in the Scientific Revolution and the Age of Enlightenment, Enlightenment that followed ...
(1684) and other mathematicians accelerated the convergence of the series via various transformations.
Proof
 If then The derivative is
:
Taking the reciprocal,
:
This sometimes is used as a definition of the arctangent:
:
The
If then The derivative is
:
Taking the reciprocal,
:
This sometimes is used as a definition of the arctangent:
:
The Maclaurin series
Maclaurin or MacLaurin is a surname. Notable people with the surname include:
* Colin Maclaurin (1698–1746), Scottish mathematician
* Normand MacLaurin (1835–1914), Australian politician and university administrator
* Henry Normand MacLaurin ...
for is a geometric series
In mathematics, a geometric series is a series (mathematics), series summing the terms of an infinite geometric sequence, in which the ratio of consecutive terms is constant. For example, 1/2 + 1/4 + 1/8 + 1/16 + ⋯, the series \tfrac12 + \tfrac1 ...
:
:
One can find the Maclaurin series for by naïvely integrating term-by-term:
:
While this turns out correctly, integrals and infinite sums cannot always be exchanged in this manner. To prove that the integral on the left converges to the sum on the right for real can instead be written as the ''finite'' sum,
:
Again integrating both sides,
:
In the limit as the integral on the right above tends to zero when because
:
Therefore,
:
Convergence
The series for and converge within the complex disk , where both functions areholomorphic
In mathematics, a holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighbourhood of each point in a domain in complex coordinate space . The existence of a complex deri ...
. They diverge for because when , there is a pole:
:
When the partial sums alternate between the values and never converging to the value
However, its term-by-term integral, the series for (barely) converges when because disagrees with its series only at the point so the difference in integrals can be made arbitrarily small by taking sufficiently many terms:
:
Because of its exceedingly slow convergence (it takes five billion terms to obtain 10 correct decimal digits), the Leibniz formula is not a very effective practical method for computing Finding ways to get around this slow convergence has been a subject of great mathematical interest.
Accelerated series
Isaac Newton
Sir Isaac Newton () was an English polymath active as a mathematician, physicist, astronomer, alchemist, theologian, and author. Newton was a key figure in the Scientific Revolution and the Age of Enlightenment, Enlightenment that followed ...
accelerated the convergence of the arctangent series in 1684 (in an unpublished work; others independently discovered the result and it was later popularized by Leonhard Euler
Leonhard Euler ( ; ; ; 15 April 170718 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential ...
's 1755 textbook; Euler wrote two proofs in 1779), yielding a series converging for
:
where and
Each term of this modified series is a rational function
In mathematics, a rational function is any function that can be defined by a rational fraction, which is an algebraic fraction such that both the numerator and the denominator are polynomials. The coefficients of the polynomials need not be ...
with its poles
Pole or poles may refer to:
People
*Poles (people), another term for Polish people, from the country of Poland
* Pole (surname), including a list of people with the name
* Pole (musician) (Stefan Betke, born 1967), German electronic music artist
...
at in the complex plane
In mathematics, the complex plane is the plane (geometry), plane formed by the complex numbers, with a Cartesian coordinate system such that the horizontal -axis, called the real axis, is formed by the real numbers, and the vertical -axis, call ...
, the same place where the arctangent function has its poles. By contrast, a polynomial such as the Taylor series for arctangent forces all of its poles to infinity.
History
The earliest person to whom the series can be attributed with confidence is Mādhava of Sangamagrāma (c. 1340 – c. 1425). The original reference (as with much of Mādhava's work) is lost, but he is credited with the discovery by several of his successors in theKerala school of astronomy and mathematics
The Kerala school of astronomy and mathematics or the Kerala school was a school of Indian mathematics, mathematics and Indian astronomy, astronomy founded by Madhava of Sangamagrama in Kingdom of Tanur, Tirur, Malappuram district, Malappuram, K ...
founded by him. Specific citations to the series for include Nīlakaṇṭha Somayāji's '' Tantrasaṅgraha'' (c. 1500),
Jyeṣṭhadeva
Jyeṣṭhadeva () was an astronomer-mathematician of the Kerala school of astronomy and mathematics founded by Madhava of Sangamagrama (). He is best known as the author of '' Yuktibhāṣā'', a commentary in Malayalam of Tantrasamgraha by ...
's ''Yuktibhāṣā
''Yuktibhāṣā'' (), also known as Gaṇita-yukti-bhāṣā and ( English: ''Compendium of Astronomical Rationale''), is a major treatise on mathematics and astronomy, written by the Indian astronomer Jyesthadeva of the Kerala school of mat ...
'' (c. 1530), and the ''Yukti-dipika'' commentary by Sankara Variyar, where it is given in verses 2.206 – 2.209.
See also
*List of mathematical series
This list of mathematical series contains formulae for finite and infinite sums. It can be used in conjunction with other tools for evaluating sums.
*Here, 0^0 Zero to the power of zero, is taken to have the value 1
*\ denotes the fractional part ...
* Mādhava series
Notes
References
* * * * * {{cite journal , last = Roy , first = Ranjan , year = 1990 , title = The Discovery of the Series Formula for {{mvar , π by Leibniz, Gregory and Nilakantha , journal = Mathematics Magazine , volume = 63 , number = 5 , pages = 291–306 , url = https://www.maa.org/sites/default/files/images/upload_library/22/Allendoerfer/1991/0025570x.di021167.02p0073q.pdf , doi = 10.1080/0025570X.1990.11977541 Series (mathematics)