Flight dynamics (spacecraft) on:
[Wikipedia]
[Google]
[Amazon]
 Spacecraft flight dynamics is the application of mechanical dynamics to
Spacecraft flight dynamics is the application of mechanical dynamics to
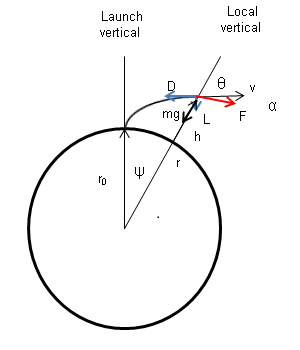 The general case of a launch from Earth must take engine thrust, aerodynamic forces, and gravity into account. The acceleration equation can be reduced from vector to scalar form by resolving it into its tangential (speed ) and angular (flight path angle relative to local vertical) time rate-of-change components relative to the launch pad. The two equations thus become:
:
:
where:
:''F'' is the engine thrust;
:''α'' is the angle of attack;
:''m'' is the vehicle's mass;
:''D'' is the vehicle's aerodynamic drag;
:''L'' is its
The general case of a launch from Earth must take engine thrust, aerodynamic forces, and gravity into account. The acceleration equation can be reduced from vector to scalar form by resolving it into its tangential (speed ) and angular (flight path angle relative to local vertical) time rate-of-change components relative to the launch pad. The two equations thus become:
:
:
where:
:''F'' is the engine thrust;
:''α'' is the angle of attack;
:''m'' is the vehicle's mass;
:''D'' is the vehicle's aerodynamic drag;
:''L'' is its  :
:
:
The planet-fixed values of ''v'' and ''θ'' are converted to space-fixed (inertial) values with the following conversions:
:
where ''ω'' is the planet's rotational rate in radians per second, ''φ'' is the launch site latitude, and ''A''''z'' is the launch
:
:
:
The planet-fixed values of ''v'' and ''θ'' are converted to space-fixed (inertial) values with the following conversions:
:
where ''ω'' is the planet's rotational rate in radians per second, ''φ'' is the launch site latitude, and ''A''''z'' is the launch
 The orientation of the orbit in space is specified by three angles:
*The ''inclination'' ''i'', of the orbital plane with the fundamental plane (this is usually a planet or moon's equatorial plane, or in the case of a solar orbit, the Earth's orbital plane around the Sun, known as the
The orientation of the orbit in space is specified by three angles:
*The ''inclination'' ''i'', of the orbital plane with the fundamental plane (this is usually a planet or moon's equatorial plane, or in the case of a solar orbit, the Earth's orbital plane around the Sun, known as the
 A
A
 A slightly more complicated altitude change maneuver is the
A slightly more complicated altitude change maneuver is the
 Vehicles sent on lunar or planetary missions are generally not launched by direct injection to departure trajectory, but first put into a low Earth
Vehicles sent on lunar or planetary missions are generally not launched by direct injection to departure trajectory, but first put into a low Earth
 Spacecraft flight dynamics is the application of mechanical dynamics to
Spacecraft flight dynamics is the application of mechanical dynamics to model
A model is an informative representation of an object, person or system. The term originally denoted the plans of a building in late 16th-century English, and derived via French and Italian ultimately from Latin ''modulus'', a measure.
Models c ...
how the external forces acting on a space vehicle
A space vehicle is the combination of a spacecraft and its launch vehicle which carries it into space. The earliest space vehicles were expendable launch systems, using a single or multistage rocket to carry a relatively small spacecraft in p ...
or spacecraft
A spacecraft is a vehicle or machine designed to spaceflight, fly in outer space. A type of artificial satellite, spacecraft are used for a variety of purposes, including Telecommunications, communications, Earth observation satellite, Earth ...
determine its flight path. These forces are primarily of three types: propulsive
A prokinetic agent (also gastroprokinetic agent, gastrokinetic agent or propulsive) is a type of drug which enhances gastrointestinal motility by increasing the frequency or strength of contractions, but without disrupting their rhythm. They are u ...
force provided by the vehicle's engines; gravitational force exerted by the Earth and other celestial bodies; and aerodynamic lift and drag (when flying in the atmosphere of the Earth or other body, such as Mars or Venus).
The principles of flight dynamics are used to model a vehicle's powered flight during launch from the Earth; a spacecraft's orbital flight; maneuvers to change orbit; translunar and interplanetary flight; launch from and landing on a celestial body, with or without an atmosphere; entry through the atmosphere of the Earth or other celestial body; and attitude control
Attitude control is the process of controlling the orientation of an aerospace vehicle with respect to an inertial frame of reference or another entity such as the celestial sphere, certain fields, and nearby objects, etc.
Controlling vehicle ...
. They are generally programmed into a vehicle's inertial navigation system
An inertial navigation system (INS) is a navigation device that uses motion sensors ( accelerometers), rotation sensors (gyroscopes) and a computer to continuously calculate by dead reckoning the position, the orientation, and the velocity (d ...
s, and monitored on the ground by a member of the flight controller
Flight controllers are personnel who aid space flight by working in such Mission Control Centers as NASA's Mission Control Center or ESA's European Space Operations Centre. Flight controllers work at computer consoles and use telemetry to m ...
team known in NASA
The National Aeronautics and Space Administration (NASA ) is an independent agency of the US federal government responsible for the civil space program, aeronautics research, and space research.
NASA was established in 1958, succeedi ...
as the flight dynamics officer
Flight controllers are personnel who aid space flight by working in such Mission Control Centers as NASA's Mission Control Center or ESA's European Space Operations Centre. Flight controllers work at computer consoles and use telemetry t ...
, or in the European Space Agency
, owners =
, headquarters = Paris, Île-de-France, France
, coordinates =
, spaceport = Guiana Space Centre
, seal = File:ESA emblem seal.png
, seal_size = 130px
, image = Views in the Main Control Room (120 ...
as the spacecraft navigator.
Flight dynamics depends on the disciplines of propulsion, aerodynamics
Aerodynamics, from grc, ἀήρ ''aero'' (air) + grc, δυναμική (dynamics), is the study of the motion of air, particularly when affected by a solid object, such as an airplane wing. It involves topics covered in the field of fluid dyn ...
, and astrodynamics (orbital mechanics
Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets and other spacecraft. The motion of these objects is usually calculated from Newton's laws of ...
and celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of objects in outer space. Historically, celestial mechanics applies principles of physics (classical mechanics) to astronomical objects, such as stars and planets, to ...
). It cannot be reduced to simply attitude control; real spacecraft do not have steering wheels or tillers like airplanes or ships. Unlike the way fictional spaceships are portrayed, a spacecraft actually does not bank to turn in outer space, where its flight path depends strictly on the gravitational forces acting on it and the propulsive maneuvers applied.
Basic principles
Aspace vehicle
A space vehicle is the combination of a spacecraft and its launch vehicle which carries it into space. The earliest space vehicles were expendable launch systems, using a single or multistage rocket to carry a relatively small spacecraft in p ...
's flight is determined by application of Newton
Newton most commonly refers to:
* Isaac Newton (1642–1726/1727), English scientist
* Newton (unit), SI unit of force named after Isaac Newton
Newton may also refer to:
Arts and entertainment
* ''Newton'' (film), a 2017 Indian film
* Newton ( ...
's second law of motion
Newton's laws of motion are three basic laws of classical mechanics that describe the relationship between the motion of an object and the forces acting on it. These laws can be paraphrased as follows:
# A body remains at rest, or in motion ...
:
:
where F is the vector
Vector most often refers to:
*Euclidean vector, a quantity with a magnitude and a direction
*Vector (epidemiology), an agent that carries and transmits an infectious pathogen into another living organism
Vector may also refer to:
Mathematic ...
sum of all forces exerted on the vehicle, m is its current mass, and a is the acceleration vector, the instantaneous rate of change of velocity (v), which in turn is the instantaneous rate of change of displacement. Solving for a, acceleration equals the force sum divided by mass. Acceleration is integrated over time to get velocity, and velocity is in turn integrated to get position.
Flight dynamics calculations are handled by computerized guidance system
A guidance system is a virtual or physical device, or a group of devices implementing a controlling the movement of a ship, aircraft, missile, rocket, satellite, or any other moving object. Guidance is the process of calculating the changes ...
s aboard the vehicle; the status of the flight dynamics is monitored on the ground during powered maneuvers by a member of the flight controller
Flight controllers are personnel who aid space flight by working in such Mission Control Centers as NASA's Mission Control Center or ESA's European Space Operations Centre. Flight controllers work at computer consoles and use telemetry to m ...
team known in NASA
The National Aeronautics and Space Administration (NASA ) is an independent agency of the US federal government responsible for the civil space program, aeronautics research, and space research.
NASA was established in 1958, succeedi ...
's Human Spaceflight Center as the flight dynamics officer
Flight controllers are personnel who aid space flight by working in such Mission Control Centers as NASA's Mission Control Center or ESA's European Space Operations Centre. Flight controllers work at computer consoles and use telemetry t ...
, or in the European Space Agency
, owners =
, headquarters = Paris, Île-de-France, France
, coordinates =
, spaceport = Guiana Space Centre
, seal = File:ESA emblem seal.png
, seal_size = 130px
, image = Views in the Main Control Room (120 ...
as the spacecraft navigator.
For powered atmospheric flight, the three main forces which act on a vehicle are propulsive force, aerodynamic force
In fluid mechanics, an aerodynamic force is a force exerted on a body by the air (or other gas) in which the body is immersed, and is due to the relative motion between the body and the gas.
Force
There are two causes of aerodynamic force:
...
, and gravitation. Other external forces such as centrifugal force
In Newtonian mechanics, the centrifugal force is an inertial force (also called a "fictitious" or "pseudo" force) that appears to act on all objects when viewed in a rotating frame of reference. It is directed away from an axis which is parallel ...
, Coriolis force
In physics, the Coriolis force is an inertial or fictitious force that acts on objects in motion within a frame of reference that rotates with respect to an inertial frame. In a reference frame with clockwise rotation, the force acts to the ...
, and solar radiation pressure
Radiation pressure is the mechanical pressure exerted upon any surface due to the exchange of momentum between the object and the electromagnetic field. This includes the momentum of light or electromagnetic radiation of any wavelength that is a ...
are generally insignificant due to the relatively short time of powered flight and small size of spacecraft, and may generally be neglected in simplified performance calculations.
Propulsion
The thrust of arocket engine
A rocket engine uses stored rocket propellants as the reaction mass for forming a high-speed propulsive Jet (fluid), jet of fluid, usually high-temperature gas. Rocket engines are reaction engines, producing thrust by ejecting mass rearward, i ...
, in the general case of operation in an atmosphere, is approximated by: See Equation 2-14.
:
:
The effective exhaust velocity of the rocket propellant is proportional to the vacuum specific impulse
Specific impulse (usually abbreviated ) is a measure of how efficiently a reaction mass engine (a rocket using propellant or a jet engine using fuel) creates thrust. For engines whose reaction mass is only the fuel they carry, specific impulse is ...
and affected by the atmospheric pressure:
:
where:
: has units of seconds
: is the gravitational acceleration at the surface of the Earth
The specific impulse relates the delta-v
Delta-''v'' (more known as " change in velocity"), symbolized as ∆''v'' and pronounced ''delta-vee'', as used in spacecraft flight dynamics, is a measure of the impulse per unit of spacecraft mass that is needed to perform a maneuver such ...
capacity to the quantity of propellant consumed according to the Tsiolkovsky rocket equation
Konstantin Eduardovich Tsiolkovsky (russian: Константи́н Эдуа́рдович Циолко́вский , , p=kənstɐnʲˈtʲin ɪdʊˈardəvʲɪtɕ tsɨɐlˈkofskʲɪj , a=Ru-Konstantin Tsiolkovsky.oga; – 19 September 1935) ...
:
:
where:
: is the initial total mass, including propellant, in kg (or lb)
: is the final total mass in kg (or lb)
: is the effective exhaust velocity in m/s (or ft/s)
: is the delta-v in m/s (or ft/s)
Aerodynamic force
Aerodynamic force
In fluid mechanics, an aerodynamic force is a force exerted on a body by the air (or other gas) in which the body is immersed, and is due to the relative motion between the body and the gas.
Force
There are two causes of aerodynamic force:
...
s, present near a body with significant atmosphere such as Earth
Earth is the third planet from the Sun and the only astronomical object known to harbor life. While large volumes of water can be found throughout the Solar System, only Earth sustains liquid surface water. About 71% of Earth's surf ...
, Mars
Mars is the fourth planet from the Sun and the second-smallest planet in the Solar System, only being larger than Mercury. In the English language, Mars is named for the Roman god of war. Mars is a terrestrial planet with a thin atmos ...
or Venus
Venus is the second planet from the Sun. It is sometimes called Earth's "sister" or "twin" planet as it is almost as large and has a similar composition. As an interior planet to Earth, Venus (like Mercury) appears in Earth's sky never f ...
, are analyzed as: lift
Lift or LIFT may refer to:
Physical devices
* Elevator, or lift, a device used for raising and lowering people or goods
** Paternoster lift, a type of lift using a continuous chain of cars which do not stop
** Patient lift, or Hoyer lift, mobile ...
, defined as the force component perpendicular to the direction of flight (not necessarily upward to balance gravity, as for an airplane); and drag
Drag or The Drag may refer to:
Places
* Drag, Norway, a village in Tysfjord municipality, Nordland, Norway
* ''Drág'', the Hungarian name for Dragu Commune in Sălaj County, Romania
* Drag (Austin, Texas), the portion of Guadalupe Street adj ...
, the component parallel to, and in the opposite direction of flight. Lift and drag are modeled as the products of a coefficient times dynamic pressure
In fluid dynamics, dynamic pressure (denoted by or and sometimes called velocity pressure) is the quantity defined by:Clancy, L.J., ''Aerodynamics'', Section 3.5
:q = \frac\rho\, u^2
where (in SI units):
* is the dynamic pressure in pascals ...
acting on a reference area:
:
:
where:
*''C''''L'' is roughly linear with ''α'', the angle of attack between the vehicle axis and the direction of flight (up to a limiting value), and is 0 at ''α'' = 0 for an axisymmetric body;
*''C''''D'' varies with ''α''2;
*''C''''L'' and ''C''''D'' vary with Reynolds number and Mach number
Mach number (M or Ma) (; ) is a dimensionless quantity in fluid dynamics representing the ratio of flow velocity past a boundary to the local speed of sound.
It is named after the Moravian physicist and philosopher Ernst Mach.
: \mathrm = \ ...
;
*''q'', the dynamic pressure, is equal to 1/2 ''ρv''2, where ''ρ'' is atmospheric density, modeled for Earth as a function of altitude in the International Standard Atmosphere
The International Standard Atmosphere (ISA) is a static atmospheric model of how the pressure, temperature, density, and viscosity of the Earth's atmosphere change over a wide range of altitudes or elevations. It has been established to provide ...
(using an assumed temperature distribution, hydrostatic pressure
Fluid statics or hydrostatics is the branch of fluid mechanics that studies the condition of the equilibrium of a floating body and submerged body " fluids at hydrostatic equilibrium and the pressure in a fluid, or exerted by a fluid, on an i ...
variation, and the ideal gas law
The ideal gas law, also called the general gas equation, is the equation of state of a hypothetical ideal gas. It is a good approximation of the behavior of many gases under many conditions, although it has several limitations. It was first st ...
); and
*''A''ref is a characteristic area of the vehicle, such as cross-sectional area at the maximum diameter.
Gravitation
The gravitational force that a celestial body exerts on a space vehicle is modeled with the body and vehicle taken as point masses; the bodies (Earth, Moon, etc.) are simplified as spheres; and the mass of the vehicle is much smaller than the mass of the body so that its effect on the gravitational acceleration can be neglected. Therefore the gravitational force is calculated by: : where: : is the gravitational force (weight); : is the space vehicle's mass; and : is the radial distance of the vehicle to the planet's center; and : is the radial distance from the planet's surface to its center; and : is thegravitational acceleration
In physics, gravitational acceleration is the acceleration of an object in free fall within a vacuum (and thus without experiencing drag (physics), drag). This is the steady gain in speed caused exclusively by the force of gravitational attract ...
at the surface of the planet
:''g'' is the gravitational acceleration
In physics, gravitational acceleration is the acceleration of an object in free fall within a vacuum (and thus without experiencing drag (physics), drag). This is the steady gain in speed caused exclusively by the force of gravitational attract ...
at altitude, which varies with the inverse square of the radial distance to the planet's center:
::
Powered flight
The equations of motion used to describe powered flight of a vehicle during launch can be as complex as sixdegrees of freedom
Degrees of freedom (often abbreviated df or DOF) refers to the number of independent variables or parameters of a thermodynamic system. In various scientific fields, the word "freedom" is used to describe the limits to which physical movement or ...
for in-flight calculations, or as simple as two degrees of freedom for preliminary performance estimates. In-flight calculations will take perturbation factors into account such as the Earth's oblateness
Flattening is a measure of the compression of a circle or sphere along a diameter to form an ellipse or an ellipsoid of revolution (spheroid) respectively. Other terms used are ellipticity, or oblateness. The usual notation for flattening is ...
and non-uniform mass distribution; and gravitational forces of all nearby bodies, including the Moon, Sun, and other planets. Preliminary estimates can make some simplifying assumptions: a spherical, uniform planet; the vehicle can be represented as a point mass; solution of the flight path presents a two-body problem
In classical mechanics, the two-body problem is to predict the motion of two massive objects which are abstractly viewed as point particles. The problem assumes that the two objects interact only with one another; the only force affecting each ...
; and the local flight path lies in a single plane) with reasonably small loss of accuracy.
 The general case of a launch from Earth must take engine thrust, aerodynamic forces, and gravity into account. The acceleration equation can be reduced from vector to scalar form by resolving it into its tangential (speed ) and angular (flight path angle relative to local vertical) time rate-of-change components relative to the launch pad. The two equations thus become:
:
:
where:
:''F'' is the engine thrust;
:''α'' is the angle of attack;
:''m'' is the vehicle's mass;
:''D'' is the vehicle's aerodynamic drag;
:''L'' is its
The general case of a launch from Earth must take engine thrust, aerodynamic forces, and gravity into account. The acceleration equation can be reduced from vector to scalar form by resolving it into its tangential (speed ) and angular (flight path angle relative to local vertical) time rate-of-change components relative to the launch pad. The two equations thus become:
:
:
where:
:''F'' is the engine thrust;
:''α'' is the angle of attack;
:''m'' is the vehicle's mass;
:''D'' is the vehicle's aerodynamic drag;
:''L'' is its aerodynamic lift
A fluid flowing around an object exerts a force on it. Lift is the component of this force that is perpendicular to the oncoming flow direction. It contrasts with the drag force, which is the component of the force parallel to the flow directi ...
;
:''r'' is the radial distance to the planet's center; and
:''g'' is the gravitational acceleration
In physics, gravitational acceleration is the acceleration of an object in free fall within a vacuum (and thus without experiencing drag (physics), drag). This is the steady gain in speed caused exclusively by the force of gravitational attract ...
at altitude.
Mass decreases as propellant is consumed and rocket stages
A rocket (from it, rocchetto, , bobbin/spool) is a vehicle that uses jet propulsion to accelerate without using the surrounding air. A rocket engine produces thrust by reaction to exhaust expelled at high speed. Rocket engines work entirely fr ...
, engines or tanks are shed (if applicable).
The planet-fixed values of v and θ at any time in the flight are then determined by numerical integration
In analysis, numerical integration comprises a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations ...
of the two rate equations from time zero (when both ''v'' and ''θ'' are 0):
:
:
Finite element analysis
The finite element method (FEM) is a popular method for numerically solving differential equations arising in engineering and mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat t ...
can be used to integrate the equations, by breaking the flight into small time increments.
For most launch vehicle
A launch vehicle or carrier rocket is a rocket designed to carry a payload (spacecraft or satellites) from the Earth's surface to outer space. Most launch vehicles operate from a launch pads, supported by a launch control center and syste ...
s, relatively small levels of lift are generated, and a gravity turn
In physics, gravity () is a fundamental interaction which causes mutual attraction between all things with mass or energy. Gravity is, by far, the weakest of the four fundamental interactions, approximately 1038 times weaker than the strong ...
is employed, depending mostly on the third term of the angle rate equation. At the moment of liftoff, when angle and velocity are both zero, the theta-dot equation is mathematically indeterminate and cannot be evaluated until velocity becomes non-zero shortly after liftoff. But notice at this condition, the only force which can cause the vehicle to pitch over is the engine thrust acting at a non-zero angle of attack (first term) and perhaps a slight amount of lift (second term), until a non-zero pitch angle is attained. In the gravity turn, pitch-over is initiated by applying an increasing angle of attack (by means of gimbaled engine thrust), followed by a gradual decrease in angle of attack through the remainder of the flight.
Once velocity and flight path angle are known, altitude and downrange distance are computed as:
azimuth
An azimuth (; from ar, اَلسُّمُوت, as-sumūt, the directions) is an angular measurement in a spherical coordinate system. More specifically, it is the horizontal angle from a cardinal direction, most commonly north.
Mathematicall ...
angle.
:
Final ''v''''s'', ''θ''''s'' and ''r'' must match the requirements of the target orbit as determined by orbital mechanics (see Orbital flight
An orbital spaceflight (or orbital flight) is a spaceflight in which a spacecraft is placed on a trajectory where it could remain in space for at least one orbit. To do this around the Earth, it must be on a free trajectory which has an altit ...
, above), where final ''v''''s'' is usually the required periapsis (or circular) velocity, and final ''θ''''s'' is 90 degrees. A powered descent analysis would use the same procedure, with reverse boundary conditions.
Orbital flight
Orbital mechanics are used to calculate flight in orbit about a central body. For sufficiently high orbits (generally at least in the case of Earth), aerodynamic force may be assumed to be negligible for relatively short term missions (though a small amount of drag may be present which results in decay of orbital energy over longer periods of time.) When the central body's mass is much larger than the spacecraft, and other bodies are sufficiently far away, the solution of orbital trajectories can be treated as a two-body problem. This can be shown to result in the trajectory being ideally aconic section
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a ...
(circle, ellipse, parabola or hyperbola) with the central body located at one focus. Orbital trajectories are either circles or ellipses; the parabolic trajectory represents first escape of the vehicle from the central body's gravitational field. Hyperbolic trajectories are escape trajectories with excess velocity, and will be covered under Interplanetary flight
''Interplanetary Flight: An Introduction to Astronautics'Interplanetary Flight: An Introduction to Astronautics''. London: Temple Press, 1950 is a short, modestly technical introduction to space exploration written by Arthur C. Clarke, an ...
below.
Elliptical orbits are characterized by three elements. The semi-major axis ''a'' is the average of the radius at apoapsis and periapsis:
:
The eccentricity
Eccentricity or eccentric may refer to:
* Eccentricity (behavior), odd behavior on the part of a person, as opposed to being "normal"
Mathematics, science and technology Mathematics
* Off- center, in geometry
* Eccentricity (graph theory) of a ...
''e'' can then be calculated for an ellipse, knowing the apses:
:
The time period for a complete orbit is dependent only on the semi-major axis, and is independent of eccentricity:
:
where is the standard gravitational parameter
In celestial mechanics, the standard gravitational parameter ''μ'' of a celestial body is the product of the gravitational constant ''G'' and the mass ''M'' of the bodies. For two bodies the parameter may be expressed as G(m1+m2), or as GM when ...
of the central body.
ecliptic
The ecliptic or ecliptic plane is the orbital plane of the Earth around the Sun. From the perspective of an observer on Earth, the Sun's movement around the celestial sphere over the course of a year traces out a path along the ecliptic agai ...
.) Positive inclination is northward, while negative inclination is southward.
*The ''longitude of the ascending node'' Ω, measured in the fundamental plane counter-clockwise looking southward, from a reference direction (usually the vernal equinox Spring equinox or vernal equinox or variations may refer to:
* March equinox, the spring equinox in the Northern Hemisphere
* September equinox, the spring equinox in the Southern Hemisphere
Other uses
* Nowruz, Persian/Iranian new year which be ...
) to the line where the spacecraft crosses this plane from south to north. (If inclination is zero, this angle is undefined and taken as 0.)
*The ''argument of periapsis'' ''ω'', measured in the orbital plane counter-clockwise looking southward, from the ascending node to the periapsis. If the inclination is 0, there is no ascending node, so ''ω'' is measured from the reference direction. For a circular orbit, there is no periapsis, so ''ω'' is taken as 0.
The orbital plane is ideally constant, but is usually subject to small perturbations caused by planetary oblateness and the presence of other bodies.
The spacecraft's position in orbit is specified by the ''true anomaly,'' , an angle measured from the periapsis, or for a circular orbit, from the ascending node or reference direction. The ''semi-latus rectum'', or radius at 90 degrees from periapsis, is:
:
The radius at any position in flight is:
:
and the velocity at that position is:
:
Types of orbit
Circular
For a circular orbit, ''r''''a'' = ''r''''p'' = ''a'', and eccentricity is 0. Circular velocity at a given radius is: :Elliptical
For an elliptical orbit, ''e'' is greater than 0 but less than 1. The periapsis velocity is: : and the apoapsis velocity is: : The limiting condition is a parabolic escape orbit, when ''e'' = 1 and ''r''''a'' becomes infinite. Escape velocity at periapsis is then :Flight path angle
The ''specific angular momentum'' of any conic orbit, ''h'', is constant, and is equal to the product of radius and velocity at periapsis. At any other point in the orbit, it is equal to: : where ''φ'' is the flight path angle measured from the local horizontal (perpendicular to ''r''.) This allows the calculation of ''φ'' at any point in the orbit, knowing radius and velocity: : Note that flight path angle is a constant 0 degrees (90 degrees from local vertical) for a circular orbit.True anomaly as a function of time
It can be shown that the angular momentum equation given above also relates the rate of change in true anomaly to ''r'', ''v'', and ''φ'', thus the true anomaly can be found as a function of time since periapsis passage by integration: : Conversely, the time required to reach a given anomaly is: :Orbital maneuvers
Once in orbit, a spacecraft may fire rocket engines to make in-plane changes to a different altitude or type of orbit, or to change its orbital plane. These maneuvers require changes in the craft's velocity, and theclassical rocket equation
Classical may refer to:
European antiquity
*Classical antiquity, a period of history from roughly the 7th or 8th century B.C.E. to the 5th century C.E. centered on the Mediterranean Sea
*Classical architecture, architecture derived from Greek and ...
is used to calculate the propellant requirements for a given delta-v
Delta-''v'' (more known as " change in velocity"), symbolized as ∆''v'' and pronounced ''delta-vee'', as used in spacecraft flight dynamics, is a measure of the impulse per unit of spacecraft mass that is needed to perform a maneuver such ...
. A delta-''v'' budget will add up all the propellant requirements, or determine the total delta-v available from a given amount of propellant, for the mission. Most on-orbit maneuvers can be modeled as impulsive, that is as a near-instantaneous change in velocity, with minimal loss of accuracy.
In-plane changes
=Orbit circularization
= An elliptical orbit is most easily converted to a circular orbit at the periapsis or apoapsis by applying a single engine burn with a delta v equal to the difference between the desired orbit's circular velocity and the current orbit's periapsis or apoapsis velocity: To circularize at periapsis, a retrograde burn is made: : To circularize at apoapsis, a posigrade burn is made: :=Altitude change by Hohmann transfer
=Hohmann transfer orbit
In astronautics, the Hohmann transfer orbit () is an orbital maneuver used to transfer a spacecraft between two orbits of different altitudes around a central body. Examples would be used for travel between low Earth orbit and the Moon, or ...
is the simplest maneuver which can be used to move a spacecraft from one altitude to another. Two burns are required: the first to send the craft into the elliptical transfer orbit, and a second to circularize the target orbit.
To raise a circular orbit at , the first posigrade burn raises velocity to the transfer orbit's periapsis velocity:
:
The second posigrade burn, made at apoapsis, raises velocity to the target orbit's velocity:
:
A maneuver to lower the orbit is the mirror image of the raise maneuver; both burns are made retrograde.
=Altitude change by bi-elliptic transfer
=bi-elliptic transfer
In astronautics and aerospace engineering, the bi-elliptic transfer is an orbital maneuver that moves a spacecraft from one orbit to another and may, in certain situations, require less delta-v than a Hohmann transfer maneuver.
The bi-elliptic ...
, which consists of two half-elliptic orbits; the first, posigrade burn sends the spacecraft into an arbitrarily high apoapsis chosen at some point away from the central body. At this point a second burn modifies the periapsis to match the radius of the final desired orbit, where a third, retrograde burn is performed to inject the spacecraft into the desired orbit. While this takes a longer transfer time, a bi-elliptic transfer can require less total propellant than the Hohmann transfer when the ratio of initial and target orbit radii is 12 or greater.
Burn 1 (posigrade):
:
Burn 2 (posigrade or retrograde), to match periapsis to the target orbit's altitude:
:
Burn 3 (retrograde):
:
Change of plane
Plane change maneuvers can be performed alone or in conjunction with other orbit adjustments. For a pure rotation plane change maneuver, consisting only of a change in the inclination of the orbit, the specific angular momentum, ''h'', of the initial and final orbits are equal in magnitude but not in direction. Therefore, the change in specific angular momentum can be written as: : where ''h'' is the specific angular momentum before the plane change, and Δ''i'' is the desired change in the inclination angle. From this it can be shown that the required delta-''v'' is: : From the definition of ''h'', this can also be written as: : where ''v'' is the magnitude of velocity before plane change and ''φ'' is the flight path angle. Using thesmall-angle approximation
The small-angle approximations can be used to approximate the values of the main trigonometric functions, provided that the angle in question is small and is measured in radians:
:
\begin
\sin \theta &\approx \theta \\
\cos \theta &\approx 1 - \ ...
, this becomes:
:
The total delta-''v'' for a combined maneuver can be calculated by a vector addition of the pure rotation delta-''v'' and the delta-''v'' for the other planned orbital change.
Translunar flight
parking orbit
A parking orbit is a temporary orbit used during the launch of a spacecraft. A launch vehicle boosts into the parking orbit, then coasts for a while, then fires again to enter the final desired trajectory. The alternative to a parking orbit is ''di ...
; this allows the flexibility of a bigger launch window
In the context of spaceflight, launch period is the collection of days and launch window is the time period on a given day during which a particular rocket must be launched in order to reach its intended target. If the rocket is not launched wit ...
and more time for checking that the vehicle is in proper condition for the flight.
Escape velocity is not required for flight to the Moon; rather the vehicle's apogee is raised high enough to take it through a point where it enters the Moon's gravitational sphere of influence
In the field of international relations, a sphere of influence (SOI) is a spatial region or concept division over which a state or organization has a level of cultural, economic, military or political exclusivity.
While there may be a formal al ...
(SOI). This is defined as the distance from a satellite at which its gravitational pull on a spacecraft equals that of its central body, which is
:
where ''D'' is the mean distance from the satellite to the central body, and
''m''''c'' and ''m''''s'' are the masses of the central body and satellite, respectively. This value is approximately from Earth's Moon.
An accurate solution of the trajectory requires treatment as a three-body problem
In physics and classical mechanics, the three-body problem is the problem of taking the initial positions and velocities (or momenta) of three point masses and solving for their subsequent motion according to Newton's laws of motion and Newton's ...
, but a preliminary estimate may be made using a patched conic approximation In astrodynamics, the patched conic approximation or patched two-body approximation is a method to simplify trajectory calculations for spacecraft in a multiple-body environment.
Method
The simplification is achieved by dividing space into vario ...
of orbits around the Earth and Moon, patched at the SOI point and taking into account the fact that the Moon is a revolving frame of reference around the Earth.
Translunar injection
This must be timed so that the Moon will be in position to capture the vehicle, and might be modeled to a first approximation as a Hohmann transfer. However, the rocket burn duration is usually long enough, and occurs during a sufficient change in flight path angle, that this is not very accurate. It must be modeled as a non-impulsive maneuver, requiringintegration
Integration may refer to:
Biology
* Multisensory integration
* Path integration
* Pre-integration complex, viral genetic material used to insert a viral genome into a host genome
*DNA integration, by means of site-specific recombinase technolo ...
by finite element analysis
The finite element method (FEM) is a popular method for numerically solving differential equations arising in engineering and mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat t ...
of the accelerations due to propulsive thrust and gravity to obtain velocity and flight path angle:
:
:
:
:
where:
:''F'' is the engine thrust;
:''α'' is the angle of attack;
:''m'' is the vehicle's mass;
:''r'' is the radial distance to the planet's center; and
:''g'' is the gravitational acceleration
In physics, gravitational acceleration is the acceleration of an object in free fall within a vacuum (and thus without experiencing drag (physics), drag). This is the steady gain in speed caused exclusively by the force of gravitational attract ...
, which varies with the inverse square of the radial distance:
::
Altitude , downrange distance , and radial distance from the center of the Earth are then computed as:
:
:
:
Mid-course corrections
A simple lunar trajectory stays in one plane, resulting in lunar flyby or orbit within a small range of inclination to the Moon's equator. This also permits a "free return", in which the spacecraft would return to the appropriate position for reentry into the Earth's atmosphere if it were not injected into lunar orbit. Relatively small velocity changes are usually required to correct for trajectory errors. Such a trajectory was used for theApollo 8
Apollo 8 (December 21–27, 1968) was the first crewed spacecraft to leave low Earth orbit and the first human spaceflight to reach the Moon. The crew orbited the Moon ten times without landing, and then departed safely back to Earth. The ...
, Apollo 10
Apollo 10 (May 18–26, 1969) was a human spaceflight, the fourth crewed mission in the United States Apollo program, and the second (after Apollo8) to orbit the Moon. NASA described it as a "dress rehearsal" for the first Moon landing, an ...
, Apollo 11
Apollo 11 (July 16–24, 1969) was the American spaceflight that first landed humans on the Moon. Commander Neil Armstrong and lunar module pilot Buzz Aldrin landed the Apollo Lunar Module ''Eagle'' on July 20, 1969, at 20:17 UTC, a ...
, and Apollo 12
Apollo 12 (November 14–24, 1969) was the sixth crewed flight in the United States Apollo program and the second to land on the Moon. It was launched on November 14, 1969, by NASA from the Kennedy Space Center, Florida. Commander Charle ...
manned lunar missions.
Greater flexibility in lunar orbital or landing site coverage (at greater angles of lunar inclination) can be obtained by performing a plane change maneuver mid-flight; however, this takes away the free-return option, as the new plane would take the spacecraft's emergency return trajectory away from the Earth's atmospheric re-entry point, and leave the spacecraft in a high Earth orbit. This type of trajectory was used for the last five Apollo missions (13 through 17).
Lunar orbit insertion
In the Apollo program, the retrograde lunar orbit insertion burn was performed at an altitude of approximately on the far side of the Moon. This became the pericynthion of the initial orbits, with an apocynthion on the order of . The delta v was approximately . Two orbits later, the orbit was circularized at . For each mission, the flight dynamics officer prepared 10 lunar orbit insertion solutions so the one could be chosen with the optimum (minimum) fuel burn and best met the mission requirements; this was uploaded to the spacecraft computer and had to be executed and monitored by the astronauts on the lunar far side, while they were out of radio contact with Earth.Interplanetary flight
In order to completely leave one planet's gravitational field to reach another, ahyperbolic
Hyperbolic is an adjective describing something that resembles or pertains to a hyperbola (a curve), to hyperbole (an overstatement or exaggeration), or to hyperbolic geometry.
The following phenomena are described as ''hyperbolic'' because they ...
trajectory relative to the departure planet is necessary, with excess velocity added to (or subtracted from) the departure planet's orbital velocity around the Sun. The desired heliocentric transfer orbit to a superior planet
In the Solar System, a planet is said to be inferior or interior with respect to another planet if its orbit lies inside the other planet's orbit around the Sun. In this situation, the latter planet is said to be superior to the former. In the re ...
will have its perihelion
An apsis (; ) is the farthest or nearest point in the orbit of a planetary body about its primary body. For example, the apsides of the Earth are called the aphelion and perihelion.
General description
There are two apsides in any e ...
at the departure planet, requiring the hyperbolic excess velocity to be applied in the posigrade direction, when the spacecraft is away from the Sun. To an inferior planet
In the Solar System, a planet is said to be inferior or interior with respect to another planet if its orbit lies inside the other planet's orbit around the Sun. In this situation, the latter planet is said to be superior to the former. In the ref ...
destination, aphelion
An apsis (; ) is the farthest or nearest point in the orbit of a planetary body about its primary body. For example, the apsides of the Earth are called the aphelion and perihelion.
General description
There are two apsides in any e ...
will be at the departure planet, and the excess velocity is applied in the retrograde direction when the spacecraft is toward the Sun. For accurate mission calculations, the orbital elements of the planets must be obtained from an ephemeris
In astronomy and celestial navigation, an ephemeris (pl. ephemerides; ) is a book with tables that gives the trajectory of naturally occurring astronomical objects as well as artificial satellites in the sky, i.e., the position (and possibly ...
, such as that published by NASA's Jet Propulsion Laboratory.
Simplifying assumptions
For the purpose of preliminary mission analysis and feasibility studies, certain simplified assumptions may be made to enable delta-v calculation with very small error: *All the planets' orbits exceptMercury
Mercury commonly refers to:
* Mercury (planet), the nearest planet to the Sun
* Mercury (element), a metallic chemical element with the symbol Hg
* Mercury (mythology), a Roman god
Mercury or The Mercury may also refer to:
Companies
* Mercur ...
have very small eccentricity, and therefore may be assumed to be circular at a constant orbital speed and mean distance from the Sun.
*All the planets' orbits (except Mercury) are nearly coplanar, with very small inclination to the ecliptic
The ecliptic or ecliptic plane is the orbital plane of the Earth around the Sun. From the perspective of an observer on Earth, the Sun's movement around the celestial sphere over the course of a year traces out a path along the ecliptic agai ...
(3.39 degrees or less; Mercury's inclination is 7.00 degrees).
*The perturbating effects of the other planets' gravity is negligible.
*The spacecraft will spend most of its flight time under only the gravitational influence of the Sun, except for brief periods when it is in the sphere of influence
In the field of international relations, a sphere of influence (SOI) is a spatial region or concept division over which a state or organization has a level of cultural, economic, military or political exclusivity.
While there may be a formal al ...
of the departure and destination planets.
Since interplanetary spacecraft spend a large period of time in heliocentric orbit
A heliocentric orbit (also called circumsolar orbit) is an orbit around the barycenter of the Solar System, which is usually located within or very near the surface of the Sun. All planets, comets, and asteroids in the Solar System, and the Sun ...
between the planets, which are at relatively large distances away from each other, the patched-conic approximation is much more accurate for interplanetary trajectories than for translunar trajectories. The patch point between the hyperbolic trajectory relative to the departure planet and the heliocentric transfer orbit occurs at the planet's sphere of influence radius relative to the Sun, as defined above in Orbital flight
An orbital spaceflight (or orbital flight) is a spaceflight in which a spacecraft is placed on a trajectory where it could remain in space for at least one orbit. To do this around the Earth, it must be on a free trajectory which has an altit ...
. Given the Sun's mass ratio of 333,432 times that of Earth and distance of , the Earth's sphere of influence radius is (roughly 1,000,000 kilometers).
Heliocentric transfer orbit
The transfer orbit required to carry the spacecraft from the departure planet's orbit to the destination planet is chosen among several options: * AHohmann transfer orbit
In astronautics, the Hohmann transfer orbit () is an orbital maneuver used to transfer a spacecraft between two orbits of different altitudes around a central body. Examples would be used for travel between low Earth orbit and the Moon, or ...
requires the least possible propellant and delta-v; this is half of an elliptical orbit with aphelion and perihelion tangential to both planets' orbits, with the longest outbound flight time equal to half the period of the ellipse. This is known as a conjunction
Conjunction may refer to:
* Conjunction (grammar), a part of speech
* Logical conjunction, a mathematical operator
** Conjunction introduction, a rule of inference of propositional logic
* Conjunction (astronomy), in which two astronomical bodies ...
-class mission. There is no "free return" option, because if the spacecraft does not enter orbit around the destination planet and instead completes the transfer orbit, the departure planet will not be in its original position. Using another Hohmann transfer to return requires a significant loiter time at the destination planet, resulting in a very long total round-trip mission time. Science fiction writer Arthur C. Clarke
Sir Arthur Charles Clarke (16 December 191719 March 2008) was an English science-fiction writer, science writer, futurist, inventor, undersea explorer, and television series host.
He co-wrote the screenplay for the 1968 film '' 2001: A Spac ...
wrote in his 1951 book ''The Exploration of Space'' that an Earth-to-Mars round trip would require 259 days outbound and another 259 days inbound, with a 425-day stay at Mars.
* Increasing the departure apsis speed (and thus the semi-major axis) results in a trajectory which crosses the destination planet's orbit non-tangentially before reaching the opposite apsis, increasing delta-v but cutting the outbound transit time below the maximum.
* A gravity assist
In orbital mechanics and aerospace engineering, a gravitational slingshot, gravity assist maneuver, or swing-by is the use of the relative movement (e.g. orbit around the Sun) and gravity of a planet or other astronomical object to alter the ...
maneuver, sometimes known as a "slingshot maneuver" or ''Crocco mission'' after its 1956 proposer Gaetano Crocco
Gaetano Arturo Crocco (26 October 1877 – 19 January 1968) was an Italian scientist and aeronautics pioneer, the founder of the Italian Rocket Society, and went on to become Italy's leading space scientist. He was born in Naples.
In 1927, Croc ...
, results in an opposition
Opposition may refer to:
Arts and media
* ''Opposition'' (Altars EP), 2011 EP by Christian metalcore band Altars
* The Opposition (band), a London post-punk band
* '' The Opposition with Jordan Klepper'', a late-night television series on Com ...
-class mission with a much shorter dwell time at the destination. This is accomplished by swinging past another planet, using its gravity to alter the orbit. A round trip to Mars, for example, can be significantly shortened from the 943 days required for the conjunction mission, to under a year, by swinging past Venus on return to the Earth.
Hyperbolic departure
The required hyperbolic excess velocity ''v''∞ (sometimes called ''characteristic velocity'') is the difference between the transfer orbit's departure speed and the departure planet's heliocentric orbital speed. Once this is determined, the injection velocity relative to the departure planet at periapsis is: : The excess velocity vector for a hyperbola is displaced from the periapsis tangent by a characteristic angle, therefore the periapsis injection burn must lead the planetary departure point by the same angle: : The geometric equation for eccentricity of an ellipse cannot be used for a hyperbola. But the eccentricity can be calculated from dynamics formulations as: : where h is the specific angular momentum as given above in theOrbital flight
An orbital spaceflight (or orbital flight) is a spaceflight in which a spacecraft is placed on a trajectory where it could remain in space for at least one orbit. To do this around the Earth, it must be on a free trajectory which has an altit ...
section, calculated at the periapsis:
:
and ''ε'' is the specific energy:
:
Also, the equations for r and v given in Orbital flight
An orbital spaceflight (or orbital flight) is a spaceflight in which a spacecraft is placed on a trajectory where it could remain in space for at least one orbit. To do this around the Earth, it must be on a free trajectory which has an altit ...
depend on the semi-major axis, and thus are unusable for an escape trajectory. But setting radius at periapsis equal to the r equation at zero
anomaly gives an alternate expression for the semi-latus rectum:
:
which gives a more general equation for radius versus anomaly which is usable at any eccentricity:
:
Substituting the alternate expression for p also gives an alternate expression for a (which is defined for a hyperbola, but no longer represents the semi-major axis). This gives an equation for velocity versus radius which is likewise usable at any eccentricity:
:
The equations for flight path angle and anomaly versus time given in Orbital flight
An orbital spaceflight (or orbital flight) is a spaceflight in which a spacecraft is placed on a trajectory where it could remain in space for at least one orbit. To do this around the Earth, it must be on a free trajectory which has an altit ...
are also usable for hyperbolic trajectories.
Launch windows
There is a great deal of variation with time of the velocity change required for a mission, because of the constantly varying relative positions of the planets. Therefore, optimum launch windows are often chosen from the results ofporkchop plot
In orbital mechanics, a porkchop plot (also pork-chop plot) is a chart that shows contours of equal characteristic energy (C3) against combinations of launch date and arrival date for a particular interplanetary flight.
By examining the result ...
s that show contours of characteristic energy (v∞2) plotted versus departure and arrival time.
Atmospheric entry
Controlled entry, descent, and landing of a vehicle is achieved by shedding the excess kinetic energy throughaerodynamic heating
Aerodynamic heating is the heating of a solid body produced by its high-speed passage through air. In science and engineering, an understanding of aerodynamic heating is necessary for predicting the behaviour of meteoroids which enter the earth's ...
from drag, which requires some means of heat shielding, and/or retrograde thrust. Terminal descent is usually achieved by means of parachutes and/or air brakes.
Attitude control
Since spacecraft spend most of their flight time coasting unpowered through thevacuum
A vacuum is a space devoid of matter. The word is derived from the Latin adjective ''vacuus'' for "vacant" or " void". An approximation to such vacuum is a region with a gaseous pressure much less than atmospheric pressure. Physicists often di ...
of space, they are unlike aircraft in that their flight trajectory is not determined by their attitude (orientation), except during atmospheric flight to control the forces of lift and drag, and during powered flight to align the thrust vector. Nonetheless, attitude control is often maintained in unpowered flight to keep the spacecraft in a fixed orientation for purposes of astronomical observation
Observational astronomy is a division of astronomy that is concerned with recording data about the observable universe, in contrast with theoretical astronomy, which is mainly concerned with calculating the measurable implications of physical ...
, communications, or for solar power
Solar power is the conversion of energy from sunlight into electricity, either directly using photovoltaics (PV) or indirectly using concentrated solar power. Photovoltaic cells convert light into an electric current using the photovoltaic ef ...
generation; or to place it into a controlled spin for passive thermal control
A thermal column (or thermal) is a rising mass of buoyant air, a convective current in the atmosphere, that transfers heat energy vertically. Thermals are created by the uneven heating of Earth's surface from solar radiation, and are an example ...
, or to create artificial gravity inside the craft.
Attitude control is maintained with respect to an inertial frame of reference or another entity (the celestial sphere, certain fields, nearby objects, etc.). The attitude of a craft is described by angles relative to three mutually perpendicular axes of rotation, referred to as roll, pitch, and yaw. Orientation can be determined by calibration using an external guidance system, such as determining the angles to a reference star or the Sun, then internally monitored using an inertial system of mechanical or optical gyroscopes
A gyroscope (from Ancient Greek γῦρος ''gŷros'', "round" and σκοπέω ''skopéō'', "to look") is a device used for measuring or maintaining orientation and angular velocity. It is a spinning wheel or disc in which the axis of rotat ...
. Orientation is a vector quantity described by three angles for the instantaneous direction, and the instantaneous rates of roll in all three axes of rotation. The aspect of control implies both awareness of the instantaneous orientation and rates of roll and the ability to change the roll rates to assume a new orientation using either a reaction control system
A reaction control system (RCS) is a spacecraft system that uses thrusters to provide attitude control and translation. Alternatively, reaction wheels are used for attitude control. Use of diverted engine thrust to provide stable attitude con ...
or other means.
Newton's second law, applied to rotational rather than linear motion, becomes:
:
where is the net torque
In physics and mechanics, torque is the rotational equivalent of linear force. It is also referred to as the moment of force (also abbreviated to moment). It represents the capability of a force to produce change in the rotational motion of t ...
about an axis of rotation exerted on the vehicle, Ix is its moment of inertia
The moment of inertia, otherwise known as the mass moment of inertia, angular mass, second moment of mass, or most accurately, rotational inertia, of a rigid body is a quantity that determines the torque needed for a desired angular accele ...
about that axis (a physical property that combines the mass and its distribution around the axis), and is the angular acceleration
In physics, angular acceleration refers to the time rate of change of angular velocity. As there are two types of angular velocity, namely spin angular velocity and orbital angular velocity, there are naturally also two types of angular acceler ...
about that axis in radians per second per second. Therefore, the acceleration rate in degrees per second per second is
:
Analogous to linear motion, the angular rotation rate (degrees per second) is obtained by integrating α over time:
:
and the angular rotation is the time integral of the rate:
:
The three principal moments of inertia Ix, Iy, and Iz about the roll, pitch and yaw axes, are determined through the vehicle's center of mass.
The control torque for a launch vehicle is sometimes provided aerodynamically by movable fins, and usually by mounting the engines on gimbals to vector the thrust around the center of mass. Torque is frequently applied to spacecraft, operating absent aerodynamic forces, by a reaction control system
A reaction control system (RCS) is a spacecraft system that uses thrusters to provide attitude control and translation. Alternatively, reaction wheels are used for attitude control. Use of diverted engine thrust to provide stable attitude con ...
, a set of thrusters located about the vehicle. The thrusters are fired, either manually or under automatic guidance control, in short bursts to achieve the desired rate of rotation, and then fired in the opposite direction to halt rotation at the desired position. The torque about a specific axis is:
:
where r is its distance from the center of mass, and F is the thrust of an individual thruster (only the component of F perpendicular to r is included.)
For situations where propellant consumption may be a problem (such as long-duration satellites or space stations), alternative means may be used to provide the control torque, such as reaction wheel
A reaction wheel (RW) is used primarily by spacecraft for three-axis attitude control, and does not require rockets or external applicators of torque. They provide a high pointing accuracy, and are particularly useful when the spacecraft must be ...
s or control moment gyroscope
A control moment gyroscope (CMG) is an attitude control device generally used in spacecraft attitude control systems. A CMG consists of a spinning rotor and one or more motorized gimbals that tilt the rotor’s angular momentum. As the rotor tilt ...
s.
Notes
References
* * * * * * * * * * * *Sidi, M.J. "Spacecraft Dynamics & Control. Cambridge, 1997. *Thomson, W.T. "Introduction to Space Dynamics." Dover, 1961. *Wertz, J.R. "Spacecraft Attitude Determination and Control." Kluwer, 1978. *Wiesel, W.E. "Spaceflight Dynamics." McGraw-Hill, 1997. {{DEFAULTSORT:Flight Dynamics (Satellites) Astrodynamics Spaceflight concepts