Equation of time on:
[Wikipedia]
[Google]
[Amazon]
 The equation of time describes the discrepancy between two kinds of
The equation of time describes the discrepancy between two kinds of
 The United States Naval Observatory states "the Equation of Time is the difference ''apparent solar time'' minus ''mean solar time''", i.e. if the sun is ahead of the clock the sign is positive, and if the clock is ahead of the sun the sign is negative. The equation of time is shown in the upper graph above for a period of slightly more than a year. The lower graph (which covers exactly one calendar year) has the same absolute values but the
The United States Naval Observatory states "the Equation of Time is the difference ''apparent solar time'' minus ''mean solar time''", i.e. if the sun is ahead of the clock the sign is positive, and if the clock is ahead of the sun the sign is negative. The equation of time is shown in the upper graph above for a period of slightly more than a year. The lower graph (which covers exactly one calendar year) has the same absolute values but the
 From 1767 to 1833, the British '' Nautical Almanac and Astronomical Ephemeris'' tabulated the equation of time in the sense 'add or subtract (as directed) the number of minutes and seconds stated to or from the apparent time to obtain the mean time'. Times in the Almanac were in apparent solar time, because time aboard ship was most often determined by observing the Sun. This operation would be performed in the unusual case that the mean solar time of an observation was needed. In the issues since 1834, all times have been in mean solar time, because by then the time aboard ship was increasingly often determined by
From 1767 to 1833, the British '' Nautical Almanac and Astronomical Ephemeris'' tabulated the equation of time in the sense 'add or subtract (as directed) the number of minutes and seconds stated to or from the apparent time to obtain the mean time'. Times in the Almanac were in apparent solar time, because time aboard ship was most often determined by observing the Sun. This operation would be performed in the unusual case that the mean solar time of an observation was needed. In the issues since 1834, all times have been in mean solar time, because by then the time aboard ship was increasingly often determined by
 The Earth revolves around the Sun. As seen from Earth, the Sun appears to revolve once around the Earth through the background stars in one year. If the Earth orbited the Sun with a constant speed, in a circular orbit in a plane perpendicular to the Earth's axis, then the Sun would culminate every day at exactly the same time, and be a perfect time keeper (except for the very small effect of the slowing rotation of the Earth). But the orbit of the Earth is an ellipse not centered on the Sun, and its speed varies between 30.287 and 29.291 km/s, according to
The Earth revolves around the Sun. As seen from Earth, the Sun appears to revolve once around the Earth through the background stars in one year. If the Earth orbited the Sun with a constant speed, in a circular orbit in a plane perpendicular to the Earth's axis, then the Sun would culminate every day at exactly the same time, and be a perfect time keeper (except for the very small effect of the slowing rotation of the Earth). But the orbit of the Earth is an ellipse not centered on the Sun, and its speed varies between 30.287 and 29.291 km/s, according to
where: * GAST is the Greenwich apparent
 All these angles are shown in the figure on the right, which shows the
All these angles are shown in the figure on the right, which shows the
 Here is the value of at the chosen date and time. For the values given here, in radians, is that measured for the actual Sun at the epoch, 1 January 2000 at 12 noon UT1, and is the number of days past that epoch. At periapsis , so solving gives = . This puts the periapsis on 4 January 2000 at 00:11:41 while the actual periapsis is, according to results from the ''Multiyear Interactive Computer Almanac'' (abbreviated as MICA), on 3 January 2000 at 05:17:30. This large discrepancy happens because the difference between the orbital radius at the two locations is only 1 part in a million; in other words, radius is a very weak function of time near periapsis. As a practical matter this means that one cannot get a highly accurate result for the equation of time by using and adding the actual periapsis date for a given year. However, high accuracy can be achieved by using the formulation in terms of .
When , ''M'' is greater than 2 and one must subtract a multiple of 2 (that depends on the year) from it to bring it into the range 0 to 2. Likewise for years prior to 2000 one must add multiples of 2. For example, for the year 2010, varies from on 1 January at noon to on 31 December at noon; the corresponding values are and and are reduced to the range 0 to 2 by subtracting 10 and 11 times 2 respectively.
One can always write:
5)
where:
* = number of days from the epoch to noon on 1 January of the desired year
* (365 if the calculation is for a leap year).
The resulting equation for years after 2000, written as a sum of two terms, given 1), 4) and 5), is:
6) inutes
In plain text format:
7) EoT = -7.659sin(6.24004077 + 0.01720197(365*(y-2000) + d)) + 9.863sin( 2 (6.24004077 + 0.01720197 (365*(y-2000) + d)) + 3.5932 ) inutes
Term "a" represents the contribution of eccentricity, term "b" represents contribution of obliquity.
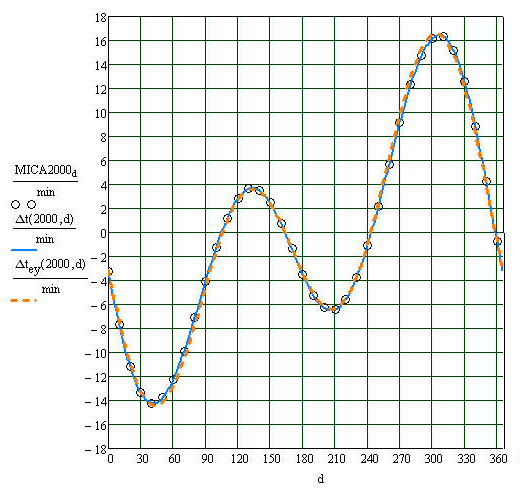
The result of the computations is usually given as either a set of tabular values, or a graph of the equation of time as a function of . A comparison of plots of , , and results from MICA all for the year 2000 is shown in the figure. The plot of is seen to be close to the results produced by MICA, the absolute error, , is less than 1 minute throughout the year; its largest value is 43.2 seconds and occurs on day 276 (3 October). The plot of is indistinguishable from the results of MICA, the largest absolute error between the two is 2.46 s on day 324 (20 November).
Here is the value of at the chosen date and time. For the values given here, in radians, is that measured for the actual Sun at the epoch, 1 January 2000 at 12 noon UT1, and is the number of days past that epoch. At periapsis , so solving gives = . This puts the periapsis on 4 January 2000 at 00:11:41 while the actual periapsis is, according to results from the ''Multiyear Interactive Computer Almanac'' (abbreviated as MICA), on 3 January 2000 at 05:17:30. This large discrepancy happens because the difference between the orbital radius at the two locations is only 1 part in a million; in other words, radius is a very weak function of time near periapsis. As a practical matter this means that one cannot get a highly accurate result for the equation of time by using and adding the actual periapsis date for a given year. However, high accuracy can be achieved by using the formulation in terms of .
When , ''M'' is greater than 2 and one must subtract a multiple of 2 (that depends on the year) from it to bring it into the range 0 to 2. Likewise for years prior to 2000 one must add multiples of 2. For example, for the year 2010, varies from on 1 January at noon to on 31 December at noon; the corresponding values are and and are reduced to the range 0 to 2 by subtracting 10 and 11 times 2 respectively.
One can always write:
5)
where:
* = number of days from the epoch to noon on 1 January of the desired year
* (365 if the calculation is for a leap year).
The resulting equation for years after 2000, written as a sum of two terms, given 1), 4) and 5), is:
6) inutes
In plain text format:
7) EoT = -7.659sin(6.24004077 + 0.01720197(365*(y-2000) + d)) + 9.863sin( 2 (6.24004077 + 0.01720197 (365*(y-2000) + d)) + 3.5932 ) inutes
Term "a" represents the contribution of eccentricity, term "b" represents contribution of obliquity.
The result of the computations is usually given as either a set of tabular values, or a graph of the equation of time as a function of . A comparison of plots of , , and results from MICA all for the year 2000 is shown in the figure. The plot of is seen to be close to the results produced by MICA, the absolute error, , is less than 1 minute throughout the year; its largest value is 43.2 seconds and occurs on day 276 (3 October). The plot of is indistinguishable from the results of MICA, the largest absolute error between the two is 2.46 s on day 324 (20 November).
NOAA Solar Calculator
* (include rise/set/transit times of the Sun and other celestial objects)
The equation of time
described on the
The Equation of Time and the Analemma
by Kieron Taylor
containing a link to a C program using a more accurate formula than most (particularly at high inclinations and eccentricities). The program can calculate solar declination, Equation of Time, or Analemma
* ttps://web.archive.org/web/20140318064248/http://www.pendulumofmayfair.co.uk/view.asp?pid=272&cat=Longcase%20Clocks Equation of Time Longcase Clock by John Topping C.1720
The equation of time correction-table
A page describing how to correct a clock to a sundial
Calculate your solar time, including the equation of time {{DEFAULTSORT:Equation of Time Dynamics of the Solar System Timekeeping Time in astronomy Earth phenomena Sundials Equations
solar time
Solar time is a calculation of the passage of time based on the position of the Sun in the sky. The fundamental unit of solar time is the day, based on the synodic rotation period. Traditionally, there are three types of time reckoning based ...
. The two times that differ are the apparent solar time, which directly tracks the diurnal motion of the Sun
The Sun is the star at the centre of the Solar System. It is a massive, nearly perfect sphere of hot plasma, heated to incandescence by nuclear fusion reactions in its core, radiating the energy from its surface mainly as visible light a ...
, and mean solar time
Solar time is a calculation of the passage of time based on the position of the Sun in the sky. The fundamental unit of solar time is the day, based on the synodic rotation period. Traditionally, there are three types of time reckoning based ...
, which tracks a theoretical mean
A mean is a quantity representing the "center" of a collection of numbers and is intermediate to the extreme values of the set of numbers. There are several kinds of means (or "measures of central tendency") in mathematics, especially in statist ...
Sun with uniform motion along the celestial equator
The celestial equator is the great circle of the imaginary celestial sphere on the same plane as the equator of Earth. By extension, it is also a plane of reference in the equatorial coordinate system. Due to Earth's axial tilt, the celestial ...
. Apparent solar time can be obtained by measurement of the current position (hour angle
In astronomy and celestial navigation, the hour angle is the dihedral angle between the '' meridian plane'' (containing Earth's axis and the zenith) and the '' hour circle'' (containing Earth's axis and a given point of interest).
It may be ...
) of the Sun, as indicated (with limited accuracy) by a sundial
A sundial is a horology, horological device that tells the time of day (referred to as civil time in modern usage) when direct sunlight shines by the position of the Sun, apparent position of the Sun in the sky. In the narrowest sense of the ...
. ''Mean'' solar time, for the same place, would be the time indicated by a steady clock set so that over the year its differences from apparent solar time would have a mean of zero.
The equation of time is the east or west component of the analemma
In astronomy, an analemma (; ) is a diagram showing the position of the Sun in the sky as seen from a fixed location on Earth at the same Solar time#Mean solar time, mean solar time over the course of a year. The change of position is a result ...
, a curve representing the angular offset of the Sun from its mean position on the celestial sphere
In astronomy and navigation, the celestial sphere is an abstract sphere that has an arbitrarily large radius and is concentric to Earth. All objects in the sky can be conceived as being projected upon the inner surface of the celestial sphere, ...
as viewed from Earth. The equation of time values for each day of the year, compiled by astronomical observatories
An observatory is a location used for observing terrestrial, marine, or celestial events. Astronomy, climatology/meteorology, geophysics, oceanography and volcanology are examples of disciplines for which observatories have been constructed.
Th ...
, were widely listed in almanac
An almanac (also spelled almanack and almanach) is a regularly published listing of a set of current information about one or multiple subjects. It includes information like weather forecasting, weather forecasts, farmers' sowing, planting dates ...
s and ephemerides.
The equation of time can be approximated by a sum of two sine wave
A sine wave, sinusoidal wave, or sinusoid (symbol: ∿) is a periodic function, periodic wave whose waveform (shape) is the trigonometric function, trigonometric sine, sine function. In mechanics, as a linear motion over time, this is ''simple ...
s:
: inutes
where:
where represents the number of days since 1 January of the current year, .
Concept
During a year the equation of time varies as shown on the graph; its change from one year to the next is slight. Apparent time, and the sundial, can be ahead (fast) by as much as 16 min 33 s (around 3 November), or behind (slow) by as much as 14 min 6 s (around 11 February). The equation of time has zeros near 15 April, 13 June, 1 September, and 25 December. Ignoring very slow changes in the Earth's orbit and rotation, these events are repeated at the same times everytropical year
A tropical year or solar year (or tropical period) is the time that the Sun takes to return to the same position in the sky – as viewed from the Earth or another celestial body of the Solar System – thus completing a full cycle of astronom ...
. However, due to the non-integral number of days in a year, these dates can vary by a day or so from year to year. As an example of the inexactness of the dates, according to the U.S. Naval Observatory's ''Multiyear Interactive Computer Almanac'' the equation of time was zero at 02:00 UT1 on 16 April 2011.
The graph of the equation of time is closely approximated by the sum of two sine curves, one with a period of a year and one with a period of half a year. The curves reflect two astronomical effects, each causing a different non-uniformity in the apparent daily motion of the Sun relative to the stars:
* the obliquity of the ecliptic
The ecliptic or ecliptic plane is the orbital plane of Earth's orbit, Earth around the Sun. It was a central concept in a number of ancient sciences, providing the framework for key measurements in astronomy, astrology and calendar-making.
Fr ...
(the plane of the Earth's annual orbital motion around the Sun), which is inclined by about 23.44 degrees relative to the plane of the Earth's equator
The equator is the circle of latitude that divides Earth into the Northern Hemisphere, Northern and Southern Hemisphere, Southern Hemispheres of Earth, hemispheres. It is an imaginary line located at 0 degrees latitude, about in circumferen ...
; and
* the eccentricity
Eccentricity or eccentric may refer to:
* Eccentricity (behavior), odd behavior on the part of a person, as opposed to being "normal"
Mathematics, science and technology Mathematics
* Off-Centre (geometry), center, in geometry
* Eccentricity (g ...
of the Earth's orbit
Earth orbits the Sun at an astronomical unit, average distance of , or 8.317 light-second, light-minutes, in a retrograde and prograde motion, counterclockwise direction as viewed from above the Northern Hemisphere. One complete orbit takes & ...
around the Sun, which is about 0.0167.
The equation of time vanishes only for a planet with zero axial tilt and zero orbital eccentricity. Two examples of planets with large equations of time are Mars and Uranus. On Mars
Mars is the fourth planet from the Sun. It is also known as the "Red Planet", because of its orange-red appearance. Mars is a desert-like rocky planet with a tenuous carbon dioxide () atmosphere. At the average surface level the atmosph ...
the difference between sundial time and clock time can be as much as 50 minutes, due to the considerably greater eccentricity of its orbit. The planet Uranus
Uranus is the seventh planet from the Sun. It is a gaseous cyan-coloured ice giant. Most of the planet is made of water, ammonia, and methane in a Supercritical fluid, supercritical phase of matter, which astronomy calls "ice" or Volatile ( ...
, which has an extremely large axial tilt, has an equation of time that makes its days start and finish several hours earlier or later depending on where it is in its orbit.
Notation
 The United States Naval Observatory states "the Equation of Time is the difference ''apparent solar time'' minus ''mean solar time''", i.e. if the sun is ahead of the clock the sign is positive, and if the clock is ahead of the sun the sign is negative. The equation of time is shown in the upper graph above for a period of slightly more than a year. The lower graph (which covers exactly one calendar year) has the same absolute values but the
The United States Naval Observatory states "the Equation of Time is the difference ''apparent solar time'' minus ''mean solar time''", i.e. if the sun is ahead of the clock the sign is positive, and if the clock is ahead of the sun the sign is negative. The equation of time is shown in the upper graph above for a period of slightly more than a year. The lower graph (which covers exactly one calendar year) has the same absolute values but the sign
A sign is an object, quality, event, or entity whose presence or occurrence indicates the probable presence or occurrence of something else. A natural sign bears a causal relation to its object—for instance, thunder is a sign of storm, or me ...
is reversed as it shows how far the clock is ahead of the sun. Publications may use either format: in the English-speaking world, the former usage is the more common, but is not always followed. Anyone who makes use of a published table or graph should first check its sign usage. Often, there is a note or caption which explains it. Otherwise, the usage can be determined by knowing that, during the first three months of each year, the clock is ahead of the sundial. The mnemonic
A mnemonic device ( ), memory trick or memory device is any learning technique that aids information retention or retrieval in the human memory, often by associating the information with something that is easier to remember.
It makes use of e ...
"NYSS" (pronounced "nice"), for "new year, sundial slow", can be useful. Some published tables avoid the ambiguity by not using signs, but by showing phrases such as "sundial fast" or "sundial slow" instead.
History
The phrase "equation of time" is derived from themedieval Latin
Medieval Latin was the form of Literary Latin used in Roman Catholic Church, Roman Catholic Western Europe during the Middle Ages. It was also the administrative language in the former Western Roman Empire, Roman Provinces of Mauretania, Numidi ...
''aequātiō diērum'', meaning "equation of days" or "difference of days". The word ''equation'' is used in the medieval sense of "reconciliation of a difference". The word '' aequātiō'' (and Middle English
Middle English (abbreviated to ME) is a form of the English language that was spoken after the Norman Conquest of 1066, until the late 15th century. The English language underwent distinct variations and developments following the Old English pe ...
''equation
In mathematics, an equation is a mathematical formula that expresses the equality of two expressions, by connecting them with the equals sign . The word ''equation'' and its cognates in other languages may have subtly different meanings; for ...
'') was used in medieval astronomy to tabulate the difference between an observed value and the expected value (as in the equation of the centre, the equation of the equinoxes, the equation of the epicycle). Gerald J. Toomer uses the medieval term "equation", from the Latin ''aequātiō'' (equalization or adjustment), for Ptolemy's difference between the mean solar time and the apparent solar time. Johannes Kepler
Johannes Kepler (27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, Natural philosophy, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best know ...
's definition of the equation is "the difference between the number of degrees and minutes of the mean anomaly and the degrees and minutes of the corrected anomaly."
The difference between apparent solar time and mean time was recognized by astronomers since antiquity, but prior to the invention of accurate mechanical clocks in the mid-17th century, sundial
A sundial is a horology, horological device that tells the time of day (referred to as civil time in modern usage) when direct sunlight shines by the position of the Sun, apparent position of the Sun in the sky. In the narrowest sense of the ...
s were the only reliable timepieces, and apparent solar time was the generally accepted standard. Mean time did not supplant apparent time in national almanacs and ephemerides until the early 19th century.
Early astronomy
The irregular daily movement of the Sun was known to the Babylonians. Book III ofPtolemy
Claudius Ptolemy (; , ; ; – 160s/170s AD) was a Greco-Roman mathematician, astronomer, astrologer, geographer, and music theorist who wrote about a dozen scientific treatises, three of which were important to later Byzantine science, Byzant ...
's ''Almagest
The ''Almagest'' ( ) is a 2nd-century Greek mathematics, mathematical and Greek astronomy, astronomical treatise on the apparent motions of the stars and planetary paths, written by Ptolemy, Claudius Ptolemy ( ) in Koine Greek. One of the most i ...
'' (2nd century) is primarily concerned with the Sun's anomaly, and he tabulated the equation of time in his ''Handy Tables''. Ptolemy discusses the correction needed to convert the meridian crossing of the Sun to mean solar time and takes into consideration the nonuniform motion of the Sun along the ecliptic and the meridian correction for the Sun's ecliptic longitude. He states the maximum correction is time-degrees or of an hour (Book III, chapter 9). However he did not consider the effect to be relevant for most calculations since it was negligible for the slow-moving luminaries and only applied it for the fastest-moving luminary, the Moon.
Based on Ptolemy's discussion in the ''Almagest
The ''Almagest'' ( ) is a 2nd-century Greek mathematics, mathematical and Greek astronomy, astronomical treatise on the apparent motions of the stars and planetary paths, written by Ptolemy, Claudius Ptolemy ( ) in Koine Greek. One of the most i ...
'', values for the equation of time (Arabic ''taʿdīl al-ayyām bi layālayhā'') were standard for the tables (''zij'') in the works of medieval Islamic astronomy.
Early modern period
A description of apparent and mean time was given byNevil Maskelyne
Nevil Maskelyne (; 6 October 1732 – 9 February 1811) was the fifth British Astronomer Royal. He held the office from 1765 to 1811. He was the first person to scientifically measure the mass of the planet Earth. He created '' The Nautical Al ...
in the ''Nautical Almanac'' for 1767: "Apparent Time is that deduced immediately from the Sun, whether from the Observation of his passing the Meridian, or from his observed Rising or Setting. This Time is different from that shewn by Clocks and Watches well regulated at Land, which is called equated or mean Time." He went on to say that, at sea, the apparent time found from observation of the Sun must be corrected by the equation of time, if the observer requires the mean time.
The right time was originally considered to be that which was shown by a sundial. When good mechanical clocks were introduced, they agreed with sundials only near four dates each year, so the equation of time was used to "correct" their readings to obtain sundial time. Some clocks, called equation clocks, included an internal mechanism to perform this "correction". Later, as clocks became the dominant good timepieces, uncorrected clock time, i.e., "mean time", became the accepted standard. The readings of sundials, when they were used, were then, and often still are, corrected with the equation of time, used in the reverse direction from previously, to obtain clock time. Many sundials, therefore, have tables or graphs of the equation of time engraved on them to allow the user to make this correction.
The equation of time was used historically to set clocks. Between the invention of accurate clocks in 1656 and the advent of commercial time distribution services around 1900, there were several common land-based ways to set clocks. A sundial was read and corrected with the table or graph of the equation of time.
If a transit instrument
In astronomy, a transit instrument is a small telescope with an extremely precisely graduated mount used for the precise observation of star positions. They were previously widely used in astronomical observatories and naval observatories to m ...
was available or accuracy was important, the sun's transit across the meridian (the moment the sun appears to be due south or north of the observer, known as its culmination
In observational astronomy, culmination is the passage of a celestial object (such as the Sun, the Moon, a planet, a star, constellation or a deep-sky object) across the observer's local meridian. These events are also known as meridian tran ...
) was noted; the clock was then set to noon and offset by the number of minutes given by the equation of time for that date. A third method did not use the equation of time; instead, it used stellar observations to give sidereal time
Sidereal time ("sidereal" pronounced ) is a system of timekeeping used especially by astronomers. Using sidereal time and the celestial coordinate system, it is easy to locate the positions of celestial objects in the night sky. Sidereal t ...
, exploiting the relationship between sidereal time and mean solar time
Solar time is a calculation of the passage of time based on the position of the Sun in the sky. The fundamental unit of solar time is the day, based on the synodic rotation period. Traditionally, there are three types of time reckoning based ...
. The more accurate methods were also precursors to finding the observer's longitude
Longitude (, ) is a geographic coordinate that specifies the east- west position of a point on the surface of the Earth, or another celestial body. It is an angular measurement, usually expressed in degrees and denoted by the Greek lett ...
in relation to a prime meridian
A prime meridian is an arbitrarily chosen meridian (geography), meridian (a line of longitude) in a geographic coordinate system at which longitude is defined to be 0°. On a spheroid, a prime meridian and its anti-meridian (the 180th meridian ...
, such as in geodesy
Geodesy or geodetics is the science of measuring and representing the Figure of the Earth, geometry, Gravity of Earth, gravity, and Earth's rotation, spatial orientation of the Earth in Relative change, temporally varying Three-dimensional spac ...
on land and celestial navigation
Celestial navigation, also known as astronavigation, is the practice of position fixing using stars and other celestial bodies that enables a navigator to accurately determine their actual current physical position in space or on the surface ...
on the sea.
The first tables to give the equation of time in an essentially correct way were published in 1665 by Christiaan Huygens
Christiaan Huygens, Halen, Lord of Zeelhem, ( , ; ; also spelled Huyghens; ; 14 April 1629 – 8 July 1695) was a Dutch mathematician, physicist, engineer, astronomer, and inventor who is regarded as a key figure in the Scientific Revolution ...
. Huygens, following the tradition of Ptolemy and medieval astronomers in general, set his values for the equation of time so as to make all values positive throughout the year. This meant that any clock being set to mean time by Huygens's tables was consistently about 15 minutes slow compared to today's mean time.
Another set of tables was published in 1672–73 by John Flamsteed
John Flamsteed (19 August 1646 – 31 December 1719) was an English astronomer and the first Astronomer Royal. His main achievements were the preparation of a 3,000-star catalogue, ''Catalogus Britannicus'', and a star atlas called '' Atlas ...
, who later became the first Astronomer Royal
Astronomer Royal is a senior post in the Royal Households of the United Kingdom. There are two officers, the senior being the astronomer royal dating from 22 June 1675; the junior is the astronomer royal for Scotland dating from 1834. The Astro ...
of the new Royal Greenwich Observatory
The Royal Observatory, Greenwich (ROG; known as the Old Royal Observatory from 1957 to 1998, when the working Royal Greenwich Observatory, RGO, temporarily moved south from Greenwich to Herstmonceux) is an observatory situated on a hill in G ...
. These appear to have been the first essentially correct tables that gave today's meaning of Mean Time (previously, as noted above, the sign of the equation was always positive and it was set at zero when the apparent time of sunrise was earliest relative to the clock time of sunrise). Flamsteed adopted the convention of tabulating and naming the correction in the sense that it was to be applied to the apparent time to give mean time.
The equation of time, correctly based on the two major components of the Sun's irregularity of apparent motion, was not generally adopted until after Flamsteed's tables of 1672–73, published with the posthumous edition of the works of Jeremiah Horrocks.
Robert Hooke
Robert Hooke (; 18 July 16353 March 1703) was an English polymath who was active as a physicist ("natural philosopher"), astronomer, geologist, meteorologist, and architect. He is credited as one of the first scientists to investigate living ...
(1635–1703), who mathematically analyzed the universal joint
A universal joint (also called a universal coupling or U-joint) is a joint or coupling connecting rigid shafts whose axes are inclined to each other. It is commonly used in shafts that transmit rotary motion. It consists of a pair of hinges ...
, was the first to note that the geometry and mathematical description of the (non-secular) equation of time and the universal joint were identical, and proposed the use of a universal joint in the construction of a "mechanical sundial".
18th and early 19th centuries
The corrections in Flamsteed's tables of 1672–1673 and 1680 gave mean time computed essentially correctly and without need for further offset. But the numerical values in tables of the equation of time have somewhat changed since then, owing to three factors: * General improvements in accuracy that came from refinements in astronomical measurement techniques, * Slow intrinsic changes in the equation of time, occurring as a result of small long-term changes in the Earth's obliquity and eccentricity (affecting, for instance, the distance and dates ofperihelion
An apsis (; ) is the farthest or nearest point in the orbit of a planetary body about its primary body. The line of apsides (also called apse line, or major axis of the orbit) is the line connecting the two extreme values.
Apsides perta ...
), and
* The inclusion of small sources of additional variation in the apparent motion of the Sun, unknown in the 17th century but discovered from the 18th century onwards, including the effects of the Moon (See barycentre), Venus and Jupiter.
marine chronometer
A marine chronometer is a precision timepiece that is carried on a ship and employed in the determination of the ship's position by celestial navigation. It is used to determine longitude by comparing Greenwich Mean Time (GMT), and the time at t ...
s. The instructions were consequently to add or subtract (as directed) the number of minutes stated to or from the mean time to obtain the apparent time. So now addition corresponded to the equation being positive and subtraction corresponded to it being negative.
As the apparent daily movement of the Sun is one revolution per day, that is 360° every 24 hours, and the Sun itself appears as a disc of about 0.5° in the sky, simple sundials can be read to a maximum accuracy of about one minute. Since the equation of time has a range of about 33 minutes, the difference between sundial time and clock time cannot be ignored. In addition to the equation of time, one also has to apply corrections due to one's distance from the local time zone meridian and summer time, if any.
The tiny increase of the mean solar day due to the slowing down of the Earth's rotation, by about 2 ms per day per century, which currently accumulates up to about 1 second every year, is not taken into account in traditional definitions of the equation of time, as it is imperceptible at the accuracy level of sundials.
Major components
Eccentricity of the Earth's orbit
 The Earth revolves around the Sun. As seen from Earth, the Sun appears to revolve once around the Earth through the background stars in one year. If the Earth orbited the Sun with a constant speed, in a circular orbit in a plane perpendicular to the Earth's axis, then the Sun would culminate every day at exactly the same time, and be a perfect time keeper (except for the very small effect of the slowing rotation of the Earth). But the orbit of the Earth is an ellipse not centered on the Sun, and its speed varies between 30.287 and 29.291 km/s, according to
The Earth revolves around the Sun. As seen from Earth, the Sun appears to revolve once around the Earth through the background stars in one year. If the Earth orbited the Sun with a constant speed, in a circular orbit in a plane perpendicular to the Earth's axis, then the Sun would culminate every day at exactly the same time, and be a perfect time keeper (except for the very small effect of the slowing rotation of the Earth). But the orbit of the Earth is an ellipse not centered on the Sun, and its speed varies between 30.287 and 29.291 km/s, according to Kepler's laws of planetary motion
In astronomy, Kepler's laws of planetary motion, published by Johannes Kepler in 1609 (except the third law, which was fully published in 1619), describe the orbits of planets around the Sun. These laws replaced circular orbits and epicycles in ...
, and its angular speed also varies, and thus the Sun appears to move faster (relative to the background stars) at perihelion
An apsis (; ) is the farthest or nearest point in the orbit of a planetary body about its primary body. The line of apsides (also called apse line, or major axis of the orbit) is the line connecting the two extreme values.
Apsides perta ...
(currently around 3 January) and slower at aphelion
An apsis (; ) is the farthest or nearest point in the orbit of a planetary body about its primary body. The line of apsides (also called apse line, or major axis of the orbit) is the line connecting the two extreme values.
Apsides perta ...
a half year later.
At these extreme points, this effect varies the apparent solar day by 7.9 s/day from its mean. Consequently, the smaller daily differences on other days in speed are cumulative until these points, reflecting how the planet accelerates and decelerates compared to the mean.
As a result, the eccentricity of the Earth's orbit contributes a periodic variation which is (in the first-order approximation) a sine wave
A sine wave, sinusoidal wave, or sinusoid (symbol: ∿) is a periodic function, periodic wave whose waveform (shape) is the trigonometric function, trigonometric sine, sine function. In mechanics, as a linear motion over time, this is ''simple ...
with:
* amplitude: 7.66 minutes
* period: one year
* zero points: perihelion (at the beginning of January) and aphelion (beginning of July)
* extreme values: early April (negative) and early October (positive)
This component of the EoT is represented by aforementioned factor ''a'':
:
Obliquity of the ecliptic
Even if the Earth's orbit were circular, the perceived motion of the Sun along ourcelestial equator
The celestial equator is the great circle of the imaginary celestial sphere on the same plane as the equator of Earth. By extension, it is also a plane of reference in the equatorial coordinate system. Due to Earth's axial tilt, the celestial ...
would still not be uniform. This is a consequence of the tilt of the Earth's rotational axis with respect to the plane of its orbit, or equivalently, the tilt of the ecliptic
The ecliptic or ecliptic plane is the orbital plane of Earth's orbit, Earth around the Sun. It was a central concept in a number of ancient sciences, providing the framework for key measurements in astronomy, astrology and calendar-making.
Fr ...
(the path the Sun appears to take in the celestial sphere
In astronomy and navigation, the celestial sphere is an abstract sphere that has an arbitrarily large radius and is concentric to Earth. All objects in the sky can be conceived as being projected upon the inner surface of the celestial sphere, ...
) with respect to the celestial equator
The celestial equator is the great circle of the imaginary celestial sphere on the same plane as the equator of Earth. By extension, it is also a plane of reference in the equatorial coordinate system. Due to Earth's axial tilt, the celestial ...
. The projection of this motion onto our celestial equator
The celestial equator is the great circle of the imaginary celestial sphere on the same plane as the equator of Earth. By extension, it is also a plane of reference in the equatorial coordinate system. Due to Earth's axial tilt, the celestial ...
, along which "clock time" is measured, is a maximum at the solstice
A solstice is the time when the Sun reaches its most northerly or southerly sun path, excursion relative to the celestial equator on the celestial sphere. Two solstices occur annually, around 20–22 June and 20–22 December. In many countries ...
s, when the yearly movement of the Sun is parallel to the equator (causing amplification of perceived speed) and yields mainly a change in right ascension
Right ascension (abbreviated RA; symbol ) is the angular distance of a particular point measured eastward along the celestial equator from the Sun at the equinox (celestial coordinates), March equinox to the (hour circle of the) point in questio ...
. It is a minimum at the equinox
A solar equinox is a moment in time when the Sun appears directly above the equator, rather than to its north or south. On the day of the equinox, the Sun appears to rise directly east and set directly west. This occurs twice each year, arou ...
es, when the Sun's apparent motion is more sloped and yields more change in declination
In astronomy, declination (abbreviated dec; symbol ''δ'') is one of the two angles that locate a point on the celestial sphere in the equatorial coordinate system, the other being hour angle. The declination angle is measured north (positive) or ...
, leaving less for the component in right ascension
Right ascension (abbreviated RA; symbol ) is the angular distance of a particular point measured eastward along the celestial equator from the Sun at the equinox (celestial coordinates), March equinox to the (hour circle of the) point in questio ...
, which is the only component that affects the duration of the solar day. A practical illustration of obliquity is that the daily shift of the shadow cast by the Sun in a sundial even on the equator is smaller close to the solstices and greater close to the equinoxes. If this effect operated alone, then days would be up to 24 hours and 20.3 seconds long (measured solar noon to solar noon) near the solstices, and as much as 20.3 seconds shorter than 24 hours near the equinoxes.
In the figure on the right, we can see the monthly variation of the apparent slope of the plane of the ecliptic at solar midday as seen from Earth. This variation is due to the apparent precession
Precession is a change in the orientation of the rotational axis of a rotating body. In an appropriate reference frame it can be defined as a change in the first Euler angle, whereas the third Euler angle defines the rotation itself. In o ...
of the rotating Earth through the year, as seen from the Sun at solar midday.
In terms of the equation of time, the inclination of the ecliptic results in the contribution of a sine wave variation with:
* amplitude: 9.87 minutes
* period: 1/2 year
* zero points: equinoxes and solstices
* extreme values: beginning of February and August (negative) and beginning of May and November (positive).
This component of the EoT is represented by the aforementioned factor "b":
Secular effects
The two above mentioned factors have different wavelengths, amplitudes and phases, so their combined contribution is an irregular wave. Atepoch
In chronology and periodization, an epoch or reference epoch is an instant in time chosen as the origin of a particular calendar era. The "epoch" serves as a reference point from which time is measured.
The moment of epoch is usually decided b ...
2000 these are the values (in minutes and seconds with UT dates):
On shorter timescales (thousands of years) the shifts in the dates of equinox and perihelion will be more important. The former is caused by precession
Precession is a change in the orientation of the rotational axis of a rotating body. In an appropriate reference frame it can be defined as a change in the first Euler angle, whereas the third Euler angle defines the rotation itself. In o ...
, and shifts the equinox backwards compared to the stars. But it can be ignored in the current discussion as our Gregorian calendar
The Gregorian calendar is the calendar used in most parts of the world. It went into effect in October 1582 following the papal bull issued by Pope Gregory XIII, which introduced it as a modification of, and replacement for, the Julian cale ...
is constructed in such a way as to keep the vernal equinox date at 20 March (at least at sufficient accuracy for our aim here). The shift of the perihelion is forwards, about 1.7 days every century. In 1246 the perihelion occurred on 22 December, the day of the solstice, so the two contributing waves had common zero points and the equation of time curve was symmetrical: in ''Astronomical Algorithms'' Meeus gives February and November extrema of 15 m 39 s and May and July ones of 4 m 58 s. Before then the February minimum was larger than the November maximum, and the May maximum larger than the July minimum. In fact, in years before −1900 (1901 BCE) the May maximum was larger than the November maximum. In the year −2000 (2001 BCE) the May maximum was +12 minutes and a couple seconds while the November maximum was just less than 10 minutes. The secular change is evident when one compares a current graph of the equation of time (see below) with one from 2000 years ago, e.g., one constructed from the data of Ptolemy.
Practical use
If thegnomon
A gnomon (; ) is the part of a sundial that casts a shadow. The term is used for a variety of purposes in mathematics and other fields, typically to measure directions, position, or time.
History
A painted stick dating from 2300 BC that was ...
(the shadow-casting object) is not an edge but a point (e.g., a hole in a plate), the shadow (or spot of light) will trace out a curve during the course of a day. If the shadow is cast on a plane surface, this curve will be a conic section
A conic section, conic or a quadratic curve is a curve obtained from a cone's surface intersecting a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, tho ...
(usually a hyperbola), since the circle of the Sun's motion together with the gnomon point define a cone. At the spring and autumnal equinoxes, the cone degenerates into a plane and the hyperbola into a line. With a different hyperbola for each day, hour marks can be put on each hyperbola which include any necessary corrections. Unfortunately, each hyperbola corresponds to two different days, one in each half of the year, and these two days will require different corrections. A convenient compromise is to draw the line for the "mean time" and add a curve showing the exact position of the shadow points at noon during the course of the year. This curve will take the form of a figure eight and is known as an analemma
In astronomy, an analemma (; ) is a diagram showing the position of the Sun in the sky as seen from a fixed location on Earth at the same Solar time#Mean solar time, mean solar time over the course of a year. The change of position is a result ...
. By comparing the analemma to the mean noon line, the amount of correction to be applied generally on that day can be determined.
The equation of time is used not only in connection with sundial
A sundial is a horology, horological device that tells the time of day (referred to as civil time in modern usage) when direct sunlight shines by the position of the Sun, apparent position of the Sun in the sky. In the narrowest sense of the ...
s and similar devices, but also for many applications of solar energy
Solar energy is the radiant energy from the Sun's sunlight, light and heat, which can be harnessed using a range of technologies such as solar electricity, solar thermal energy (including solar water heating) and solar architecture. It is a ...
. Machines such as solar trackers and heliostat
A heliostat
()
is a device that reflects sunlight toward a target, turning to compensate for the Sun's apparent motion.
The reflector is usually a plane mirror.
The target may be a physical object, distant from the heliostat, or a direct ...
s have to move in ways that are influenced by the equation of time.
Civil time
In modern usage, civil time refers to statutory time as designated by civilian authorities. Modern civil time is generally national standard time in a time zone at a UTC offset, fixed offset from Coordinated Universal Time (UTC), possibly adjusted ...
is the local mean time for a meridian that often passes near the center of the time zone
A time zone is an area which observes a uniform standard time for legal, Commerce, commercial and social purposes. Time zones tend to follow the boundaries between Country, countries and their Administrative division, subdivisions instead of ...
, and may possibly be further altered by daylight saving time
Daylight saving time (DST), also referred to as daylight savings time, daylight time (Daylight saving time in the United States, United States and Daylight saving time in Canada, Canada), or summer time (British Summer Time, United Kingdom, ...
. When the apparent solar time that corresponds to a given civil time is to be found, the difference in longitude between the site of interest and the time zone meridian, daylight saving time, and the equation of time must all be considered.
Calculation
The equation of time is obtained from a published table, or a graph. For dates in the past such tables are produced from historical measurements, or by calculation; for future dates, of course, tables can only be calculated. In devices such as computer-controlled heliostats the computer is often programmed to calculate the equation of time. The calculation can be numerical or analytical. The former are based onnumerical integration
In analysis, numerical integration comprises a broad family of algorithms for calculating the numerical value of a definite integral.
The term numerical quadrature (often abbreviated to quadrature) is more or less a synonym for "numerical integr ...
of the differential equations of motion, including all significant gravitational and relativistic effects. The results are accurate to better than 1 second and are the basis for modern almanac data. The latter are based on a solution that includes only the gravitational interaction between the Sun and Earth, simpler than but not as accurate as the former. Its accuracy can be improved by including small corrections.
The following discussion describes a reasonably accurate (agreeing with almanac data to within 3 seconds over a wide range of years) algorithm for the equation of time that is well known to astronomers. It also shows how to obtain a simple approximate formula (accurate to within 1 minute over a large time interval), that can be easily evaluated with a calculator and provides the simple explanation of the phenomenon that was used previously in this article.
Mathematical description
The precise definition of the equation of time is: : The quantities occurring in this equation are: * EOT, the time difference between apparent solar time andmean solar time
Solar time is a calculation of the passage of time based on the position of the Sun in the sky. The fundamental unit of solar time is the day, based on the synodic rotation period. Traditionally, there are three types of time reckoning based ...
;
* GHA, the Greenwich Hour Angle
In astronomy and celestial navigation, the hour angle is the dihedral angle between the '' meridian plane'' (containing Earth's axis and the zenith) and the '' hour circle'' (containing Earth's axis and a given point of interest).
It may be ...
of the apparent (actual) Sun;
* GMHA = Universal Time − Offset, the Greenwich Mean Hour Angle of the mean (fictitious) Sun.
Here time and angle are quantities that are related by factors such as: 2 radians = 360° = 1 day = 24 hours. The difference, EOT, is measurable since GHA is an angle that can be measured and Universal Time
Universal Time (UT or UT1) is a time standard based on Earth's rotation. While originally it was mean solar time at 0° longitude, precise measurements of the Sun are difficult. Therefore, UT1 is computed from a measure of the Earth's angle wi ...
, UT, is a scale for the measurement of time. The offset by = 180° = 12 hours from UT is needed because UT is zero at mean midnight while GMHA = 0 at mean noon. Universal Time is discontinuous at mean midnight so another quantity day number , an integer, is required in order to form the continuous quantity time : . Both GHA and GMHA, like all physical angles, have a mathematical, but not a physical discontinuity at their respective (apparent and mean) noon. Despite the mathematical discontinuities of its components, EOT is defined as a continuous function by adding (or subtracting) 24 hours in the small time interval between the discontinuities in GHA and GMHA.
According to the definitions of the angles on the celestial sphere (see hour angle
In astronomy and celestial navigation, the hour angle is the dihedral angle between the '' meridian plane'' (containing Earth's axis and the zenith) and the '' hour circle'' (containing Earth's axis and a given point of interest).
It may be ...
)where: * GAST is the Greenwich apparent
sidereal time
Sidereal time ("sidereal" pronounced ) is a system of timekeeping used especially by astronomers. Using sidereal time and the celestial coordinate system, it is easy to locate the positions of celestial objects in the night sky. Sidereal t ...
(the angle between the apparent vernal equinox and the meridian in the plane of the equator). This is a known function of UT.
* is the right ascension
Right ascension (abbreviated RA; symbol ) is the angular distance of a particular point measured eastward along the celestial equator from the Sun at the equinox (celestial coordinates), March equinox to the (hour circle of the) point in questio ...
of the apparent Sun (the angle between the apparent vernal equinox and the actual Sun in the plane of the equator).
On substituting into the equation of time, it is
:
Like the formula for GHA above, one can write , where the last term is the right ascension of the mean Sun. The equation is often written in these terms as
:
where . In this formulation a measurement or calculation of EOT at a certain value of time depends on a measurement or calculation of at that time. Both and vary from 0 to 24 hours during the course of a year. The former has a discontinuity at a time that depends on the value of UT, while the latter has its at a slightly later time. As a consequence, when calculated this way EOT has two, artificial, discontinuities. They can both be removed by subtracting 24 hours from the value of EOT in the small time interval after the discontinuity in and before the one in . The resulting EOT is a continuous function of time.
Another definition, denoted to distinguish it from EOT, is
:
Here , is the Greenwich mean sidereal time (the angle between the mean vernal equinox and the mean Sun in the plane of the equator). Therefore, GMST is an approximation to GAST (and is an approximation to EOT); eqeq is called the equation of the equinoxes and is due to the wobbling, or nutation of the Earth's axis of rotation about its precessional motion. Since the amplitude of the nutational motion is only about 1.2 s (18″ of longitude) the difference between EOT and can be ignored unless one is interested in subsecond accuracy.
A third definition, denoted to distinguish it from EOT and , and now called the Equation of Ephemeris Time (prior to the distinction that is now made between EOT, , and the latter was known as the equation of time) is
:
here is the ecliptic longitude of the mean Sun (the angle from the mean vernal equinox to the mean Sun in the plane of the ecliptic
The ecliptic or ecliptic plane is the orbital plane of Earth's orbit, Earth around the Sun. It was a central concept in a number of ancient sciences, providing the framework for key measurements in astronomy, astrology and calendar-making.
Fr ...
).
The difference is 1.3 s from 1960 to 2040. Therefore, over this restricted range of years is an approximation to EOT whose error is in the range 0.1 to 2.5 s depending on the longitude correction in the equation of the equinoxes; for many purposes, for example correcting a sundial, this accuracy is more than good enough.
Right ascension calculation
The right ascension, and hence the equation of time, can be calculated from Newton's two-body theory of celestial motion, in which the bodies (Earth and Sun) describe elliptical orbits about their common mass center. Using this theory, the equation of time becomes: : where the new angles that appear are: * , is themean anomaly
In celestial mechanics, the mean anomaly is the fraction of an elliptical orbit's period that has elapsed since the orbiting body passed periapsis, expressed as an angle which can be used in calculating the position of that body in the classical ...
, the angle from the periapsis
An apsis (; ) is the farthest or nearest point in the orbit of a planetary body about its primary body. The line of apsides (also called apse line, or major axis of the orbit) is the line connecting the two extreme values.
Apsides perta ...
of the elliptical orbit to the mean Sun; its range is from 0 to 2 as increases from to ;
* = days is the length of time in an anomalistic year: the time interval between two successive passages of the periapsis;
* , is the ecliptic longitude of the periapsis;
* is dynamical time, the independent variable in the theory. Here it is taken to be identical with the continuous time based on UT (see above), but in more precise calculations (of or EOT) the small difference between them must be accounted for as well as the distinction between UT1 and UTC.
* is the value of at the periapsis.
To complete the calculation three additional angles are required:
* , the Sun's eccentric anomaly
In orbital mechanics, the eccentric anomaly is an angular parameter that defines the position of a body that is moving along an elliptic Kepler orbit, the angle measured at the center of the ellipse between the orbit's periapsis and the current ...
(note that this is different from );
* , the Sun's true anomaly
In celestial mechanics, true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, as seen from the main focus ...
;
* , the Sun's true longitude on the ecliptic.
celestial sphere
In astronomy and navigation, the celestial sphere is an abstract sphere that has an arbitrarily large radius and is concentric to Earth. All objects in the sky can be conceived as being projected upon the inner surface of the celestial sphere, ...
and the Sun's elliptical orbit
In astrodynamics or celestial mechanics, an elliptical orbit or eccentric orbit is an orbit with an orbital eccentricity, eccentricity of less than 1; this includes the special case of a circular orbit, with eccentricity equal to 0. Some or ...
seen from the Earth (the same as the Earth's orbit seen from the Sun). In this figure is the obliquity, while is the eccentricity
Eccentricity or eccentric may refer to:
* Eccentricity (behavior), odd behavior on the part of a person, as opposed to being "normal"
Mathematics, science and technology Mathematics
* Off-Centre (geometry), center, in geometry
* Eccentricity (g ...
of the ellipse.
Now given a value of , one can calculate by means of the following well-known procedure:
First, given , calculate from Kepler's equation
In orbital mechanics, Kepler's equation relates various geometric properties of the orbit of a body subject to a central force.
It was derived by Johannes Kepler in 1609 in Chapter 60 of his ''Astronomia nova'', and in book V of his ''Epitome of ...
:
:
Although this equation cannot be solved exactly in closed form, values of can be obtained from infinite (power or trigonometric) series, graphical, or numerical methods. Alternatively, note that for , , and by iteration:
:
This approximation can be improved, for small , by iterating again:
: ,
and continued iteration produces successively higher order terms of the power series expansion in . For small values of (much less than 1) two or three terms of the series give a good approximation for ; the smaller , the better the approximation.
Next, knowing , calculate the true anomaly
In celestial mechanics, true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, as seen from the main focus ...
from an elliptical orbit relation
:
The correct branch of the multiple valued function to use is the one that makes a continuous function of starting from . Thus for use , and for use . At the specific value for which the argument of is infinite, use . Here is the principal branch, ; the function that is returned by calculators and computer applications. Alternatively, this function can be expressed in terms of its Taylor series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor ser ...
in , the first three terms of which are:
: .
For small this approximation (or even just the first two terms) is a good one. Combining the approximation for with this one for produces:
: .
The relation is called the equation of the center
In Two-body problem, two-body, Kepler orbit, Keplerian orbital mechanics, the equation of the center is the angular difference between the actual position of a body in its elliptic orbit, elliptical orbit and the position it would occupy if its mot ...
; the expression written here is a second-order approximation in . For the small value of that characterises the Earth's orbit this gives a very good approximation for .
Next, knowing , calculate from its definition:
:
The value of varies non-linearly with because the orbit is elliptical and not circular. From the approximation for :
: .
Finally, knowing calculate from a relation for the right triangle on the celestial sphere shown above
:
Note that the quadrant of is the same as that of , therefore reduce to the range 0 to 2 and write
: ,
where is 0 if is in quadrant 1, it is 1 if is in quadrants 2 or 3 and it is 2 if is in quadrant 4. For the values at which tan is infinite, .
Although approximate values for can be obtained from truncated Taylor series like those for , it is more efficacious to use the equation
:
where . Note that for , and iterating twice:
: .
Final calculation
The equation of time is obtained by substituting the result of the right ascension calculation into an equation of time formula. Here is used; in part because small corrections (of the order of 1 second), that would justify using , are not included, and in part because the goal is to obtain a simple analytical expression. Using two-term approximations for and allows to be written as an explicit expression of two terms, which is designated because it is a first order approximation in and in . : 1) minutes This equation was first derived by Milne, who wrote it in terms of . The numerical values written here result from using the orbital parameter values, = , = ° = radians, and = ° = radians that correspond to the epoch 1 January 2000 at 12 noon UT1. When evaluating the numerical expression for as given above, a calculator must be in radian mode to obtain correct values because the value of in the argument of the second term is written there in radians. Higher order approximations can also be written, but they necessarily have more terms. For example, the second order approximation in both and consists of five terms : 2) This approximation has the potential for high accuracy, however, in order to achieve it over a wide range of years, the parameters , , and must be allowed to vary with time. This creates additional calculational complications. Other approximations have been proposed, for example, which uses the first order equation of the center but no other approximation to determine , and which uses the second order equation of the center. The time variable, , can be written either in terms of , the number of days past perihelion, or , the number of days past a specific date and time (epoch): : 3) days days : 4) Here is the value of at the chosen date and time. For the values given here, in radians, is that measured for the actual Sun at the epoch, 1 January 2000 at 12 noon UT1, and is the number of days past that epoch. At periapsis , so solving gives = . This puts the periapsis on 4 January 2000 at 00:11:41 while the actual periapsis is, according to results from the ''Multiyear Interactive Computer Almanac'' (abbreviated as MICA), on 3 January 2000 at 05:17:30. This large discrepancy happens because the difference between the orbital radius at the two locations is only 1 part in a million; in other words, radius is a very weak function of time near periapsis. As a practical matter this means that one cannot get a highly accurate result for the equation of time by using and adding the actual periapsis date for a given year. However, high accuracy can be achieved by using the formulation in terms of .
When , ''M'' is greater than 2 and one must subtract a multiple of 2 (that depends on the year) from it to bring it into the range 0 to 2. Likewise for years prior to 2000 one must add multiples of 2. For example, for the year 2010, varies from on 1 January at noon to on 31 December at noon; the corresponding values are and and are reduced to the range 0 to 2 by subtracting 10 and 11 times 2 respectively.
One can always write:
5)
where:
* = number of days from the epoch to noon on 1 January of the desired year
* (365 if the calculation is for a leap year).
The resulting equation for years after 2000, written as a sum of two terms, given 1), 4) and 5), is:
6) inutes
In plain text format:
7) EoT = -7.659sin(6.24004077 + 0.01720197(365*(y-2000) + d)) + 9.863sin( 2 (6.24004077 + 0.01720197 (365*(y-2000) + d)) + 3.5932 ) inutes
Term "a" represents the contribution of eccentricity, term "b" represents contribution of obliquity.
The result of the computations is usually given as either a set of tabular values, or a graph of the equation of time as a function of . A comparison of plots of , , and results from MICA all for the year 2000 is shown in the figure. The plot of is seen to be close to the results produced by MICA, the absolute error, , is less than 1 minute throughout the year; its largest value is 43.2 seconds and occurs on day 276 (3 October). The plot of is indistinguishable from the results of MICA, the largest absolute error between the two is 2.46 s on day 324 (20 November).
Here is the value of at the chosen date and time. For the values given here, in radians, is that measured for the actual Sun at the epoch, 1 January 2000 at 12 noon UT1, and is the number of days past that epoch. At periapsis , so solving gives = . This puts the periapsis on 4 January 2000 at 00:11:41 while the actual periapsis is, according to results from the ''Multiyear Interactive Computer Almanac'' (abbreviated as MICA), on 3 January 2000 at 05:17:30. This large discrepancy happens because the difference between the orbital radius at the two locations is only 1 part in a million; in other words, radius is a very weak function of time near periapsis. As a practical matter this means that one cannot get a highly accurate result for the equation of time by using and adding the actual periapsis date for a given year. However, high accuracy can be achieved by using the formulation in terms of .
When , ''M'' is greater than 2 and one must subtract a multiple of 2 (that depends on the year) from it to bring it into the range 0 to 2. Likewise for years prior to 2000 one must add multiples of 2. For example, for the year 2010, varies from on 1 January at noon to on 31 December at noon; the corresponding values are and and are reduced to the range 0 to 2 by subtracting 10 and 11 times 2 respectively.
One can always write:
5)
where:
* = number of days from the epoch to noon on 1 January of the desired year
* (365 if the calculation is for a leap year).
The resulting equation for years after 2000, written as a sum of two terms, given 1), 4) and 5), is:
6) inutes
In plain text format:
7) EoT = -7.659sin(6.24004077 + 0.01720197(365*(y-2000) + d)) + 9.863sin( 2 (6.24004077 + 0.01720197 (365*(y-2000) + d)) + 3.5932 ) inutes
Term "a" represents the contribution of eccentricity, term "b" represents contribution of obliquity.
The result of the computations is usually given as either a set of tabular values, or a graph of the equation of time as a function of . A comparison of plots of , , and results from MICA all for the year 2000 is shown in the figure. The plot of is seen to be close to the results produced by MICA, the absolute error, , is less than 1 minute throughout the year; its largest value is 43.2 seconds and occurs on day 276 (3 October). The plot of is indistinguishable from the results of MICA, the largest absolute error between the two is 2.46 s on day 324 (20 November).
Continuity
For the choice of the appropriate branch of the relation with respect to function continuity a modified version of the arctangent function is helpful. It brings in previous knowledge about the expected value by a parameter. The modified arctangent function is defined as: : . It produces a value that is as close to as possible. The function rounds to the nearest integer. Applying this yields: : . The parameter arranges here to set to the zero nearest value which is the desired one.Secular change
The difference between the MICA and results was checked every 5 years over the range from 1960 to 2040. In every instance the maximum absolute error was less than 3 s; the largest difference, 2.91 s, occurred on 22 May 1965 (day 141). However, in order to achieve this level of accuracy over this range of years it is necessary to account for the secular change in the orbital parameters with time. The equations that describe this variation are: : According to these relations, in 100 years ( = ), increases by about 0.5% (1.7°), decreases by about 0.25%, and decreases by about 0.05%. As a result, the number of calculations required for any of the higher-order approximations of the equation of time requires a computer to complete them, if one wants to achieve their inherent accuracy over a wide range of time. In this event it is no more difficult to evaluate using a computer than any of its approximations. In all this note that as written above is easy to evaluate, even with a calculator, is accurate enough (better than 1 minute over the 80-year range) for correcting sundials, and has the nice physical explanation as the sum of two terms, one due to obliquity and the other to eccentricity that was used previously in the article. This is not true either for considered as a function of or for any of its higher-order approximations.Alternative calculation
Another procedure for calculating the equation of time can be done as follows. Angles are in degrees; the conventionalorder of operations
In mathematics and computer programming, the order of operations is a collection of rules that reflect conventions about which operations to perform first in order to evaluate a given mathematical expression.
These rules are formalized with a ...
applies.
: =
where is the Earth's mean angular orbital velocity in degrees per day, a.k.a. ''"the mean daily motion"''.
:
where is the date, counted in days starting at 1 on 1 January (i.e. the days part of the ordinal date
An ordinal date is a calendar date typically consisting of a ''year'' and an ''ordinal number'', ranging between 1 and 366 (starting on January 1), representing the multiples of a ''day'', called day of the year or ordinal day number (also know ...
in the year). 9 is the approximate number of days from the December solstice to 31 December. is the angle the Earth ''would'' move on its orbit at its average speed from the December solstice to date .
:
is the angle the Earth moves from the solstice to date , including a first-order correction for the Earth's orbital eccentricity, 0.0167 . The number 3 is the approximate number of days from 31 December to the current date of the Earth's perihelion
An apsis (; ) is the farthest or nearest point in the orbit of a planetary body about its primary body. The line of apsides (also called apse line, or major axis of the orbit) is the line connecting the two extreme values.
Apsides perta ...
. This expression for can be simplified by combining constants to:
: .
:
Here, is the difference between the angle moved at mean speed, and at the angle at the corrected speed projected onto the equatorial plane, and divided by 180° to get the difference in " half-turns". The value 23.44° is the tilt of the Earth's axis ("obliquity"). The subtraction gives the conventional sign to the equation of time. For any given value of , (sometimes written as ) has multiple values, differing from each other by integer numbers of half turns. The value generated by a calculator or computer may not be the appropriate one for this calculation. This may cause to be wrong by an integer number of half-turns. The excess half-turns are removed in the next step of the calculation to give the equation of time:
: minutes
The expression means the ''nearest integer'' to . On a computer, it can be programmed, for example, as . Its value is 0, 1, or 2 at different times of the year. Subtracting it leaves a small positive or negative fractional number of half turns, which is multiplied by 720, the number of minutes (12 hours) that the Earth takes to rotate one half turn relative to the Sun, to get the equation of time.
Compared with published values, this calculation has a root mean square
In mathematics, the root mean square (abbrev. RMS, or rms) of a set of values is the square root of the set's mean square.
Given a set x_i, its RMS is denoted as either x_\mathrm or \mathrm_x. The RMS is also known as the quadratic mean (denote ...
error of only 3.7 s. The greatest error is 6.0 s. This is much more accurate than the approximation described above, but not as accurate as the elaborate calculation.
Solar declination
The value of in the above calculation is an accurate value for the Sun's ecliptic longitude (shifted by 90°), so the solar declination becomes readily available: : which is accurate to within a fraction of a degree.See also
* *Notes
References
* * *External links
NOAA Solar Calculator
* (include rise/set/transit times of the Sun and other celestial objects)
The equation of time
described on the
Royal Greenwich Observatory
The Royal Observatory, Greenwich (ROG; known as the Old Royal Observatory from 1957 to 1998, when the working Royal Greenwich Observatory, RGO, temporarily moved south from Greenwich to Herstmonceux) is an observatory situated on a hill in G ...
web site
The Equation of Time and the Analemma
by Kieron Taylor
containing a link to a C program using a more accurate formula than most (particularly at high inclinations and eccentricities). The program can calculate solar declination, Equation of Time, or Analemma
* ttps://web.archive.org/web/20140318064248/http://www.pendulumofmayfair.co.uk/view.asp?pid=272&cat=Longcase%20Clocks Equation of Time Longcase Clock by John Topping C.1720
The equation of time correction-table
A page describing how to correct a clock to a sundial
Calculate your solar time, including the equation of time {{DEFAULTSORT:Equation of Time Dynamics of the Solar System Timekeeping Time in astronomy Earth phenomena Sundials Equations