Elastic deformation on:
[Wikipedia]
[Google]
[Amazon]
In engineering, deformation refers to the change in size or shape of an object. ''Displacements'' are the ''absolute'' change in position of a point on the object. Deflection is the relative change in external displacements on an object. Strain is the ''relative'' internal change in shape of an infinitesimally small cube of material and can be expressed as a non-dimensional change in length or angle of distortion of the cube. Strains are related to the forces acting on the cube, which are known as stress, by a stress-strain curve. The relationship between stress and strain is generally linear and reversible up until the yield point and the deformation is elastic. The linear relationship for a material is known as Young's modulus. Above the yield point, some degree of permanent distortion remains after unloading and is termed plastic deformation. The determination of the stress and strain throughout a solid object is given by the field of strength of materials and for a structure by
 Where is constant related to the material flow stress. indicates the derivative of strain by the time, which is also known as strain rate. is the strain-rate sensitivity. Moreover, value of is related to the resistance toward the necking. Usually, the value of is at the range of 0-0.1 at room temperature and as high as 0.8 when the temperature is increased.
By combining the 1) and 2), we can create the ultimate relation as below:
:
Where is the global constant for relating strain, strain rate and stress.
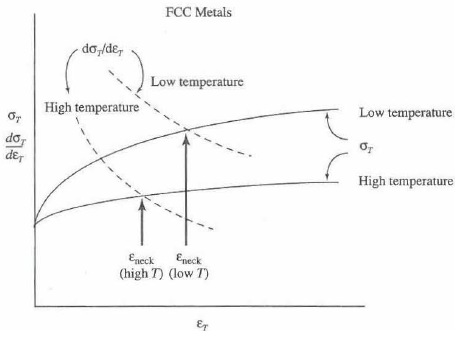
3) Based on the true stress-strain curve and its derivative form, we can estimate the strain necessary to start necking. This can be calculated based on the intersection between true stress-strain curve as shown in right.
This figure also shows the dependency of the necking strain at different temperature. In case of FCC metals, both of the stress-strain curve at its derivative are highly dependent on temperature. Therefore, at higher temperature, necking starts to appear even under lower strain value.
All of these properties indicate the importance of calculating the true stress-strain curve for further analyzing the behavior of materials in sudden environment.
4) A graphical method, so-called "Considere construction", can help determine the behavior of stress-strain curve whether necking or drawing happens on the sample. By setting as determinant, the true stress and strain can be expressed with engineering stress and strain as below:
:
Therefore, the value of engineering stress can be expressed by the secant line from made by true stress and value where to . By analyzing the shape of diagram and secant line, we can determine whether the materials show drawing or necking.
Where is constant related to the material flow stress. indicates the derivative of strain by the time, which is also known as strain rate. is the strain-rate sensitivity. Moreover, value of is related to the resistance toward the necking. Usually, the value of is at the range of 0-0.1 at room temperature and as high as 0.8 when the temperature is increased.
By combining the 1) and 2), we can create the ultimate relation as below:
:
Where is the global constant for relating strain, strain rate and stress.
3) Based on the true stress-strain curve and its derivative form, we can estimate the strain necessary to start necking. This can be calculated based on the intersection between true stress-strain curve as shown in right.
This figure also shows the dependency of the necking strain at different temperature. In case of FCC metals, both of the stress-strain curve at its derivative are highly dependent on temperature. Therefore, at higher temperature, necking starts to appear even under lower strain value.
All of these properties indicate the importance of calculating the true stress-strain curve for further analyzing the behavior of materials in sudden environment.
4) A graphical method, so-called "Considere construction", can help determine the behavior of stress-strain curve whether necking or drawing happens on the sample. By setting as determinant, the true stress and strain can be expressed with engineering stress and strain as below:
:
Therefore, the value of engineering stress can be expressed by the secant line from made by true stress and value where to . By analyzing the shape of diagram and secant line, we can determine whether the materials show drawing or necking.
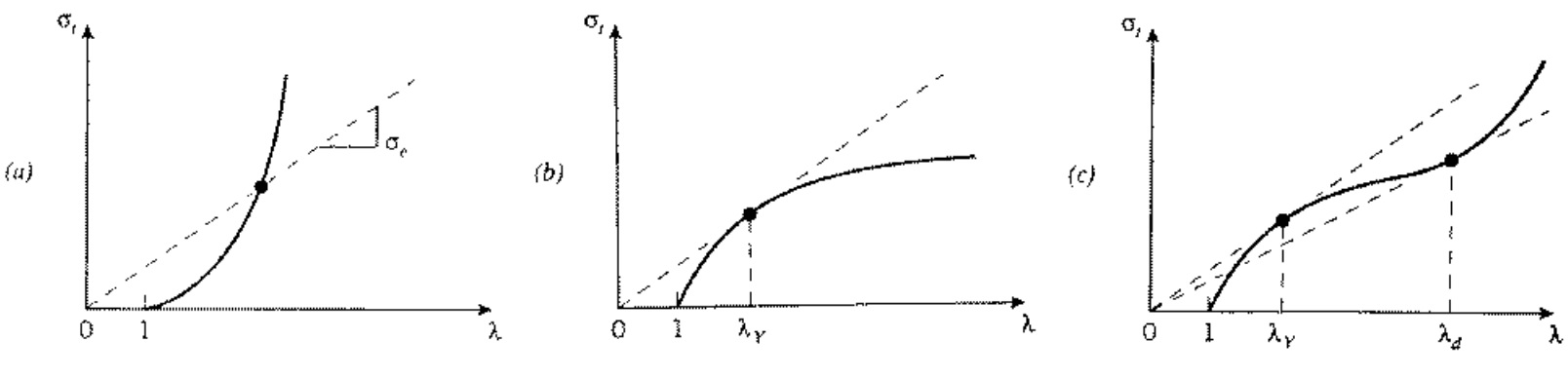 On the figure (a), there is only concave upward Considere plot. It indicates that there is no yield drop so the material will be suffered from fracture before it yields. On the figure (b), there is specific point where the tangent matches with secant line at point where . After this value, the slope becomes smaller than the secant line where necking starts to appear. On the figure (c), there is point where yielding starts to appear but when , the drawing happens. After drawing, all the material will stretch and eventually show fracture. Between and , the material itself does not stretch but rather, only the neck starts to stretch out.
On the figure (a), there is only concave upward Considere plot. It indicates that there is no yield drop so the material will be suffered from fracture before it yields. On the figure (b), there is specific point where the tangent matches with secant line at point where . After this value, the slope becomes smaller than the secant line where necking starts to appear. On the figure (c), there is point where yielding starts to appear but when , the drawing happens. After drawing, all the material will stretch and eventually show fracture. Between and , the material itself does not stretch but rather, only the neck starts to stretch out.

structural analysis
Structural analysis is a branch of Solid Mechanics which uses simplified models for solids like bars, beams and shells for engineering decision making. Its main objective is to determine the effect of loads on the physical structures and thei ...
.
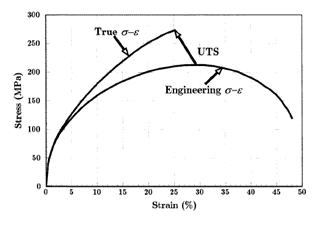
Engineering stress and engineering strain are approximations to the internal state that may be determined from the external forces and deformations of an object, provided that there is no significant change in size. When there is a significant change in size, the true stress and true strain can be derived from the instantaneous size of the object.
In the figure it can be seen that the compressive loading (indicated by the arrow) has caused deformation in the cylinder so that the original shape (dashed lines) has changed (deformed) into one with bulging sides. The sides bulge because the material, although strong enough to not crack or otherwise fail, is not strong enough to support the load without change. As a result, the material is forced out laterally. Internal forces (in this case at right angles to the deformation) resist the applied load.
The concept of a rigid body can be applied if the deformation is negligible.
Types of deformation
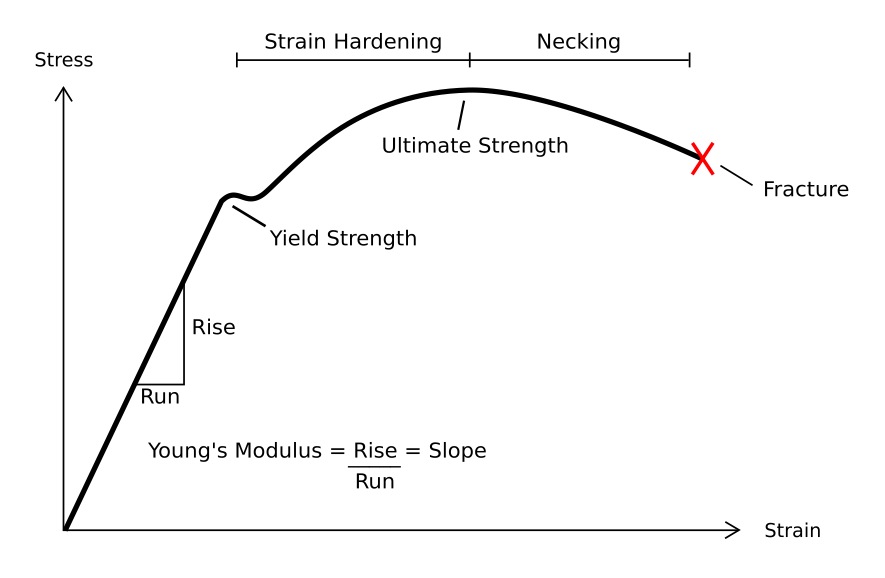
Depending on the type of material, size and geometry of the object, and the forces applied, various types of deformation may result. The image to the right shows the engineering stress vs. strain diagram for a typical ductile material such as steel. Different deformation modes may occur under different conditions, as can be depicted using adeformation mechanism map
A deformation mechanism, in geology, is a process occurring at a microscopic scale that is responsible for changes in a material's internal structure, shape and volume. The process involves planar discontinuity and/or displacement of atoms from th ...
.
Permanent deformation is irreversible; the deformation stays even after removal of the applied forces, while the temporary deformation is recoverable as it disappears after the removal of applied forces.
Temporary deformation is also called elastic deformation, while the permanent deformation is called plastic deformation.

Elastic deformation
The study of temporary or elastic deformation in the case ofengineering strain
In engineering, deformation refers to the change in size or shape of an object. ''Displacements'' are the ''absolute'' change in position of a point on the object. Deflection is the relative change in external displacements on an object. Strain ...
is applied to materials used in mechanical and structural engineering, such as concrete and steel
Steel is an alloy made up of iron with added carbon to improve its strength and fracture resistance compared to other forms of iron. Many other elements may be present or added. Stainless steels that are corrosion- and oxidation-resistant ty ...
, which are subjected to very small deformations. Engineering strain is modeled by infinitesimal strain theory, also called ''small strain theory'', ''small deformation theory'', ''small displacement theory'', or ''small displacement-gradient theory'' where strains and rotations are both small.
For some materials, e.g. elastomers and polymers, subjected to large deformations, the engineering definition of strain is not applicable, e.g. typical engineering strains greater than 1%, thus other more complex definitions of strain are required, such as ''stretch'', ''logarithmic strain'', ''Green strain'', and ''Almansi strain''. Elastomer
An elastomer is a polymer with viscoelasticity (i.e. both viscosity and elasticity) and with weak intermolecular forces, generally low Young's modulus and high failure strain compared with other materials. The term, a portmanteau of ''elastic p ...
s and shape memory metals such as Nitinol exhibit large elastic deformation ranges, as does rubber. However, elasticity is nonlinear in these materials.
Normal metals, ceramics and most crystals show linear elasticity and a smaller elastic range.
Linear elastic deformation is governed by Hooke's law, which states:
:
Where is the applied stress, is a material constant called Young's modulus or elastic modulus, and ε is the resulting strain. This relationship only applies in the elastic range and indicates that the slope of the stress vs. strain curve can be used to find Young's modulus (). Engineers often use this calculation in tensile tests.
Note that not all elastic materials undergo linear elastic deformation; some, such as concrete, gray cast iron, and many polymers, respond in a nonlinear fashion. For these materials Hooke's law is inapplicable.

True stress and strain
Since we disregard the change of area during deformation above, the true stress and strain curve should be re-derived. For deriving the stress strain curve, we can assume that the volume change is 0 even if we deformed the materials. We can assume that: : Then, the true stress can be expressed as below: : Additionally, the true strain εT can be express as below: : Then, we can express the value as : Thus, we can induce the plot in terms of and as right figure. Additionally, based on the true stress-strain curve, we can estimate the region where necking starts to happen. Since necking starts to appear after ultimate tensile stress where the maximum force applied, we can express this situation as below: : so this form can be expressed as below: : It indicates that the necking starts to appear where reduction of area becomes much significant compared to the stress change. Then the stress will be localized to specific area where the necking appears. Additionally, we can induce various relation based on true stress-strain curve. 1) True strain and stress curve can be expressed by the approximate linear relationship by taking a log on true stress and strain. The relation can be expressed as below: : Where is stress coefficient and is strain-hardening coefficient. Usually, the value of has range around 0.02 to 0.5 at room temperature. If is 1, we can express this material as perfect elastic material. 2) In reality, stress is also highly dependent on the rate of strain variation. Thus, we can induce the empirical equation based on the strain rate variation. : Where is constant related to the material flow stress. indicates the derivative of strain by the time, which is also known as strain rate. is the strain-rate sensitivity. Moreover, value of is related to the resistance toward the necking. Usually, the value of is at the range of 0-0.1 at room temperature and as high as 0.8 when the temperature is increased.
By combining the 1) and 2), we can create the ultimate relation as below:
:
Where is the global constant for relating strain, strain rate and stress.
3) Based on the true stress-strain curve and its derivative form, we can estimate the strain necessary to start necking. This can be calculated based on the intersection between true stress-strain curve as shown in right.
This figure also shows the dependency of the necking strain at different temperature. In case of FCC metals, both of the stress-strain curve at its derivative are highly dependent on temperature. Therefore, at higher temperature, necking starts to appear even under lower strain value.
All of these properties indicate the importance of calculating the true stress-strain curve for further analyzing the behavior of materials in sudden environment.
4) A graphical method, so-called "Considere construction", can help determine the behavior of stress-strain curve whether necking or drawing happens on the sample. By setting as determinant, the true stress and strain can be expressed with engineering stress and strain as below:
:
Therefore, the value of engineering stress can be expressed by the secant line from made by true stress and value where to . By analyzing the shape of diagram and secant line, we can determine whether the materials show drawing or necking.
Where is constant related to the material flow stress. indicates the derivative of strain by the time, which is also known as strain rate. is the strain-rate sensitivity. Moreover, value of is related to the resistance toward the necking. Usually, the value of is at the range of 0-0.1 at room temperature and as high as 0.8 when the temperature is increased.
By combining the 1) and 2), we can create the ultimate relation as below:
:
Where is the global constant for relating strain, strain rate and stress.
3) Based on the true stress-strain curve and its derivative form, we can estimate the strain necessary to start necking. This can be calculated based on the intersection between true stress-strain curve as shown in right.
This figure also shows the dependency of the necking strain at different temperature. In case of FCC metals, both of the stress-strain curve at its derivative are highly dependent on temperature. Therefore, at higher temperature, necking starts to appear even under lower strain value.
All of these properties indicate the importance of calculating the true stress-strain curve for further analyzing the behavior of materials in sudden environment.
4) A graphical method, so-called "Considere construction", can help determine the behavior of stress-strain curve whether necking or drawing happens on the sample. By setting as determinant, the true stress and strain can be expressed with engineering stress and strain as below:
:
Therefore, the value of engineering stress can be expressed by the secant line from made by true stress and value where to . By analyzing the shape of diagram and secant line, we can determine whether the materials show drawing or necking.
 On the figure (a), there is only concave upward Considere plot. It indicates that there is no yield drop so the material will be suffered from fracture before it yields. On the figure (b), there is specific point where the tangent matches with secant line at point where . After this value, the slope becomes smaller than the secant line where necking starts to appear. On the figure (c), there is point where yielding starts to appear but when , the drawing happens. After drawing, all the material will stretch and eventually show fracture. Between and , the material itself does not stretch but rather, only the neck starts to stretch out.
On the figure (a), there is only concave upward Considere plot. It indicates that there is no yield drop so the material will be suffered from fracture before it yields. On the figure (b), there is specific point where the tangent matches with secant line at point where . After this value, the slope becomes smaller than the secant line where necking starts to appear. On the figure (c), there is point where yielding starts to appear but when , the drawing happens. After drawing, all the material will stretch and eventually show fracture. Between and , the material itself does not stretch but rather, only the neck starts to stretch out.
Plastic deformation
This type of deformation is not undone simply by removing the applied force. An object in the plastic deformation range, however, will first have undergone elastic deformation, which is undone simply be removing the applied force, so the object will return part way to its original shape. Softthermoplastics
A thermoplastic, or thermosoft plastic, is any plastic polymer material that becomes pliable or moldable at a certain elevated temperature and solidifies upon cooling.
Most thermoplastics have a high molecular weight. The polymer chains associate ...
have a rather large plastic deformation range as do ductile metals such as copper, silver, and gold. Steel
Steel is an alloy made up of iron with added carbon to improve its strength and fracture resistance compared to other forms of iron. Many other elements may be present or added. Stainless steels that are corrosion- and oxidation-resistant ty ...
does, too, but not cast iron. Hard thermosetting plastics, rubber, crystals, and ceramics have minimal plastic deformation ranges. An example of a material with a large plastic deformation range is wet chewing gum, which can be stretched to dozens of times its original length.
Under tensile stress, plastic deformation is characterized by a strain hardening region and a necking region and finally, fracture (also called rupture). During strain hardening the material becomes stronger through the movement of atomic dislocations. The necking phase is indicated by a reduction in cross-sectional area of the specimen. Necking begins after the ultimate strength is reached. During necking, the material can no longer withstand the maximum stress and the strain in the specimen rapidly increases. Plastic deformation ends with the fracture of the material.
Compressive failure
Usually, compressive stress applied to bars,column
A column or pillar in architecture and structural engineering is a structural element that transmits, through compression, the weight of the structure above to other structural elements below. In other words, a column is a compression member. ...
s, etc. leads to shortening.
Loading a structural element or specimen will increase the compressive stress until it reaches its compressive strength
In mechanics, compressive strength or compression strength is the capacity of a material or structure to withstand loads tending to reduce size (as opposed to tensile strength which withstands loads tending to elongate). In other words, compre ...
. According to the properties of the material, failure modes are yielding for materials with ductile behavior (most metals, some soils and plastics) or rupturing for brittle behavior (geomaterials, cast iron, glass, etc.).
In long, slender structural elements — such as columns or truss bars — an increase of compressive