effective temperature

The effective temperature of a body such as a star or planet is the temperature of a black body that would emit the same total amount of electromagnetic radiation. Effective temperature is often used as an estimate of a body's surface temperature when the body's emissivity curve (as a function of wavelength) is not known.

When the star's or planet's net emissivity in the relevant wavelength band is less than unity (less than that of a black body), the actual temperature of the body will be higher than the effective temperature. The net emissivity may be low due to surface or atmospheric properties, such as the greenhouse effect.

Star

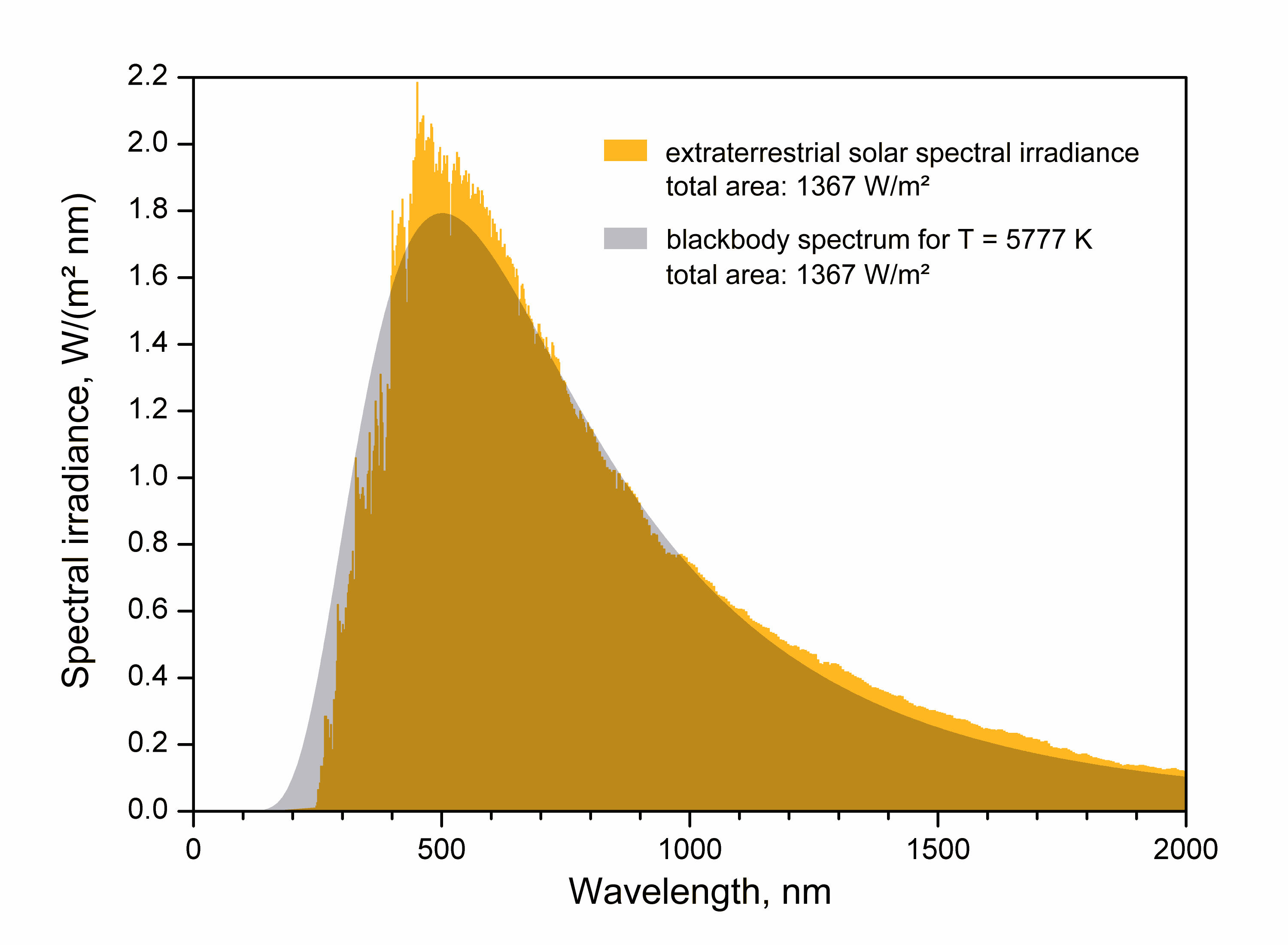
The effective temperature of a star is the temperature of a black body with the same luminosity per ''surface area'' () as the star and is defined according to the Stefan–Boltzmann law . Notice that the total ( bolometric) luminosity of a star is then , where is the stellar radius. The definition of the stellar radius is obviously not straightforward. More rigorously the effective temperature corresponds to the temperature at the radius that is defined by a certain value of the Rosseland optical depth (usually 1) within the stellar atmosphere. The effective temperature and the bolometric luminosity are the two fundamental physical parameters needed to place a star on the Hertzsprung–Russell diagram. Both effective temperature and bolometric luminosity depend on the chemical composition of a star.

The effective temperature of the Sun is around .
The nominal value defined by the International Astronomical Union for use as a unit of measure of temperature is .
Stars have a decreasing temperature gradient, going from their central core up to the atmosphere. The "core temperature" of the Sun—the temperature at the centre of the Sun where nuclear reactions take place—is estimated to be 15,000,000 K.

The color index of a star indicates its temperature from the very cool—by stellar standards—red M stars that radiate heavily in the infrared to the very hot blue O stars that radiate largely in the ultraviolet. Various colour-effective temperature relations exist in the literature. Their relations also have smaller dependencies on other stellar parameters, such as the stellar metallicity and surface gravity. The effective temperature of a star indicates the amount of heat that the star radiates per unit of surface area. From the hottest surfaces to the coolest is the sequence of stellar classifications known as O, B, A, F, G, K, M.

A red star could be a tiny red dwarf, a star of feeble energy production and a small surface or a bloated giant or even supergiant star such as Antares or Betelgeuse, either of which generates far greater energy but passes it through a surface so large that the star radiates little per unit of surface area. A star near the middle of the spectrum, such as the modest Sun or the giant Capella radiates more energy per unit of surface area than the feeble red dwarf stars or the bloated supergiants, but much less than such a white or blue star as Vega or Rigel.

Planet

Blackbody temperature

To find the effective (blackbody) temperature of a planet, it can be calculated by equating the power received by the planet to the known power emitted by a blackbody of temperature .

Take the case of a planet at a distance from the star, of luminosity .

Assuming the star radiates isotropically and that the planet is a long way from the star, the power absorbed by the planet is given by treating the planet as a disc of radius , which intercepts some of the power which is spread over the surface of a sphere of radius (the distance of the planet from the star). The calculation assumes the planet reflects some of the incoming radiation by incorporating a parameter called the albedo (a). An albedo of 1 means that all the radiation is reflected, an albedo of 0 means all of it is absorbed. The expression for absorbed power is then:

:$P_ = \frac$

The next assumption we can make is that the entire planet is at the same temperature , and that the planet radiates as a blackbody. The Stefan–Boltzmann law gives an expression for the power radiated by the planet:

:$P_ = 4 \pi r^2 \sigma T^4$

Equating these two expressions and rearranging gives an expression for the effective temperature:

:T = \sqrt /math>

Where $\sigma$ is the Stefan–Boltzmann constant. Note that the planet's radius has cancelled out of the final expression.

The effective temperature for Jupiter from this calculation is 88 K and 51 Pegasi b (Bellerophon) is 1,258 K. A better estimate of effective temperature for some planets, such as Jupiter, would need to include the internal heating as a power input. The actual temperature depends on albedo and atmosphere effects. The actual temperature from spectroscopic analysis for HD 209458 b (Osiris) is 1,130 K, but the effective temperature is 1,359 K. The internal heating within Jupiter raises the effective temperature to about 152 K.

Surface temperature of a planet

The surface temperature of a planet can be estimated by modifying the effective-temperature calculation to account for emissivity and temperature variation.

The area of the planet that absorbs the power from the star is which is some fraction of the total surface area , where is the radius of the planet. This area intercepts some of the power which is spread over the surface of a sphere of radius . We also allow the planet to reflect some of the incoming radiation by incorporating a parameter called the albedo. An albedo of 1 means that all the radiation is reflected, an albedo of 0 means all of it is absorbed. The expression for absorbed power is then:

:$P_ = \frac$

The next assumption we can make is that although the entire planet is not at the same temperature, it will radiate as if it had a temperature over an area which is again some fraction of the total area of the planet. There is also a factor , which is the emissivity and represents atmospheric effects. ranges from 1 to 0 with 1 meaning the planet is a perfect blackbody and emits all the incident power. The Stefan–Boltzmann law gives an expression for the power radiated by the planet:

:$P_ = A_ \varepsilon \sigma T^4$

Equating these two expressions and rearranging gives an expression for the surface temperature:

:T = \sqrt /math>

Note the ratio of the two areas. Common assumptions for this ratio are for a rapidly rotating body and for a slowly rotating body, or a tidally locked body on the sunlit side. This ratio would be 1 for the subsolar point, the point on the planet directly below the sun and gives the maximum temperature of the planet — a factor of (1.414) greater than the effective temperature of a rapidly rotating planet.

Also note here that this equation does not take into account any effects from internal heating of the planet, which can arise directly from sources such as radioactive decay and also be produced from frictions resulting from tidal forces.

Earth effective temperature

Earth has an albedo of about 0.306 and a solar irradiance () of at its mean orbital radius of 1.5×10⁸ km. The calculation with ε=1 and remaining physical constants then gives an Earth effective temperature of .

The actual temperature of Earth's surface is an average as of 2020. The difference between the two values is called the '' greenhouse effect''. The greenhouse effect results from materials in the atmosphere ( greenhouse gases and clouds) absorbing thermal radiation and reducing emissions to space, i.e., reducing the planet's emissivity of thermal radiation from its surface into space. Substituting the surface temperature into the equation and solving for ε gives an effective emissivity of about 0.61 for a 288 K Earth. Furthermore, these values calculate an outgoing thermal radiation flux of (with ε=0.61 as viewed from space) versus a surface thermal radiation flux of (with ε≈1 at the surface). Both fluxes are near the confidence ranges reported by the IPCC.

See also

*
*
*
*

References

External links

Effective temperature scale for solar type stars

Surface Temperature of Planets


(updated version - )

{{DEFAULTSORT:Effective Temperature
Concepts in astrophysics
Stellar astronomy
Planetary science
Thermodynamic properties
Electromagnetic radiation
Concepts in astronomy