Directional stability on:
[Wikipedia]
[Google]
[Amazon]
Directional stability is the tendency of a vehicle
or moving body to keep its orientation aligned with its direction of movement. When a car or an airplane gets turned a little relative to its direction of motion, it might correct itself, over-correct itself, or it might start to spin out of control. If it tends to correct itself, we say it's directionally stable, while if it tends to spin-out, we
say it is directionally unstable. There are many factors that can effect dynamic stability including speed, weather
and road conditions, vehicle shape and mass distribution, and tire properties.
Vehicle oscillations associated with
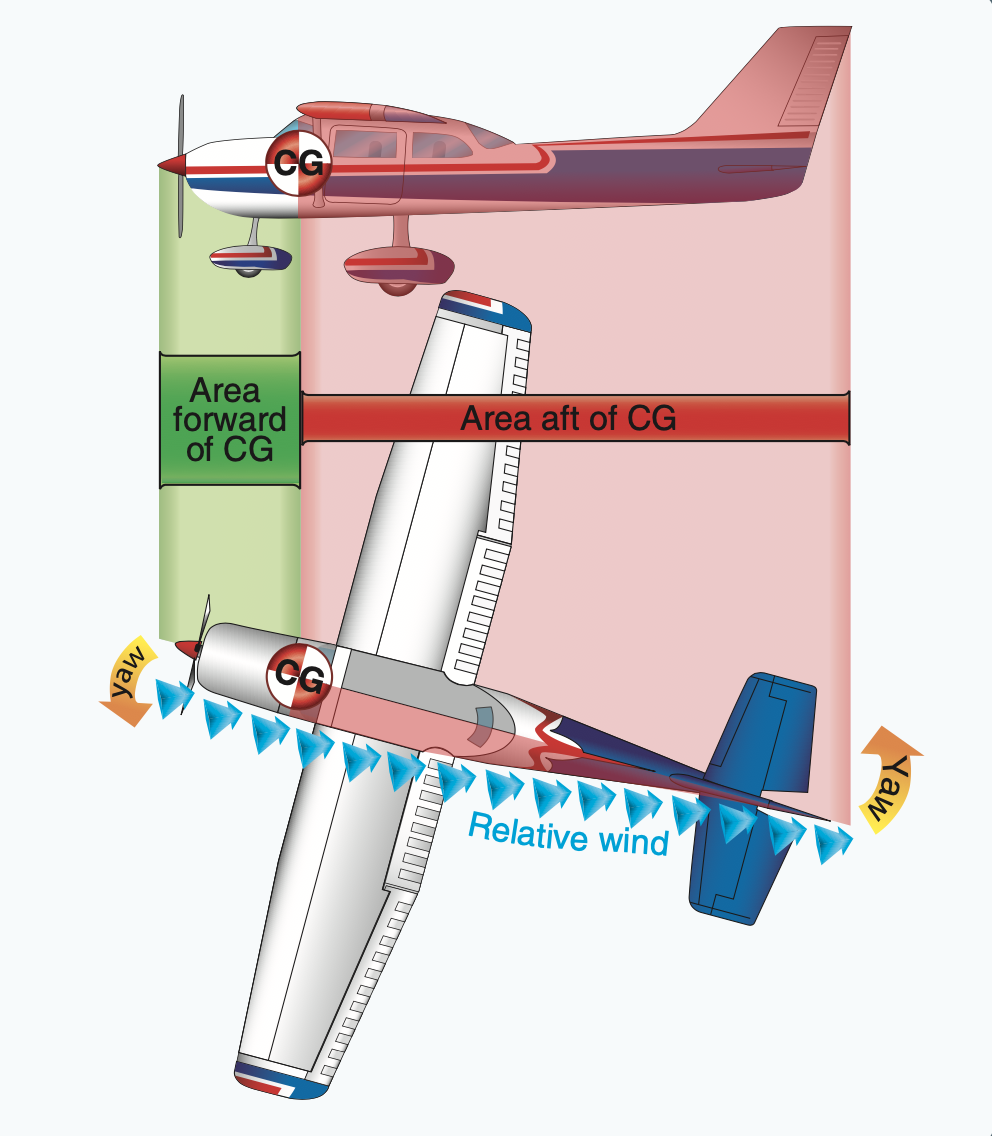 Directional stability about the aircraft's vertical axis is also referred to as yawing. This is primarily achieved by the area of the
Directional stability about the aircraft's vertical axis is also referred to as yawing. This is primarily achieved by the area of the
dynamic stability
Dynamics (from Greek δυναμικός ''dynamikos'' "powerful", from δύναμις ''dynamis'' " power") or dynamic may refer to:
Physics and engineering
* Dynamics (mechanics), the study of forces and their effect on motion
Brands and ente ...
are frequently called "weather vaning".
When the vehicle's orientation is perturbed from the direction of motion, a restoring moment may be produced which is in a direction ''opposite'' to the orientation disturbance. This can lead to oscillations in orientation around the center of mass similar to a weather vane rotating about its (vertical) pivot.
With the exception of spacecraft, vehicles generally have a recognisable front and rear and are designed so that the front points more or less in the direction of motion. Without this stability, they may tumble end over end, spin or orient themselves at a high angle of attack
In fluid dynamics, angle of attack (AOA, α, or \alpha) is the angle between a Airfoil#Airfoil terminology, reference line on a body (often the chord (aircraft), chord line of an airfoil) and the vector (geometry), vector representing the relat ...
, even broadside on to the direction of motion. At high angles of attack, drag force
In physics, a force is an influence that can cause an Physical object, object to change its velocity unless counterbalanced by other forces. In mechanics, force makes ideas like 'pushing' or 'pulling' mathematically precise. Because the Magnitu ...
s may become excessive, the vehicle may be impossible to control, or may even experience structural failure. In general, land, sea, air and underwater vehicles are designed to have a natural tendency to point in the direction of motion.
Example: road vehicle
Arrows, darts, rockets, and airships have tail surfaces (fins or feathers) to achieve directional stability; an airplane uses itsvertical stabilizer
A vertical stabilizer or tail fin is the static part of the vertical tail of an aircraft. The term is commonly applied to the assembly of both this fixed surface and one or more movable rudders hinged to it. Their role is to provide control, sta ...
for the same purpose. A road vehicle does not have elements specifically designed to maintain stability, but relies primarily on the distribution of mass
Mass is an Intrinsic and extrinsic properties, intrinsic property of a physical body, body. It was traditionally believed to be related to the physical quantity, quantity of matter in a body, until the discovery of the atom and particle physi ...
.
Introduction
These points are best illustrated with an example. The first stage of studying the stability of a road vehicle is the derivation of a reasonable approximation to the equations of motion. The diagram illustrates a four-wheel vehicle, in which the front axle is located a distance ahead of the centre of gravity and the rear axle is a distance aft of the cg. The body of the car is pointing in a direction (theta) whilst it is travelling in a direction (psi). In general, these are not the same. The tyre treads at the region of contact point in the direction of travel, but the hubs are aligned with the vehicle body, with thesteering
Steering is the control of the direction of motion or the components that enable its control. Steering is achieved through various arrangements, among them ailerons for airplanes, rudders for boats, cylic tilting of rotors for helicopters, ...
held central. The tyres distort as they rotate to accommodate this mis-alignment, and generate side forces as a consequence.
The net side force Y on the vehicle is the centripetal force causing the vehicle to change the direction it is traveling:
:
where M is the vehicle mass
Mass is an Intrinsic and extrinsic properties, intrinsic property of a physical body, body. It was traditionally believed to be related to the physical quantity, quantity of matter in a body, until the discovery of the atom and particle physi ...
and V the speed.
The angles are all assumed small, so the lateral force
In physics, a force is an influence that can cause an Physical object, object to change its velocity unless counterbalanced by other forces. In mechanics, force makes ideas like 'pushing' or 'pulling' mathematically precise. Because the Magnitu ...
equation is:
:
The rotation of the body subjected to a yawing moment N is governed by:
:
where I is the moment of inertia
The moment of inertia, otherwise known as the mass moment of inertia, angular/rotational mass, second moment of mass, or most accurately, rotational inertia, of a rigid body is defined relatively to a rotational axis. It is the ratio between ...
in yaw.
The forces and moments of interest arise from the distortion of the tyres. The angle between the direction the tread is rolling and the hub is called the slip angle. This is a bit of a misnomer, because the tyre as a whole does not actually slip, part of the region in contact with the road adheres, and part of the region slips. We assume that the tyre force is directly proportional to the slip angle (). This is made up of the slip of the vehicle as a whole modified by the angular velocity of the body. For the front axle:
:
whilst for the rear axle:
:
Let the constant of proportionality be k. The sideforce is, therefore:
:
The moment is:
:
Denoting the angular velocity , the equations of motion are:
:
:
:
Let (beta), the slip angle for the vehicle as a whole:
:
:
Eliminating yields the following equation in :
:
This is called a second-order linear homogeneous equation, and its properties form the basis of much of control theory
Control theory is a field of control engineering and applied mathematics that deals with the control system, control of dynamical systems in engineered processes and machines. The objective is to develop a model or algorithm governing the applic ...
.
Stability analysis
We do not need to solve the equation of motion explicitly to decide whether the solution diverges indefinitely or converges to zero following an initial perturbation. The form of the solution depends on the signs of the coefficients. The coefficient of will be called the ' damping' by analogy with a mass-spring-damper which has a similar equation of motion. By the same analogy, the coefficient of will be called the 'stiffness', as its function is to return the system to zero deflection, in the same manner as a spring. The form of the solution depends only on the signs of the damping and stiffness terms. The four possible solution types are presented in the figure. The only satisfactory solution requires both stiffness and damping to be positive. The damping term is: :: The tyre slip coefficient k is positive, as are the mass, moment of inertia and speed, so the damping is positive, and the directional motion should be dynamically stable. The stiffness term is: :: If the centre of gravity is ahead of the centre of thewheelbase
In both road and rail vehicles, the wheelbase is the horizontal distance between the centers of the front and rear wheels. For road vehicles with more than two axles (e.g. some trucks), the wheelbase is the distance between the steering (front ...
(, this will always be positive, and the vehicle will be stable at all speeds. However, if it lies further aft, the term has the potential of becoming negative above a speed given by:
::
Above this speed, the vehicle will be directionally unstable
In dynamical systems instability means that some of the outputs or internal state (controls), states increase with time, without bounds. Not all systems that are not Stability theory, stable are unstable; systems can also be marginal stability ...
.
Relative effect of front and rear tyres
If for some reason (incorrect inflation pressure, worn tread) the tyres on one axle are incapable of generating significant lateral force, the stability will obviously be affected. Assume to begin with that the rear tyres are faulty, what is the effect on stability? If the rear tyres produce no significant forces, the side force and yawing moment become: : : The equation of motion becomes: : The coefficient of is negative, so the vehicle will be unstable. Now consider the effect of faulty tyres at the front. The Side force and yawing moment become: : : The equation of motion becomes: : The coefficient of is positive, so the vehicle will be stable but unsteerable. It follows that the condition of the rear tyres is more critical to directional stability than the state of the front tyres. Also, locking the rear wheels by applying the handbrake, renders the vehicle directionally unstable, causing it to spin. Since the vehicle is not under control during the spin, the ' handbrake turn' is usually illegal on public roads.Steering forces
Deflecting the steering changes the slip angle of the front tyres, generating a sideforce. With conventional steering, the tyres are deflected by different amounts, but for the purposes of this analysis, the additional slip will be considered equal for both front tyres. The side force becomes: : where (eta) is the steering deflection. Similarly, the yawing moment becomes: : Including the steering term introduces a forced response: : The steady state response is with all time derivatives set to zero. Stability requires that the coefficient of must be positive, so the sign of the response is determined by the coefficient of : :: This is a function of speed. When the speed is low, the slip is negative and the body points out of the corner (itundersteer
Understeer and oversteer are vehicle dynamics terms used to describe the sensitivity of the vehicle to changes in steering angle associated with changes in lateral acceleration. This sensitivity is defined for a level road for a given steady state ...
s). At a speed given by:
::
The body points in the direction of motion. Above this speed, the body points into the corner (oversteer
Understeer and oversteer are vehicle dynamics terms used to describe the sensitivity of the vehicle to changes in steering angle associated with changes in lateral acceleration. This sensitivity is defined for a level road for a given steady state ...
s).
As an example:
::with k=10kN/radian, M=1000kg, b=1.0m, a=1.0m, the vehicle understeers below 11.3mph.
Evidently moving the centre of gravity forwards increases this speed, giving the vehicle a tendency to understeer
Understeer and oversteer are vehicle dynamics terms used to describe the sensitivity of the vehicle to changes in steering angle associated with changes in lateral acceleration. This sensitivity is defined for a level road for a given steady state ...
.
Note: Installing a heavy, powerful engine in a light weight production vehicle designed around a small engine increases both its directional stability, and its tendency to understeer. The result is an overpowered vehicle with poor cornering performance.
Even worse is the installation of an oversized power unit into a rear engined production vehicle without corresponding modification of suspension or mass distribution, as the result will be directionally unstable at high speed.
Limitations of the analysis
The forces arising from slip depend on the loading on the tyre as well as the slip angle, this effect has been ignored, but could be taken into account by assuming different values of k for the front and rear axles. Roll motion due to cornering will redistribute the tyre loads between the nearside and offside of the vehicle, again modifying the tyre forces. Engine torque likewise re-distributes the load between front and rear tyres. A full analysis should also take account of the suspension response. The complete analysis is essential for the design of high performance road vehicles, but is beyond the scope of this article.Aviation
 Directional stability about the aircraft's vertical axis is also referred to as yawing. This is primarily achieved by the area of the
Directional stability about the aircraft's vertical axis is also referred to as yawing. This is primarily achieved by the area of the vertical stabilizer
A vertical stabilizer or tail fin is the static part of the vertical tail of an aircraft. The term is commonly applied to the assembly of both this fixed surface and one or more movable rudders hinged to it. Their role is to provide control, sta ...
and the sides of the fuselage aft of the center of gravity. When an airplane is flying in a straight line while hit by a side gust of wind, the left/right yawing motion will be stopped by the air striking at the right/left side of the vertical stabilizer.
See also
*Relaxed stability
In aviation, an aircraft is said to have relaxed stability if it has low or negative stability.
An aircraft with negative stability will have a tendency to change its pitch and bank angles spontaneously. An aircraft with negative stability cann ...
*Car handling
Automobile handling and vehicle handling are descriptions of the way a wheeled vehicle responds and reacts to the inputs of a driver, as well as how it moves along a track or road. It is commonly judged by how a vehicle performs particularly duri ...
*Flight dynamics
Flight dynamics in aviation and spacecraft, is the study of the performance, stability, and control of vehicles flight, flying through the air or in outer space. It is concerned with how forces acting on the vehicle determine its velocity and at ...
* Dutch roll
*Longitudinal stability
In flight dynamics, longitudinal stability is the Flight dynamics (fixed-wing aircraft), stability of an aircraft in the longitudinal, or Aircraft principal axes, pitching, plane. This characteristic is important in determining whether an aircraft ...
* Hunting oscillation
References
Further reading
* Barwell F T: Automation and Control in Transport, Pergamon Press, 1972. * Synge J L and B A Griffiths: Principles of Mechanics, Section 6.3, McGraw-Hill Kogakusha Ltd,3rd Edition, 1970.External links
*{{Commons category-inline, Directional stability Mechanics